文章目录
- 08 后端 1
- 8.1 概述
- 8.1.1 状态估计的概率解释
- 8.1.2 线性系统和卡尔曼滤波(KF)
- 8.1.3 非线性系统和扩展卡尔曼滤波(EKF)
- 8.1.4 小结
08 后端 1
前端视觉里程计可以给出一个短时间内的轨迹和地图,但由于不可避免的误差积累,地图在长时间内是不准确的,因此,我们希望构建一个大规模、长时间的最优轨迹和地图。
8.1 概述
8.1.1 状态估计的概率解释
(1)两种处理方式
-
批量式:使用过去和未来的信息来更新自己的状态的处理方式;
-
渐进式:仅适用过去的甚至仅是前一个时刻的信息来更新自己的状态的处理方式。
(2)运动方程和观测方程:
{ x k = f ( x k − 1 , u k ) + w k z k , j = h ( y j , x k ) + v k , j k = 1 , … , N , j = 1 , … , M (8-1) \left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k, j}=h\left(\boldsymbol{y}_{j}, \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k, j} \end{array} \quad k=1, \ldots, N, j=1, \ldots, M\right. \tag{8-1} {xk=f(xk−1,uk)+wkzk,j=h(yj,xk)+vk,jk=1,…,N,j=1,…,M(8-1)
以下图为例,只有运动方程时,由于误差的不断积累,位置的不确定性会不断增大;当加入正确的观测数据,不确定性就会减小,直至保持稳定。
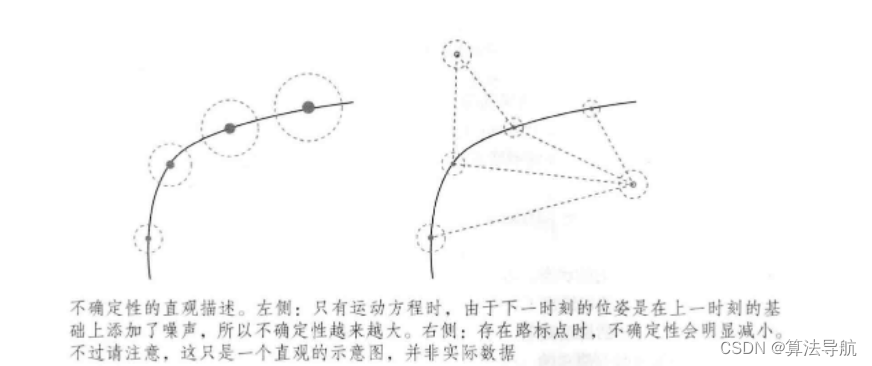
(3)将批量状态估计问题转化为最大似然估计问题,并使用最小二乘法求解。
定义 x k \boldsymbol{x}_k xk 为 k k k 时刻的所有变量,即包含此时刻的相机位姿和 m m m 个路标,
x k = def { x k , y 1 , … , y m } \boldsymbol{x}_{k} \stackrel{\text { def }}{=}\left\{\boldsymbol{x}_{k}, \boldsymbol{y}_{1}, \ldots, \boldsymbol{y}_{m}\right\} xk= def {xk,y1,…,ym}
同时,把 k k k 时刻所有的观测记做 z k \boldsymbol{z}_k zk,于是式(8-1)可写为(注意区别)
{ x k = f ( x k − 1 , u k ) + w k z k = h ( x k ) + v k k = 1 , … , N (8-2) \left\{\begin{array}{l} \boldsymbol{x}_{k}=f\left(\boldsymbol{x}_{k-1}, \boldsymbol{u}_{k}\right)+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=h\left( \boldsymbol{x}_{k}\right)+\boldsymbol{v}_{k} \end{array} \quad k=1, \ldots, N\right. \tag{8-2} {xk=f(xk−1,uk)+wkzk=h(xk)+vkk=1,…,N(8-2)
我们希望用过去 0 到第 k k k 时刻所有的数据来估计现在的状态分布:
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) P(\boldsymbol{x}_k|\boldsymbol{x}_0,\boldsymbol{u}_{1:k},\boldsymbol{z}_{1:k}) P(xk∣x0,u1:k,z1:k)
下标 1 : k 1:k 1:k 表示从 1 到 k k k 时刻所有的数据。
根据贝叶斯法则
P ( x k ∣ x 0 , u 1 : k , z 1 : k ) ∝ P ( z k ∣ x k ) P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) (8-3) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k}\right) \propto P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) \tag{8-3} P(xk∣x0,u1:k,z1:k)∝P(zk∣xk)P(xk∣x0,u1:k,z1:k−1)(8-3)
第一项称为 似然,第二项为 先验,将第二项以 x k − 1 \boldsymbol{x}_{k-1} xk−1 时刻为条件概率展开
P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = ∫ P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) d x k − 1 (8-4) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=\int P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) \mathrm{d} \boldsymbol{x}_{k-1} \tag{8-4} P(xk∣x0,u1:k,z1:k−1)=∫P(xk∣xk−1,x0,u1:k,z1:k−1)P(xk−1∣x0,u1:k,z1:k−1)dxk−1(8-4)
(可以这样理解,第一项表示 k k k 时刻状态和 k − 1 k-1 k−1 时刻有关,第二项表示 k − 1 k-1 k−1 时刻状态又与过去所有状态有关,这是一个递进的关系。)
在后续处理上,又有两种方式:一种是假设一阶马尔科夫性,即 k k k 时刻的状态只与 k − 1 k-1 k−1 时刻状态相关,这样就会得到以 扩展卡尔曼滤波 为代表的滤波器法;另一种是与之前所有的状态均相关,将得到 非线性优化 为主体的优化框架。目前,视觉 SLAM 的主流为非线性优化方法。
8.1.2 线性系统和卡尔曼滤波(KF)
(1)假设马尔可夫性,即当前时刻状态只与前一时刻的状态有关。则式(8-4)第一项可写为
P ( x k ∣ x k − 1 , x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k ∣ x k − 1 , u k ) (8-5) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1}, \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right) = P(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{k-1},\boldsymbol{u}_k) \tag{8-5} P(xk∣xk−1,x0,u1:k,z1:k−1)=P(xk∣xk−1,uk)(8-5)
对于第二项,由于 k k k 时刻的输入量 u k \boldsymbol{u}_k uk 与 k − 1 k-1 k−1 时刻状态无关,则可将其化简为
P ( x k − 1 ∣ x 0 , u 1 : k , z 1 : k − 1 ) = P ( x k − 1 ∣ x 0 , u 1 : k − 1 , z 1 : k − 1 ) (8-6) P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=P\left(\boldsymbol{x}_{k-1} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k-1}, \boldsymbol{z}_{1: k-1}\right) \tag{8-6} P(xk−1∣x0,u1:k,z1:k−1)=P(xk−1∣x0,u1:k−1,z1:k−1)(8-6)
(2)首先推导 线性高斯系统 的卡尔曼滤波器(也就是说,运动方程和观测方程可以由线性方程来描述):
{ x k = A k x k − 1 + u k + w k z k = C k x k + v k k = 1 , … , N (8-8) \left\{\begin{array}{l} \boldsymbol{x}_{k}=\boldsymbol{A}_{k} \boldsymbol{x}_{k-1}+\boldsymbol{u}_{k}+\boldsymbol{w}_{k} \\ \boldsymbol{z}_{k}=\boldsymbol{C}_{k} \boldsymbol{x}_{k}+\boldsymbol{v}_{k} \end{array} \quad k=1, \ldots, N\right. \tag{8-8} {xk=Akxk−1+uk+wkzk=Ckxk+vkk=1,…,N(8-8)
假设噪声符合零均值高斯分布,即
w k ∼ N ( 0 , R ) . v k ∼ N ( 0 , Q ) (8-9) \boldsymbol{w}_{k} \sim N(\mathbf{0}, \boldsymbol{R}) . \quad \boldsymbol{v}_{k} \sim N(\mathbf{0}, \boldsymbol{Q}) \tag{8-9} wk∼N(0,R).vk∼N(0,Q)(8-9)
假设已知 k − 1 k-1 k−1 时刻的后验状态估计 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 及其协方差 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1,现在根据 k k k 时刻的输入和观测数据,确定 x k \boldsymbol{x}_k xk 的后验分布。我们约定以上帽子 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 表示后验,下帽子 x ˇ k \check{\boldsymbol{x}}_{k} xˇk 表示先验分布。
根据 高斯分布线性组合性质,先通过运动方程确定 x k \boldsymbol{x}_k xk 的先验分布
P ( x k ∣ x 0 , u 1 : k , z 1 : k − 1 ) = N ( A k x ^ k − 1 + u k , A k P ^ k − 1 A k T + R ) (8-10) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{1: k-1}\right)=N(\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R}) \tag{8-10} P(xk∣x0,u1:k,z1:k−1)=N(Akx^k−1+uk,AkP^k−1AkT+R)(8-10)
这一步称为 预测 ,它显示了如何从上一时刻的状态,根据输入信息推断当前时刻的状态分布。这个分布就是 先验,记
x k ˇ = A k x ^ k − 1 + u k , P ˇ k = A k P ^ k − 1 A k T + R (8-11) \check{\boldsymbol{x}_k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R} \tag{8-11} xkˇ=Akx^k−1+uk,Pˇk=AkP^k−1AkT+R(8-11)
由观测方程,我们可以计算在某个状态下应该产生怎样的观测数据,
P ( z k ∣ x k ) = N ( C k x k , Q ) ) (8-12) P(\boldsymbol{z}_k|\boldsymbol{x}_k)=N(\boldsymbol{C}_{k} \boldsymbol{x}_{k},\boldsymbol{Q})) \tag{8-12} P(zk∣xk)=N(Ckxk,Q))(8-12)
为了得到 x k \boldsymbol{x}_k xk 的后验概率,我们需要计算它们的乘积,也就是式(8-3)。设最终的结果为 x k ∼ N ( x ^ k , P ^ k ) \boldsymbol{x}_k \sim N(\hat{\boldsymbol{x}}_k, \hat{\boldsymbol{P}}_k) xk∼N(x^k,P^k) ,则
N ( x ^ k , P ^ k ) = η N ( C k x k , Q ) ) ⋅ N ( x ˇ k , P ˇ k ) (8-13) N(\hat{\boldsymbol{x}}_k, \hat{\boldsymbol{P}}_k)=\eta N(\boldsymbol{C}_{k} \boldsymbol{x}_{k},\boldsymbol{Q})) \cdot N(\check{\boldsymbol{x}}_k, \check{\boldsymbol{P}}_k) \tag{8-13} N(x^k,P^k)=ηN(Ckxk,Q))⋅N(xˇk,Pˇk)(8-13)
我们知道高维高斯分布的概率密度函数为
p ( x ) = 1 ( 2 π ) N det ( Σ ) exp ( − 1 2 ( x − μ ) T Σ − 1 ( x − μ ) ) p(x)=\frac{1}{\sqrt{(2 \pi)^{N} \operatorname{det}(\boldsymbol{\Sigma})}} \exp \left(-\frac{1}{2}(\boldsymbol{x}-\boldsymbol{\mu})^{\mathrm{T}} \boldsymbol{\Sigma}^{-1}(\boldsymbol{x}-\boldsymbol{\mu})\right) p(x)=(2π)Ndet(Σ)1exp(−21(x−μ)TΣ−1(x−μ))
因此,将指数部分展开
( x k − x ^ k ) T P ^ k − 1 ( x k − x ^ k ) = ( z k − C k x k ) T Q − 1 ( z k − C k x k ) + ( x k − x ˇ k ) T P ˇ k − 1 ( x k − x ˇ k ) (8-14) (\boldsymbol{x}_k-\hat{\boldsymbol{x}}_k)^\mathrm{T}\hat{\boldsymbol{P}}_k^{-1}(\boldsymbol{x}_k-\hat{\boldsymbol{x}}_k)=\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)^{\mathrm{T}} \boldsymbol{Q}^{-1}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \boldsymbol{x}_{k}\right)+\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right) \tag{8-14} (xk−x^k)TP^k−1(xk−x^k)=(zk−Ckxk)TQ−1(zk−Ckxk)+(xk−xˇk)TPˇk−1(xk−xˇk)(8-14)
为了求左侧的 x ^ k \hat{\boldsymbol{x}}_k x^k 和 P ^ k \hat{\boldsymbol{P}}_k P^k ,将两侧展开,并比较一次和二次项系数。对于二次系数
P ^ k − 1 = C k T Q − 1 C k + P ˇ k − 1 (8-15) \hat{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k}+\check{\boldsymbol{P}}_{k}^{-1} \tag{8-15} P^k−1=CkTQ−1Ck+Pˇk−1(8-15)
该式给出了协方差的计算过程。这里定义一个中间变量
K = P ^ k C k T Q − 1 (8-16) \boldsymbol{K}=\hat{\boldsymbol{P}}_{k}\boldsymbol{C}_{k}^{\mathrm{T}}\boldsymbol{Q}^{-1} \tag{8-16} K=P^kCkTQ−1(8-16)
将式(8-15)两侧时左乘乘 P ^ k \hat{\boldsymbol{P}}_{k} P^k,得
I = P ^ k C k T Q − 1 C k + P ^ k P ˇ k − 1 = K C k + P ^ k P ˇ k − 1 (8-17) \boldsymbol{I}=\hat{\boldsymbol{P}}_{k}\boldsymbol{C}_{k}^{\mathrm{T}}\boldsymbol{Q}^{-1}\boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k}\check{\boldsymbol{P}}_{k}^{-1}=\boldsymbol{K}\boldsymbol{C}_{k}+\hat{\boldsymbol{P}}_{k}\check{\boldsymbol{P}}_{k}^{-1} \tag{8-17} I=P^kCkTQ−1Ck+P^kPˇk−1=KCk+P^kPˇk−1(8-17)
于是,得
P ^ k = ( I − K C k ) P ˇ k (8-18) \hat{\boldsymbol{P}}_{k}=(\boldsymbol{I}-\boldsymbol{K}\boldsymbol{C}_{k})\check{\boldsymbol{P}}_{k} \tag{8-18} P^k=(I−KCk)Pˇk(8-18)
然后比较一次项的系数
− 2 x ^ k T P ^ k − 1 x k = − 2 z k T Q − 1 C k x k − 2 x ˇ k T P ˇ k − 1 x k (8-19) -2 \hat{\boldsymbol{x}}_{k}^{\mathrm{T}} \hat{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k}=-2 \boldsymbol{z}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{C}_{k} \boldsymbol{x}_{k}-2 \check{\boldsymbol{x}}_{k}^{\mathrm{T}} \check{\boldsymbol{P}}_{k}^{-1} \boldsymbol{x}_{k} \tag{8-19} −2x^kTP^k−1xk=−2zkTQ−1Ckxk−2xˇkTPˇk−1xk(8-19)
整理,得
P ^ k − 1 x ^ k = C k T Q − 1 z k + P ˇ k − 1 x ˇ k (8-20) \hat{\boldsymbol{P}}_{k}^{-1} \hat{\boldsymbol{x}}_{k}=\boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \tag{8-20} P^k−1x^k=CkTQ−1zk+Pˇk−1xˇk(8-20)
两侧同时左乘 P ^ k \hat{\boldsymbol{P}}_{k} P^k,并代入式(8-16)
x ^ k = P ^ k C k T Q − 1 z k + P ^ k P ˇ k − 1 x ˇ k = K z k + ( I − K C k ) x ˇ k = x ˇ k + K ( z k − C k x ˇ k ) (8-21) \begin{aligned} \hat{\boldsymbol{x}}_{k} &=\hat{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}} \boldsymbol{Q}^{-1} \boldsymbol{z}_{k}+\hat{\boldsymbol{P}}_{k} \check{\boldsymbol{P}}_{k}^{-1} \check{\boldsymbol{x}}_{k} \\ &=\boldsymbol{K} \boldsymbol{z}_{k}+\left(\boldsymbol{I}-\boldsymbol{K} \boldsymbol{C}_{k}\right) \check{\boldsymbol{x}}_{k}=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right) \end{aligned} \tag{8-21} x^k=P^kCkTQ−1zk+P^kPˇk−1xˇk=Kzk+(I−KCk)xˇk=xˇk+K(zk−Ckxˇk)(8-21)
至此,我们得到了后验协方差 P ^ k \hat{\boldsymbol{P}}_{k} P^k(式(8-15))和均值 x ^ k \hat{\boldsymbol{x}}_{k} x^k (式8-21)的表达式。
(3)线性卡尔曼滤波可归纳为 预测 和 更新 两个步骤:
——————————————————————————————————————————————————————————
① 预测:
x k ˇ = A k x ^ k − 1 + u k , P ˇ k = A k P ^ k − 1 A k T + R \check{\boldsymbol{x}_k}=\boldsymbol{A}_{k} \hat{\boldsymbol{x}}_{k-1}+\boldsymbol{u}_{k}, \quad \check{\boldsymbol{P}}_{k}=\boldsymbol{A}_{k} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{A}_{k}^{\mathrm{T}}+\boldsymbol{R} xkˇ=Akx^k−1+uk,Pˇk=AkP^k−1AkT+R
② 更新:先计算卡尔曼增益 K \boldsymbol{K} K(这与前面 定义的 K \boldsymbol{K} K 形式有所差别,但实际上是等价的 )
K = P ˇ k C k T ( C k P ˇ k C k T + Q k ) − 1 \boldsymbol{K}=\check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}\left(\boldsymbol{C}_{k} \check{\boldsymbol{P}}_{k} \boldsymbol{C}_{k}^{\mathrm{T}}+\boldsymbol{Q}_{k}\right)^{-1} K=PˇkCkT(CkPˇkCkT+Qk)−1
再计算后验概率分布
x ^ k = x ˇ k + K ( z k − C k x ˇ k ) P ^ k = ( I − K C k ) P ˇ k \begin{aligned} \hat{\boldsymbol{x}}_{k}&=\check{\boldsymbol{x}}_{k}+\boldsymbol{K}\left(\boldsymbol{z}_{k}-\boldsymbol{C}_{k} \check{\boldsymbol{x}}_{k}\right) \\ \hat{\boldsymbol{P}}_{k}&=(\boldsymbol{I}-\boldsymbol{K}\boldsymbol{C}_{k})\check{\boldsymbol{P}}_{k} \end{aligned} x^kP^k=xˇk+K(zk−Ckxˇk)=(I−KCk)Pˇk
——————————————————————————————————————————————————————————
这就是经典卡尔曼滤波中的五个公式。事实上,卡尔曼滤波还有其他的表达形式。
8.1.3 非线性系统和扩展卡尔曼滤波(EKF)
实际上,SLAM 中的运动方程和观测方程都是非线性的,而高斯分布经过非线性变换,其结果往往也不再是高斯分布。因此,在非线性系统中,必须取一定的近似,将非高斯分布近似为高斯分布。
(1)我们希望将上面的线性卡尔曼滤波器扩展到非线性系统中。即在某点附近,将运动方程和观测方程一阶泰勒展开,只保留一阶项(线性部分),然后按照线性系统进行推导。
假设 k − 1 k-1 k−1 时刻的均值和协方差矩阵为 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 和 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1,在 k k k 时刻,把运动方程和观测方程在 x ^ k − 1 \hat{\boldsymbol{x}}_{k-1} x^k−1 、 P ^ k − 1 \hat{\boldsymbol{P}}_{k-1} P^k−1 处一阶展开,有
x k ≈ f ( x ^ k − 1 , u k ) + ∂ f ∂ x k − 1 ∣ x ^ k − 1 ( x k − 1 − x ^ k − 1 ) + w k (8-22) \boldsymbol{x}_{k} \approx f\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}\right)+\left.\frac{\partial f}{\partial \boldsymbol{x}_{k-1}}\right|_{\hat{\boldsymbol{x}}_{k-1}}\left(\boldsymbol{x}_{k-1}-\hat{\boldsymbol{x}}_{k-1}\right)+\boldsymbol{w}_{k} \tag{8-22} xk≈f(x^k−1,uk)+∂xk−1∂f x^k−1(xk−1−x^k−1)+wk(8-22)
记
F = ∂ f ∂ x k − 1 ∣ x ^ k − 1 (8-23) \boldsymbol{F}=\left.\frac{\partial f}{\partial \boldsymbol{x}_{k-1}}\right|_{\hat{\boldsymbol{x}}_{k-1}} \tag{8-23} F=∂xk−1∂f x^k−1(8-23)
同样,对观测方程,在 x k \boldsymbol{x}_k xk 处展开
z k ≈ h ( x ˇ ) + ∂ h ∂ x k ∣ x ˇ k ( x k − x ˇ k ) + n k (8-24) \boldsymbol{z}_{k} \approx h\left(\check{\boldsymbol{x}}\right)+\left.\frac{\partial h}{\partial \boldsymbol{x}_{k}}\right|_{\check{\boldsymbol{x}}_{k}}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right)+\boldsymbol{n}_{k} \tag{8-24} zk≈h(xˇ)+∂xk∂h xˇk(xk−xˇk)+nk(8-24)
记
H = ∂ h ∂ x k ∣ x ˇ k (8-25) \boldsymbol{H}=\left.\frac{\partial h}{\partial \boldsymbol{x}_{k}}\right|_{\check{\boldsymbol{x}}_{k}} \tag{8-25} H=∂xk∂h xˇk(8-25)
类似式(8-10),根据运动方程得到 x k \boldsymbol{x}_k xk 的先验分布
P ( x k ∣ x 0 , u 1 : k , z 0 : k − 1 ) = N ( f ( x ^ k − 1 , u k ) , F P ^ k − 1 F T + R k ) (8-26) P\left(\boldsymbol{x}_{k} \mid \boldsymbol{x}_{0}, \boldsymbol{u}_{1: k}, \boldsymbol{z}_{0: k-1}\right)=N(f\left(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}\right), \boldsymbol{F} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{R}_k) \tag{8-26} P(xk∣x0,u1:k,z0:k−1)=N(f(x^k−1,uk),FP^k−1FT+Rk)(8-26)
记先验的均值和协方差为
x ˇ k = f ( x ^ k − 1 , u k ) , P ˇ k = F P ^ k − 1 F T + R k (8-27) \check{\boldsymbol{x}}_k=f(\hat{\boldsymbol{x}}_{k-1}, \boldsymbol{u}_{k}), \quad \check{\boldsymbol{P}}_k=\boldsymbol{F} \hat{\boldsymbol{P}}_{k-1} \boldsymbol{F}^{\mathrm{T}}+\boldsymbol{R}_k \tag{8-27} xˇk=f(x^k−1,uk),Pˇk=FP^k−1FT+Rk(8-27)
在观测中,有
P ( z k ∣ x k ) = N ( h ( x ˇ ) + H ( x k − x ˇ k ) , Q k ) (8-28) P\left(\boldsymbol{z}_{k} \mid \boldsymbol{x}_{k}\right)=N(h\left(\check{\boldsymbol{x}}\right)+\boldsymbol{H}\left(\boldsymbol{x}_{k}-\check{\boldsymbol{x}}_{k}\right), \boldsymbol{Q}_k) \tag{8-28} P(zk∣xk)=N(h(xˇ)+H(xk−xˇk),Qk)(8-28)
类似线性卡尔曼滤波,定义增益 K k \boldsymbol{K}_k Kk
K k = P k ˇ H T ( H P k ˇ H T + Q k ) ) − 1 (8-29) \boldsymbol{K}_k=\check{\boldsymbol{P}_k}\boldsymbol{H}^\mathrm{T}(\boldsymbol{H}\check{\boldsymbol{P}_k}\boldsymbol{H}^\mathrm{T}+\boldsymbol{Q}_k))^{-1} \tag{8-29} Kk=PkˇHT(HPkˇHT+Qk))−1(8-29)
那么, x k \boldsymbol{x}_k xk 的后验概率分布为
x ^ k = x ˇ k + K k ( z k − h ( x ˇ k ) ) , P ^ k = ( I − K k H ) P ˇ k (8-29) \hat{\boldsymbol{x}}_k=\check{\boldsymbol{x}}_k+\boldsymbol{K}_k(z_k-h(\check{\boldsymbol{x}}_k)), \quad \hat{\boldsymbol{P}}_k=(\boldsymbol{I}-\boldsymbol{K}_k\boldsymbol{H})\check{\boldsymbol{P}}_k \tag{8-29} x^k=xˇk+Kk(zk−h(xˇk)),P^k=(I−KkH)Pˇk(8-29)
8.1.4 小结
EKF 的优点:
-
推导简单,适用于各种形式传感器;
-
易做多传感器融合。
EKF 的缺点
-
一阶马尔科夫性过于简单;
-
可能会发散;
-
线性化误差;
-
从程序实现上来说,需要储存所有状态量的均值和方差,不适用于大型场景。