前言: 最近项目需要对公司未来业绩进行预测,以便优化决策,so 研究一下时序算法。纯个人理解,记录以便备用(只探究一下原理,所有算法都使用基本状态,并未进行特征及参数优化)。
环境: python3.10 + jupyter
文章目录
- 1、时间序列基本概念
- 2、数据准备
- 2.1 相关库导入
- 2.2 数据获取
- 2.3 选取本次测试数据(2号商店、0类产品数据)
- 3、模型测试
- 3.1 传统时序建模
- 3.1.1 平稳性检验(单位根检验)+ 差分预处理
- 3.1.2 自相关acf(auto-correlation function) 和偏自相关pacf(partial auto-correlation function) 图
- 3.1.3 自相关 和 偏自相关 说明的问题
- 3.1.4 ARIMA模型:
- 3.2 机器学习模型
- 3.2.1 LR (线性回归)
- 3.2.2 Xgboost
1、时间序列基本概念
时间序列:是在连续等间隔时间点(秒、分、天、月等)上所获取的同一观察对象的状态值的序列。
一般组成:
1. 趋势性:随着时间的发展和变化,观测值呈现一种比较缓慢而长期的持续上升或下降的趋势。
2. 季节性:观测值随着自然季节的交替出现高峰与波谷的规律。
3. 周期性:观测值受产品特性或市场规律周期性变动,不随季节变化。
4. 随机性:个别随机噪声。
平稳性:从统计学的角度来看,平稳性是指数据的分布在时间上平移时不发生变化(均值和方差几乎不变)。
白噪声:均值为0的平稳序列,随机噪声,频谱类似白光光谱,故称白噪声。
差分:目的让序列变平稳
设函数 y t = f ( t ) 在 t = 0 , 1 , 2 , 3... 处有定义,对应的函数值为 y 0 , y 1 , y 2 , y 3 . . . , 则函数 y t = f ( t ) 在 t 处的一阶差分定义为: △ y t = y t + 1 − y t = f t + 1 − f t 设函数y_t=f(t)在t=0,1,2,3...处有定义,对应的函数值为y_0,y_1,y_2,y_3... ,则函数y_t=f(t)在t处的一阶差分定义为:\\ \triangle y_t=y_{t+1}-y_t=f_{t+1}-f_t 设函数yt=f(t)在t=0,1,2,3...处有定义,对应的函数值为y0,y1,y2,y3...,则函数yt=f(t)在t处的一阶差分定义为:△yt=yt+1−yt=ft+1−ft
2、数据准备
2.1 相关库导入
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import random
import arrow# 编码
from category_encoders import TargetEncoder# 传统统计模型
import statsmodels.tsa.api as sm
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from statsmodels.tsa.stattools import adfuller# 机器学习模型
from sklearn.linear_model import Ridge,LinearRegression
from sklearn.preprocessing import OneHotEncoder,MaxAbsScaler
import xgboost as xgb# 深度学习
import torch
import torch.nn as nn
from torch.nn import L1Loss,MSELoss
from torch.optim import SGD,Adam
from torch.utils.data import Dataset,DataLoaderimport warningswarnings.filterwarnings('ignore')sns.set_theme(style='darkgrid',font='Microsoft YaHei')
2.2 数据获取
kaggle 时序数据集 https://www.kaggle.com/datasets/samuelcortinhas/time-series-practice-dataset
该数据集包含不同商店下不同产品2010-2020年10年的销量数据。(应该是人造数据)
# 1. 数据集探索
data = pd.read_csv('./data/train.csv',parse_dates=['Date'])
store = data['store'].unique() # 商店编号
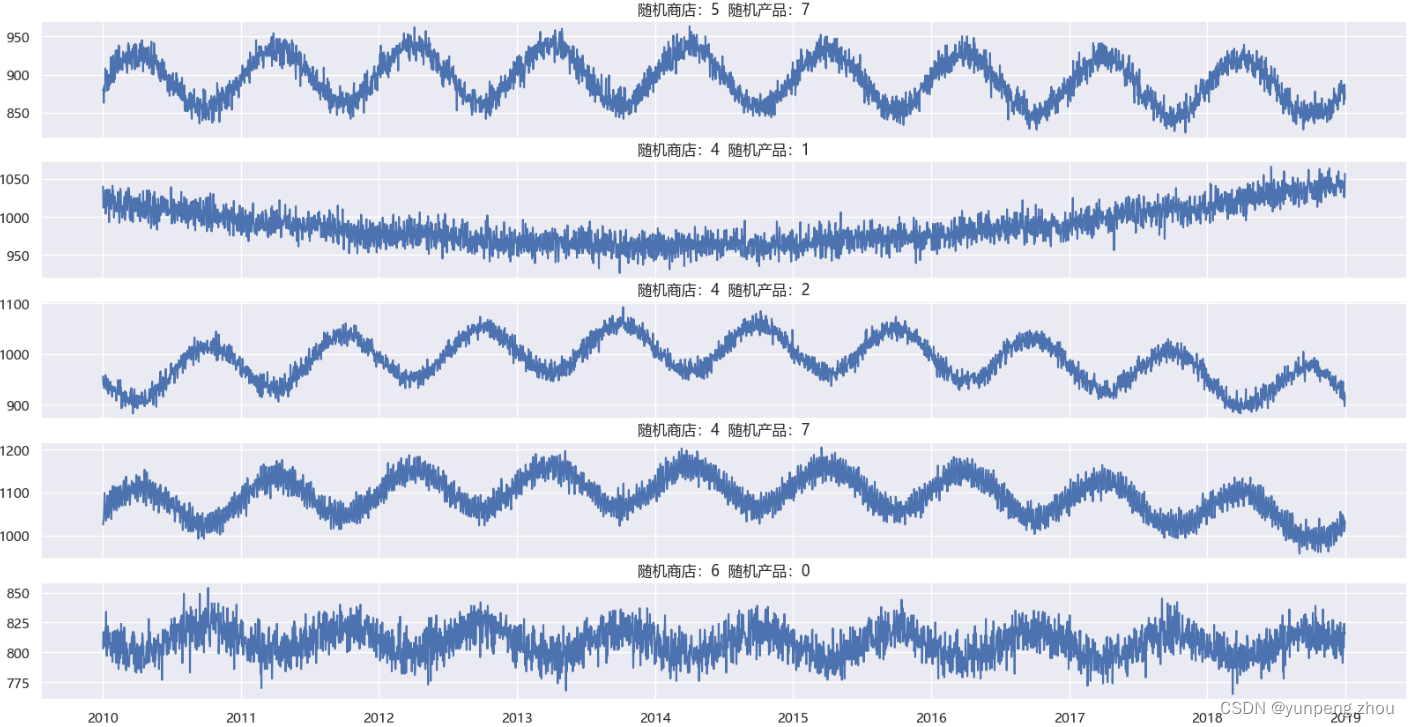
product = data['product'].unique() # 产品编号# 2. 展示随机商店、随机产品时序图
fg,axes = plt.subplots(nrows=5,ncols=1,sharex=True)
for ax in axes:store_selected = random.choice(store)product_selected = random.choice(product)ax.plot(data.query(f'store == {store_selected} & product == {product_selected}')['Date'],data.query(f'store == {store_selected} & product == {product_selected}')['number_sold'])ax.set_title(f'随机商店:{store_selected} 随机产品:{product_selected}')
fg.set_size_inches(20,10)
2.3 选取本次测试数据(2号商店、0类产品数据)
# 1. 选取测试时序数据
store = 2
product = 0
data_train = pd.read_csv('./data/train.csv',parse_dates=['Date']).query(f'store == {store} & product == {product}')[['Date','number_sold']] # 训练集
data_test = pd.read_csv('./data/test.csv',parse_dates=['Date']).query(f'store == {store} & product == {product}')[['Date','number_sold']] # 测试集# 2. 训练集与测试集整体状态
plt.subplot(3,1,1)
plt.plot(data_train['Date'],data_train['number_sold'],label='观测值')
plt.plot(data_test['Date'],data_test['number_sold'],label='待预估值')
plt.title('trend + seasonal Time Series')
plt.legend()# 2.2 查看年中规律
plt.subplot(3,1,2)
year = random.choice(range(2010,2019)) # 随机选取年
year_selected = f'Date >= "{year}-01-01" & Date <= "{year}-12-31"'
plt.plot(data_train.query(year_selected)['Date'],data_train.query(year_selected)['number_sold'],label='观测值')
plt.title('随机选取其中一年查看其它规律')
plt.legend()# 2.3 查看月中规律
plt.subplot(3,1,3)
month = random.choice(range(1,13)) # 随机选取月
month_start = f"{year}-{month:0>2}-01"
month_end = arrow.get(month_start).ceil('month').date()
month_select = f'Date >= "{month_start}" & Date <= "{month_end}"'
plt.plot(data_train.query(month_select)['Date'],data_train.query(month_select)['number_sold'],label='观测值')
plt.title('随机选取其中一月查看其它规律')
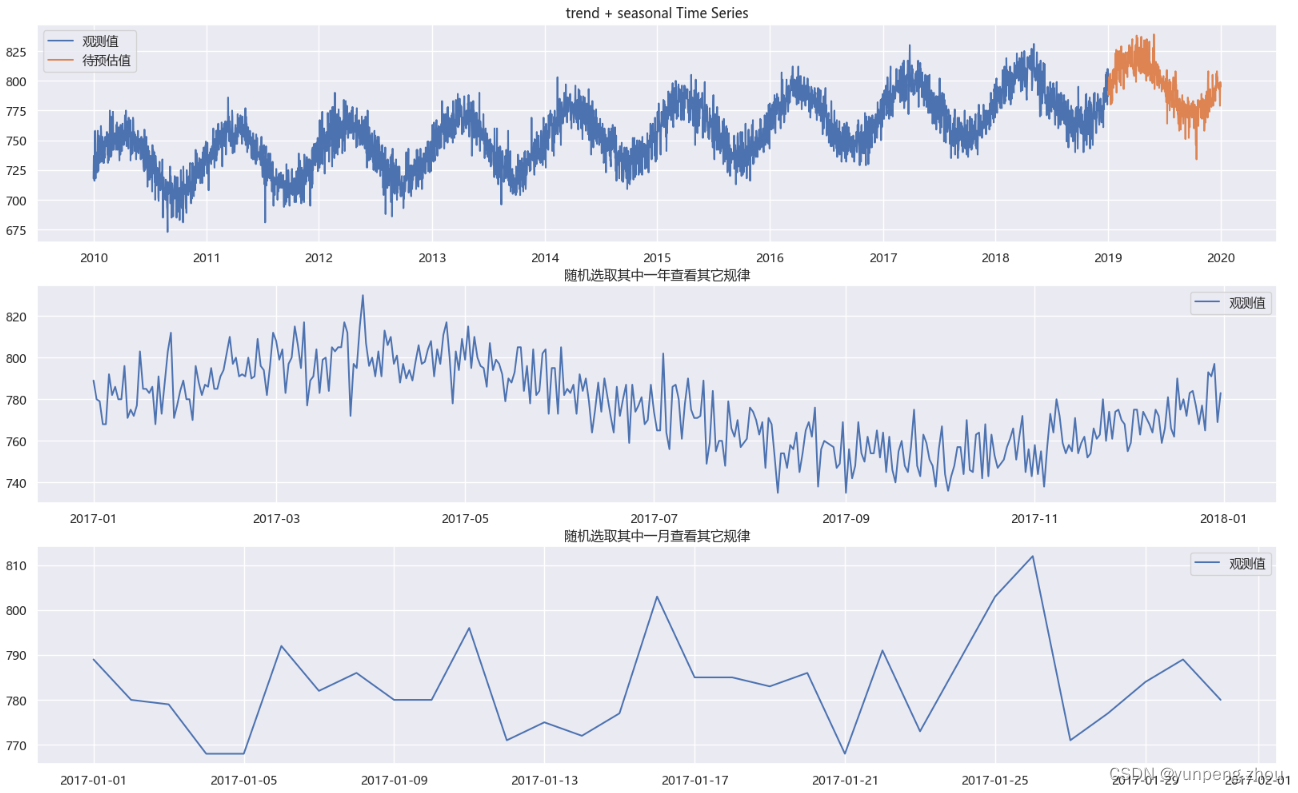
plt.legend()plt.gcf().set_size_inches(20,12)
如图:该序列具有增长趋势和年季节性特性,无明显节假日和week特性。
3、模型测试
3.1 传统时序建模
3.1.1 平稳性检验(单位根检验)+ 差分预处理
# 1. 差分
data_train['number_sold_diff'] = data_train['number_sold'].diff(1)# 2. 季节差分
data_train['number_sold_season_diff'] = data_train['number_sold'].diff(365)# 3. 差分 + 季节差分
data_train['number_sold_diff_season'] = data_train['number_sold_diff'].diff(365)# 4. 删除差分后空值
data_train.dropna(inplace=True)# 5.单位根检验(原假设:该序列为非平稳序列)
origin_pvalue = adfuller(data_train['number_sold'])[1]
diff_pvalue = adfuller(data_train['number_sold_diff'])[1]
season_diff_pvalue = adfuller(data_train['number_sold_season_diff'])[1]
diff_and_season_diff_pvalue = adfuller(data_train['number_sold_diff_season'])[1]# 6. 绘制各种差分后序列图
plt.subplot(3,1,1)
plt.plot(data_train['Date'],data_train['number_sold_diff'])
plt.title(f'一阶差分,;单位根检验p值:{diff_pvalue}')
plt.subplot(3,1,2)
plt.plot(data_train['Date'],data_train['number_sold_season_diff'])
plt.title(f'季节差分;单位根检验p值:{season_diff_pvalue}')
plt.subplot(3,1,3)
plt.plot(data_train['Date'],data_train['number_sold_diff_season'])
plt.title(f'一阶差分 + 一阶季节差分;单位根检验p值:{season_diff_pvalue}')
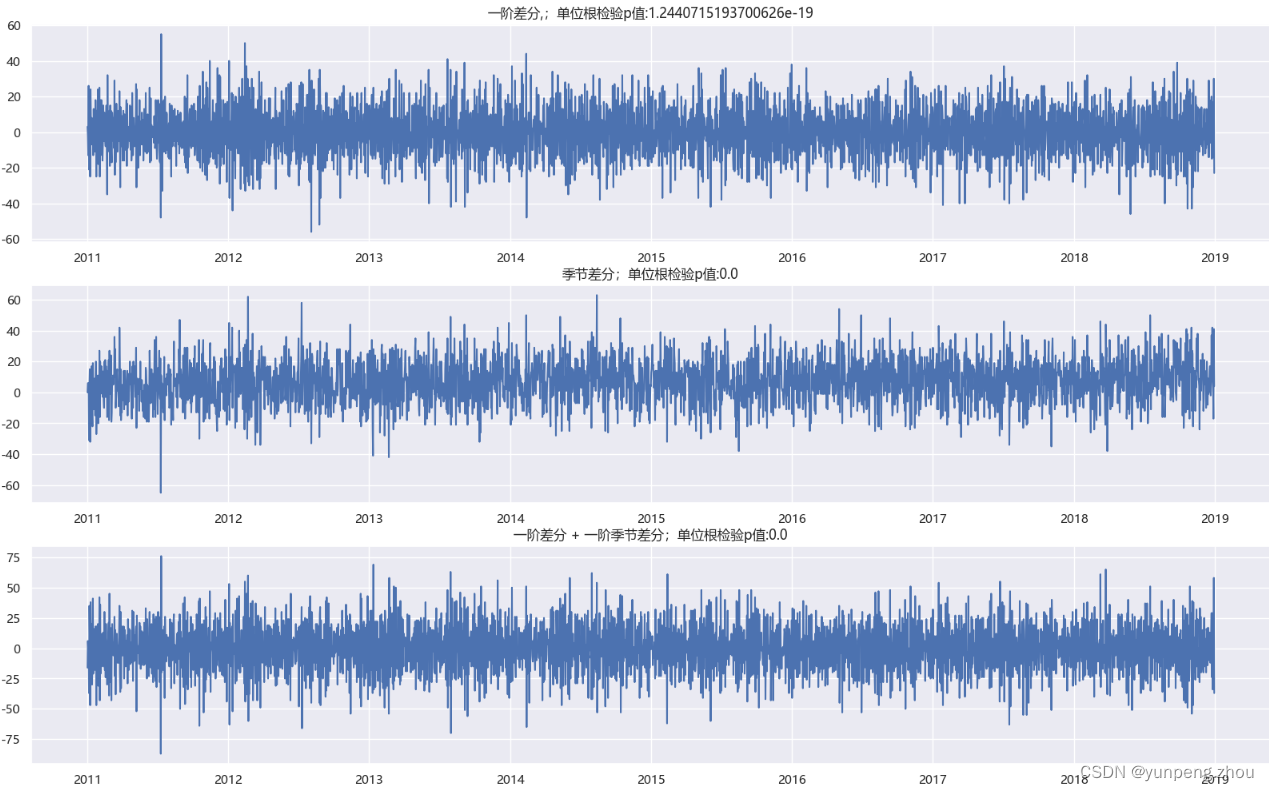
plt.gcf().set_size_inches(20,12)如图:一阶差分、季节差分、一阶差分 + 一阶季节差分 3种差分后单位根检验p值都接近于0,差分后均为平稳序列
3.1.2 自相关acf(auto-correlation function) 和偏自相关pacf(partial auto-correlation function) 图
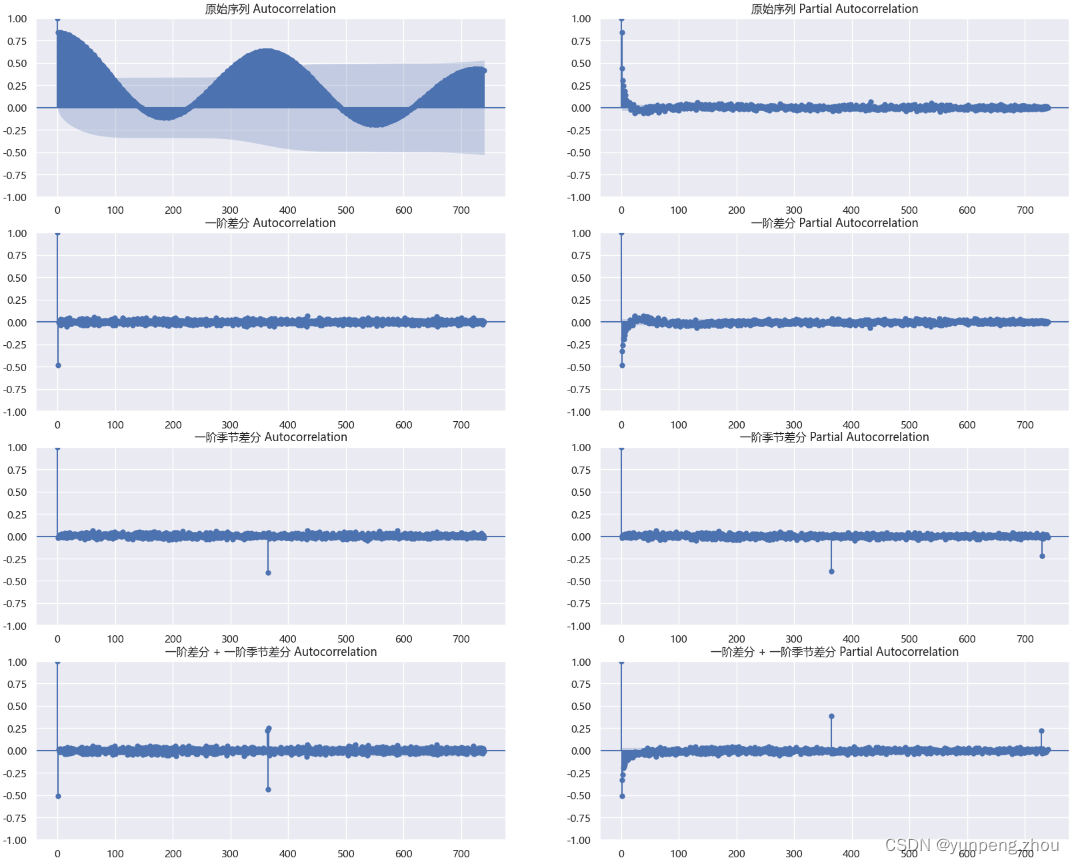
fg,axes = plt.subplots(4,2)for i,v in enumerate([('原始序列','number_sold'),('一阶差分','number_sold_diff'),('一阶季节差分','number_sold_season_diff'),('一阶差分 + 一阶季节差分','number_sold_diff_season')]):_ = plot_acf(data_train[v[1]],axes[i][0],lags=740) # 滞后选740 是因为从原始序列图上看,序列具有年(365)周期性, 740>2*T:查看跨两个周期的相关性_ = plot_pacf(data_train[v[1]],axes[i][1],lags=740)axes[i][0].set_title(f'{v[0]} Autocorrelation')axes[i][1].set_title(f'{v[0]} Partial Autocorrelation')fg.set_size_inches(20,16)
3.1.3 自相关 和 偏自相关 说明的问题
# 1. 测试序列(探究 acf 和 pacf 底层计算原理 )
test_y = np.array(data_train['number_sold_season_diff'])# 2. 自相关性:观测值序列 y_t 和 自身滞后K项 y-k 序列的皮尔逊相关系数,探究 y_t 和 y-k 的相关性
acf_values = sm.acf(test_y) # 使用statsmodels 库计算acf
acf_values # [ 1.00000000e+00, -2.15194759e-02, 1.94488838e-03, -9.45217080e-03,...]# 3. 偏相关性: 排除y_{t-1}、y_{t-2}...y{t-k+1}的影响后(排除原理看手动计算),观测值序列 y_t 和 自身滞后K项 y-k 序列的皮尔逊相关系数
pacf_values = sm.pacf(test_y)
pacf_values # [1.00000000e+00, -2.15268456e-02, 1.48350334e-03, -9.39249278e-03,...]# 4. 手动计算 acf 和 pacf(以k=2 为例)
y_t = test_y[2:] # y_t
y_t_1 = test_y[1:-1] # y_{t-1}
y_t_2 = test_y[:-2] # y_{t-2}# 自相关 直接求 x_t 和 x_{t-2}序列 的皮尔逊相关系数
acf_values_lag2 = np.corrcoef(y_t,y_t_2)[0,1] # np.corrcoef() 求两数组的协方差矩阵
acf_values_lag2 # 0.0019469889265725335 与 sm.acf 函数值 1.94488838e-03 基本一致# 求偏相关系数需要排除y_{t-1}的影响,分别对 y_t与y_{t_1} 和 y_{t-2}与y_{t_1}进行线性拟合,对拟合后的残差再计算相关性
p1 = np.polyfit(y_t_1,y_t_2,deg=1) # np.polyfit(x,y) 多项式拟合
residual_t_2 = np.polyval(p1,y_t_1) - y_t_2 # 计算拟合残差p2 = np.polyfit(y_t_1,y_t,deg=1)
residual_t = np.polyval(p2,y_t_1) - y_tpacf_values_lag2 = np.corrcoef(residual_t_2,residual_t)[0,1] # 计算残差间协方差矩阵
pacf_values_lag2 # 0.001487371254079463 与 sm.pacf 函数得出的值 1.48350334e-03 基本一致
**网传:**pacf 图截尾,acf 图拖尾 使用ar模型;pacf 图拖尾,acf 图截尾 使用ma模型;pacf 图和acf图同时拖尾或截尾 使用arma模型。(不是太理解)
个人理解:
自相关acf图:直接衡量的是当前观测值(y_t)与过去观测值(y_(t-k))之间的相关性,包括直接或间接的相关性(随机生成两组数,两者之间皮尔逊系数可能都不为0)。
偏自相关pacf图:y_t 除去y_(t-1)、y_(t-2) … y_(t-k+1) 已经解释部分后,y_(t-k)还单独可以贡献多少价值,更直接地说明了y_t 与 y_(t-k) 两者之间的相关性。
pacf 比 acf 好处: 如ar(2)模型,y_(t-1) 已经包含y_(t-2)几乎所有的信息,y_(t-2)可贡献剩余价值几乎没有的情况下,可以设为ar(1)模型 。减少滞后项、模型复杂度降低;可避免多重共线性问题。这可能是ar模型看pacf图截尾的原因。
3.1.4 ARIMA模型:
-
AR模型(AutoRegressive Model) 自回归模型:利用自身过去值的线性组合进行建模,预测当前值。
Y t = c + ψ 1 Y t − 1 + ψ 2 Y t − 2 + . . . + ψ p Y t − p + ε t p 阶自回归公式 其中: c 为常量, ψ 为自回归系数, Y t − p 为 t − p 时刻的观察值, ε t 误差项 Y_t = c+\psi_1Y_{t-1}+\psi_2Y_{t-2}+ ...+\psi_pY_{t-p}+\varepsilon_t \quad\quad p阶自回归公式\\ 其中:c为常量,\psi为自回归系数,Y_{t-p}为t-p时刻的观察值,\varepsilon_t 误差项 Yt=c+ψ1Yt−1+ψ2Yt−2+...+ψpYt−p+εtp阶自回归公式其中:c为常量,ψ为自回归系数,Yt−p为t−p时刻的观察值,εt误差项
前提假设:1. 时序依赖: 当前观测值与前p个时刻的观测值之间存在线性关系 2. 时序衰减: 当前观测值与近期过去的观测值相关强,与距今较远时刻的观测值相关性减弱或无相关。# 1. AR模型 model_ar = sm.AutoReg(endog=data_train['number_sold'], # 观测值lags=3, # 自回归阶数 这里试过1,3,7,10 效果几乎无差别trend='ct', # 包含常数项c和趋势项trendseasonal=True, # 开启季节性period=365, # 季节性周期exog = None # 引入外部变量) model_ar_res = model_ar.fit() res = model_ar_res.forecast(steps=data_test.shape[0])# 2. 绘制测试集拟合效果图 plt.figure(figsize=(20,5)) plt.plot(data_train['Date'],data_train['number_sold'],label='训练观测值') plt.plot(data_test['Date'],data_test['number_sold'],label='测试观测值') plt.plot(data_test['Date'],res,label='测试预估值') plt.title('ar自回归') plt.legend()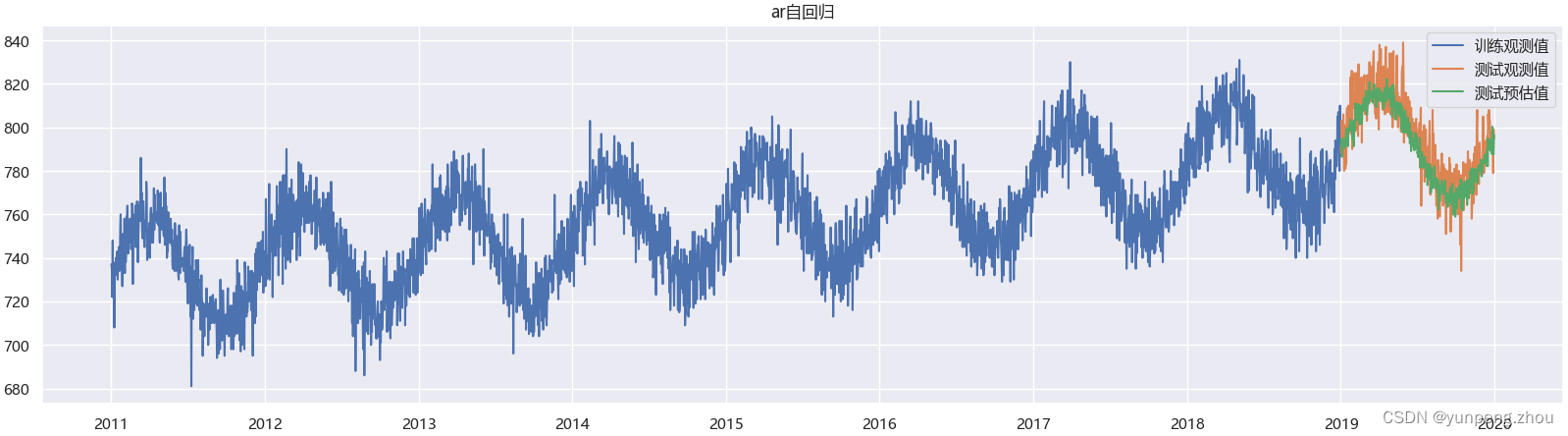
AutoReg 自回归模型 底层执行原理:
1. 根据参数创建特征变量X [ 常数项系数1(c),索引序号(trend), 365天哑变量(seasonal),L1、L2、L3 (p阶滞后项) ] 。2. 将特征X 与 y 观测值作岭回归拟合。3. 逐步迭代预估未来值(每一步预测值是下一步预测的滞后值)[具体流程可参考[LR复现ar]](#lr)# 1. AR 初始化生产X特征变量 exog = model_ar._x[0] # 第一个样本特征值 exog_names = model_ar.exog_names # 样本变量名称 np.hstack((np.array(exog_names).reshape(-1,1),np.array(exog).reshape(-1,1)))''' array([['const', '1.0'], # 第一项常数项,初始化为1['trend', '4.0'], # 趋势项索引,初始化为4,因为前3项属于滞后项 ['s(2,365)', '0.0'], # 365年季节性哑变量['s(3,365)', '0.0'],['s(4,365)', '1.0'],['s(5,365)', '0.0'],['s(6,365)', '0.0'],...['s(364,365)', '0.0'],['s(365,365)', '0.0'],['number_sold.L1', '722.0'], # 3阶滞后项['number_sold.L2', '735.0'],['number_sold.L3', '737.0'], ''' -
MA模型(Moving Average Model) 移动平均模型:利用自身过去项随机误差的线性组合进行建模,目的消除预测中随机扰动误差。
Y t = μ + ε t + θ 1 ε t − 1 + θ 2 ε t − 2 + . . . + θ q ε t − q q 阶移动平均 其中: μ 为序列均值或期望, θ 为回归系数, ε t 当前误差 , ε t − q 为 t − q 时刻误差或噪声 Y_t = \mu+\varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+ ...+\theta_q\varepsilon_{t-q} \quad\quad q阶移动平均\\ 其中:\mu为序列均值或期望,\theta为回归系数,\varepsilon_t 当前误差,\varepsilon_{t-q}为t-q时刻误差或噪声 Yt=μ+εt+θ1εt−1+θ2εt−2+...+θqεt−qq阶移动平均其中:μ为序列均值或期望,θ为回归系数,εt当前误差,εt−q为t−q时刻误差或噪声
前提假设:- 时间序列为平稳序列(具有常数的均值和方差)
- 时序依赖:当前观测值与过去时刻的误差项之间存在关联
- 时序衰减:当前观测值与近期过去的误差项相关强,与距今较远时刻的误差项相关性减弱或无相关。
*与AR模型区别:
AR: 认为当前值与过去p个时刻内观测值线性相关。
MR: 大部分时候时间序列应该是稳定的(即一段时间内,时间序列应该围绕着某个均值上下波动),在稳定的基础上,某个时刻的值受过去q个时刻的随机误差影响(说是随机误差,更像是过去因偶然事件产生的数值误差,会对未来造成隐形,如前q天因雨天影响突然降低的客户数,会在未来几天到来),MA能有效地消除预测中的偶然误差带来的波动。
# 1. MA 模型 # 创建ma测试数据ma(1) test_data_ma = pd.DataFrame({'c': [1 for i in range(120)],'noise':0}) # 均值为1 random_index = np.array(random.sample(set(test_data_ma.index[:-1]),k=30)+[99]) test_data_ma.loc[random_index,'noise'] = test_data_ma.loc[random_index,'noise'] - 2 # 假设 t-1 时刻因特殊原因顾客- 2,t时刻会回补 test_data_ma.loc[random_index+1,'noise'] = test_data_ma.loc[random_index+1,'noise'] + 2 test_data_ma['c + noise'] = test_data_ma['c'] + test_data_ma['noise']# 2. 分训练与测试 test_ma_train = test_data_ma.iloc[:100,:] test_ma_test = test_data_ma.iloc[100:,:]# 3. 拟合预测 model_ma = sm.ARIMA(endog=test_ma_train['c + noise'],order=(0,0,1)) model_ma = model_ma.fit() res = model_ma.forecast(steps=test_ma_test.shape[0])# 4. 绘制拟合效果图 plt.figure(figsize=(12,3)) plt.plot(test_ma_train.index,test_ma_train['c + noise'],label='训练观测值',linestyle=':',marker='.') plt.plot(test_ma_test.index,test_ma_test['c + noise'],label='测试观测值',linestyle=':',marker='.') plt.plot(test_ma_test.index,res,label='测试预估值',linewidth=3,c='r',linestyle='-.',marker='.') plt.legend() plt.title('ma 模型')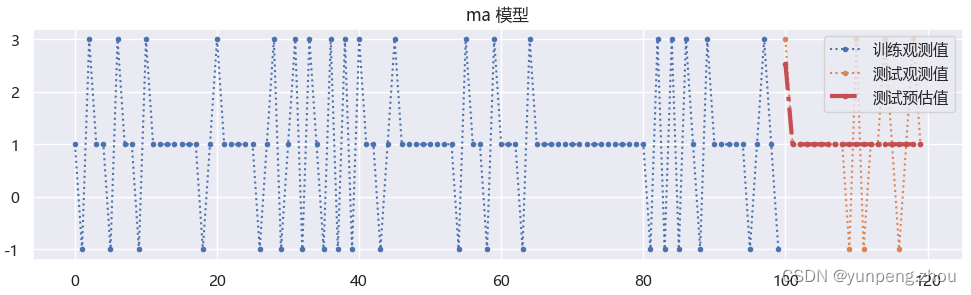
如图:在99时刻误差 -2 预测100时刻时,进行了回补。但>100时刻预估值全部为1(均值),是因为公式中
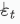 项预测时未来误差未知。
项预测时未来误差未知。**ma底层原理:**ma模型拟合的主要是误差。
-
初始误差 = 观测值 - 1 (在statsmodels中ma模型假定初次拟合值全部为1)
-
然后按误差进行自回归线性拟合,求新拟合值 。
-
将新拟合值与观测值相减求新误差。
-
重复 2、3步 直到达到最大迭代次数或新误差小于设定值。
-
**ARIMA模型 ** : 将AR模型与MA 进行组合(查看底层math如下)
KaTeX parse error: Expected 'EOF', got '&' at position 65: …{k}-X_{t}\beta=&̲\epsilon_{t} \\…上述公式确实没看懂 (符号数学)以下纯个人理解
- 滞后算子
L : 滞后算子,代表着一种滞后操作, L y t = y t − 1 、 L 2 y t = y t − 2 . . . L k y t = y t − k ( 1 − L ) y t : 表示对 y t 序列做一阶差分, ( 1 − L ) d y t : 表示对 y t 序列做 d 阶差分 L: 滞后算子,代表着一种滞后操作,Ly_t=y_{t-1}、L^2y_t=y_{t-2} ... L^ky_t=y_{t-k}\\ (1-L)y_t:表示对y_t序列做一阶差分,(1-L)^dy_t:表示对y_t序列做d阶差分\\ L:滞后算子,代表着一种滞后操作,Lyt=yt−1、L2yt=yt−2...Lkyt=yt−k(1−L)yt:表示对yt序列做一阶差分,(1−L)dyt:表示对yt序列做d阶差分
-
ar部分
y t = ψ 1 y t − 1 + ψ 2 y t − 2 + . . . + ψ p y t − p + ε t y t = ψ 1 L y t + ψ 2 L 2 y t + . . . + ψ p L P y t + ε t ε t = ( 1 − c + ψ 1 L + ψ 2 L 2 + . . . + ψ p L P ) y t ε t = Φ ( L ) y t y_t = \psi_1y_{t-1}+\psi_2y_{t-2}+ ...+\psi_py_{t-p}+\varepsilon_t\\ y_t = \psi_1Ly_t+\psi_2L^2y_t+ ...+\psi_pL^Py_t+\varepsilon_t\\ \varepsilon_t = (1 - c+\psi_1L+\psi_2L^2+ ...+\psi_pL^P)y_t\\ \varepsilon_t =\Phi(L)y_t yt=ψ1yt−1+ψ2yt−2+...+ψpyt−p+εtyt=ψ1Lyt+ψ2L2yt+...+ψpLPyt+εtεt=(1−c+ψ1L+ψ2L2+...+ψpLP)ytεt=Φ(L)yt -
ma部分
y t = ε t + θ 1 ε t − 1 + θ 2 ε t − 2 + . . . + θ q ε t − q y t = ε t + θ 1 L ε t + θ 2 L 2 ε t + . . . + θ q L q ε t y t = ( 1 + θ 1 L + θ 2 L 2 + θ q L q ) ε t y t = Θ ( L ) ε t y_t = \varepsilon_t+\theta_1\varepsilon_{t-1}+\theta_2\varepsilon_{t-2}+ ...+\theta_q\varepsilon_{t-q}\\ y_t = \varepsilon_t+\theta_1L\varepsilon_t+\theta_2L^2\varepsilon_t+ ...+\theta_qL^q\varepsilon_t\\ y_t = (1+\theta_1L+\theta_2L^2+\theta_qL^q)\varepsilon_t\\ y_t = \Theta(L)\varepsilon_t yt=εt+θ1εt−1+θ2εt−2+...+θqεt−qyt=εt+θ1Lεt+θ2L2εt+...+θqLqεtyt=(1+θ1L+θ2L2+θqLq)εtyt=Θ(L)εt -
arima(若ar与ma结合,ma模型拟合的目标
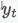 是ar拟合后的误差部分
是ar拟合后的误差部分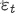 )
)
m a 公式变换形式: ε t = μ + Θ ( L ) η t 则 a r m a : Φ ( L ) y t = Θ ( L ) ε t 对 y t 进行差分: Φ ( L ) ( 1 − L ) d y t = Θ ( L ) ε t ma公式变换形式:\\ \varepsilon_t = \mu+\Theta(L)\eta_{t}\\ 则arma:\\ \Phi(L)y_t=\Theta(L)\varepsilon_t\\ 对y_t进行差分:\\ \Phi(L)(1-L)^dy_t=\Theta(L)\varepsilon_t ma公式变换形式:εt=μ+Θ(L)ηt则arma:Φ(L)yt=Θ(L)εt对yt进行差分:Φ(L)(1−L)dyt=Θ(L)εt
# 1. arima 模型 model_arima = sm.ARIMA(endog=data_train['number_sold'],order=(3,0,1),seasonal_order=(1,1,0,365),trend='t') model_arima = model_arima.fit(method='innovations_mle', low_memory=True, cov_type='none') # period=365 周期太长 ,拟合跑的很慢,大概耗时 10min res = model_arima.forecast(steps=data_test.shape[0])# 2. 绘制arima预测效果 plt.figure(figsize=(20,5)) plt.plot(data_train['Date'],data_train['number_sold'],label='训练观测值') plt.plot(data_test['Date'],data_test['number_sold'],label='测试观测值') plt.plot(data_test['Date'],res,label='测试预估值') plt.title('arima 季节移动平均自回归') plt.legend()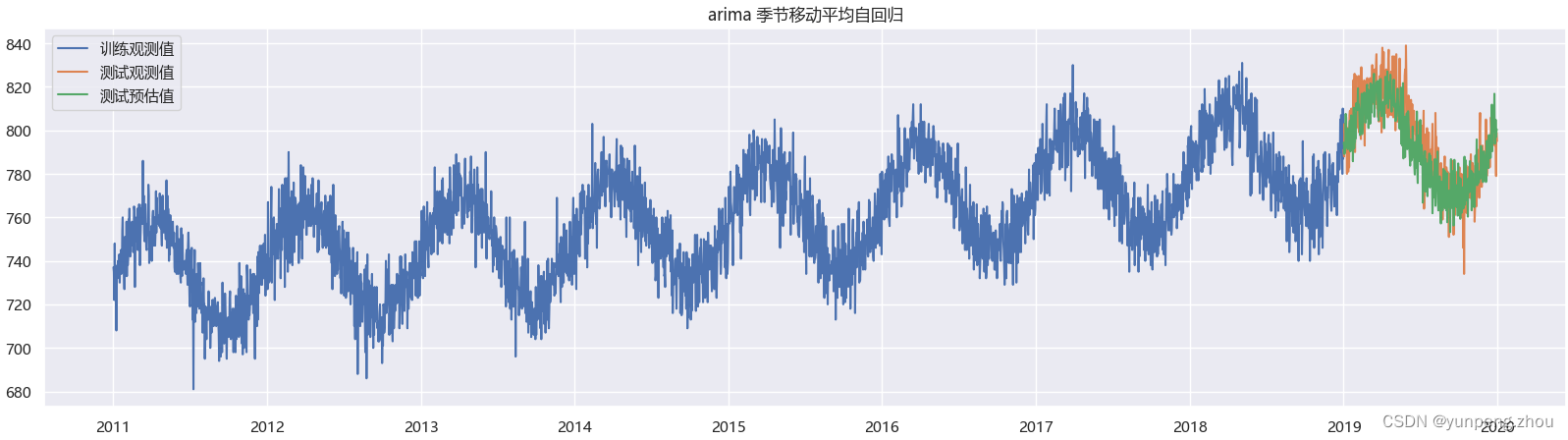
如图:在AR模型的基础上加上ma模型误差弥补,预估效果改善不少。
3.2 机器学习模型
3.2.1 LR (线性回归)
# 1.lr 模型 按照AutoReg自回归模型创建X特征矩阵
# 参数
maxlag = 3 # 滞后阶级
s = 365 # 季节性周期# 2. 创建二维滞后数组函数
def lagmat(x,maxlag):x_ = np.zeros((x.shape[0],maxlag))for i in range(maxlag):x_[:,i] = x.shift(-i)return np.roll(x_,shift=maxlag,axis=0)# 3. 生产训练集X特征
data_lr_train = pd.DataFrame({'date':data_train['Date'],'y':data_train['number_sold'],'trend':np.arange(data_train.shape[0])})
data_lr_train['seasonal'] = data_lr_train['date'].dt.dayofyear# 4. 数据编码(季节性编码)
onehotencoder = OneHotEncoder()
data_lr_train.loc[:,[f's.{i}'for i in range(s+1)]] = onehotencoder.fit_transform(data_lr_train.loc[:,['seasonal']]).toarray()# 5. 添加滞后列
data_lr_train.loc[:,[f'L{i}' for i in range(1,maxlag+1)]] = lagmat(data_train['number_sold'],maxlag)
data_lr_train = data_lr_train.iloc[maxlag+1:,:] # 剔除初始无滞后项数据# data_lr_train
# date y trend seasonal s.0 s.1 s.2 s.3 s.4 s.5 ... s.359 s.360 s.361 s.362 s.363 s.364 s.365 L1 L2 L3
# 2011-01-06 727 4 6 0.0 0.0 0.0 0.0 0.0 1.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 735.0 722.0 748.0
# 2011-01-07 735 5 7 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 722.0 748.0 727.0
# 2011-01-08 733 6 8 0.0 0.0 0.0 0.0 0.0 0.0 ... 0.0 0.0 0.0 0.0 0.0 0.0 0.0 748.0 727.0 735.0# 6.生成测试集
data_lr_test = pd.DataFrame({'date':data_test['Date'],'y':data_test['number_sold'],'trend':np.arange(data_train.shape[0],data_train.shape[0]+data_test.shape[0])})
data_lr_test['seasonal'] = data_lr_test['date'].dt.dayofyear
data_lr_test.loc[:,[f's.{i}'for i in range(s+1)]] = onehotencoder.transform(data_lr_test.loc[:,['seasonal']]).toarray()train_x,train_y = data_lr_train.iloc[:,2:],data_lr_train['y']# 7. 岭回归
lr = Ridge()
lr.fit(train_x,train_y)# 8. lr逐步迭代预测函数(将上一步预测结果放本次预测的滞后项特征上,迭代预测)
def forecast(estimator,data_test=data_lr_test):pre_lag = data_lr_train['y'][-maxlag:] # 测试集初始滞后项(取训练集后p项)res = [] # 存储逐步预测结果for i in range(data_lr_test.shape[0]):test_x = np.r_[data_lr_test.iloc[i,2:],pre_lag].reshape(1,-1) new_y = estimator.predict(test_x)pre_lag = np.r_[pre_lag,new_y][-maxlag:]res.append(new_y[0])return resres = forecast(lr,data_lr_test)# 9. 结果可视化
plt.figure(figsize=(20,5))
plt.plot(data_train['Date'],data_train['number_sold'],label='训练观测值')
plt.plot(data_test['Date'],data_test['number_sold'],label='测试观测值')
plt.plot(data_test['Date'],res,label='测试预估值')
plt.title('按照ar自回归模型参数执行岭回归')
plt.legend()
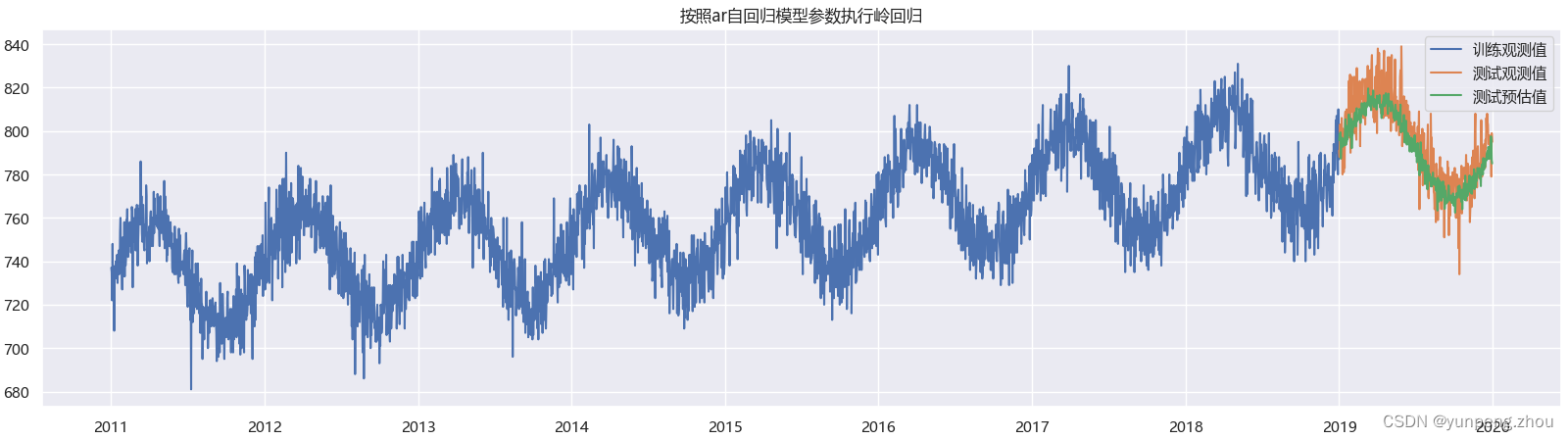
如图:lr模型复现效果几乎与statsmodel中ar自回归预测结果一致。
3.2.2 Xgboost
# 1. xgboost 使用特征与lr保持一致
params = { 'eta': 0.3,'gamma': 0,'max_depth': 6,'lambda':1, # L2正则'objective':'reg:squarederror','eval_metric':'mae'}dtrain = xgb.DMatrix(data=train_x,label=train_y)
xgb_model = xgb.train(params=params,dtrain=dtrain,num_boost_round=20)# 2. 逐步迭代预测函数(将上一步预测结果放本次预测的滞后项特征上,迭代预测)
def forecast(estimator,data_test=data_test):pre_lag = data_lr_train['y'][-maxlag:] # 测试集初始滞后项(取训练集后p项)res = [] # 存储逐步预测结果for i in range(data_lr_test.shape[0]):test_x = np.r_[data_lr_test.iloc[i,2:],pre_lag].reshape(1,-1) new_y = estimator.predict(xgb.DMatrix(test_x,feature_names=list(data_lr_test.columns[2:])+[f'L{i}' for i in range(1,pre_lag.shape[0]+1)]))pre_lag = np.r_[pre_lag,new_y][-maxlag:]res.append(new_y[0])return resres = forecast(xgb_model,data_test)# 3. 结果可视化
fg = plt.figure(figsize=(20,5))
plt.plot(data_train['Date'],data_train['number_sold'],label='训练观测值')
plt.plot(data_test['Date'],data_test['number_sold'],label='测试观测值')
plt.plot(data_test['Date'],res,label='xgbt预估值')
plt.plot(data_test['Date'],[max(res) for i in res],label='预估最大值')
plt.title('按照ar自回归模型参数执行xgbt回归')
plt.legend()
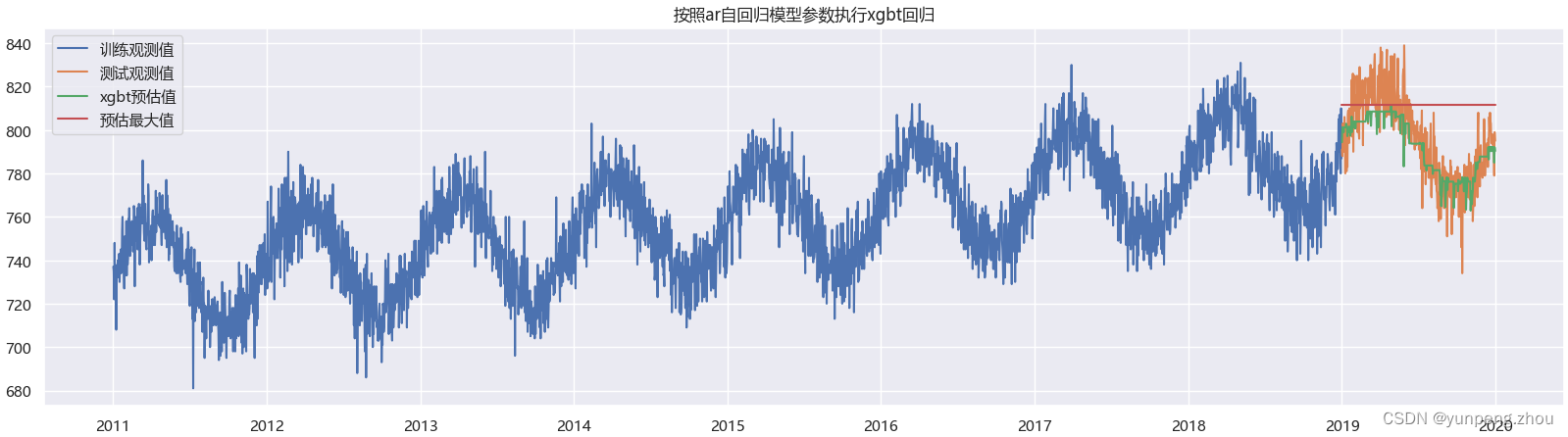
如图:xgbt 效果没有lr模型好,无法拟合趋势增加项(纯个人理解:lr 模型有带系数的trend项,能随着日期的增加逐渐变大,但xgbt树模型的分数,是对叶子节点上样本求均值,而训练集以时间前后切分,其中没有未来越来越大的观测值,模型就无法拟合更大值)
参考1: https://baijiahao.baidu.com/s?id=1708325528423248703&wfr=spider&for=pc
参考2: https://www.xjx100.cn/news/555912.html?action=onClick