LeetCode T392 判断子序列
题目链接:392. 判断子序列 - 力扣(LeetCode)
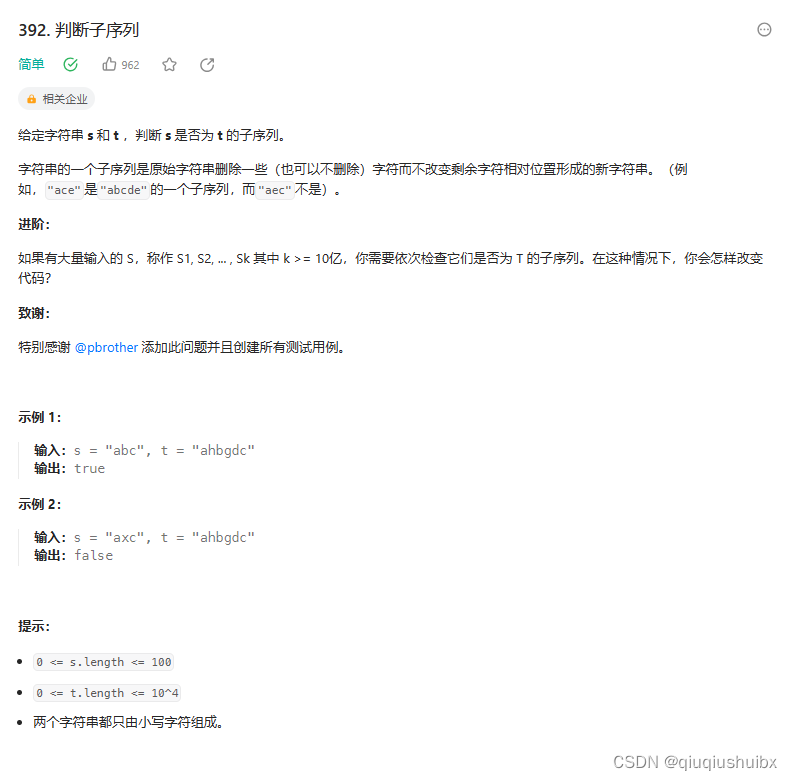
题目思路:
本题有两种思路,第一个思路是使用双指针,第二个思路是使用动态规划,结尾笔者会附上两种方法的代码.
1.双指针
首先我们谈双指针的思路,就是让两个指针分别指向s和t字符串的开头,只要遇到相同字母,两者同时向后走一步,如果没有遇到字符相同,则只有t指针向后走,最后只要判断走完不管是s或者是t先走完,只要判断s对应的指针下标大小是否和其长度一样即可
2.动态规划(和最长公共子序列基本一样)
2.1 明确dp数组含义
dp数组表示的是结尾为i-1和结尾为j-1的s和t字符串匹配的字符数量
2.2 明确dp数组递推公式
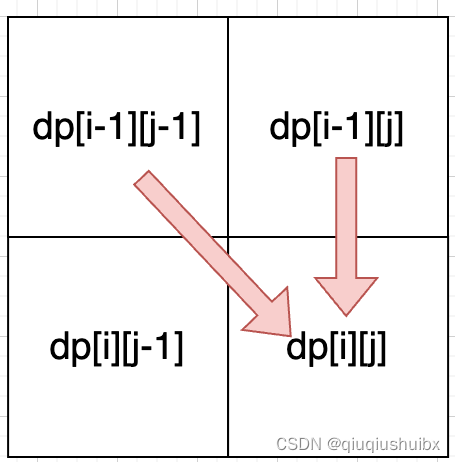
如果遇到相等就是dp[i][j] = dp[i-1][j-1] + 1
不相等就是 dp[i][j] = dp[i-1][j]
2.3 初始化dp数组
无需初始化
2.4 明确遍历顺序
顺序遍历即可
2.5 打印dp数组排错
题目代码:
//动态规划
class Solution {public boolean isSubsequence(String s, String t) {int len1 = s.length();int len2 = t.length();int[][] dp = new int[len1+1][len2+1];for(int i = 1;i<=len1;i++){char c1 = s.charAt(i-1);for(int j = 1;j<=len2;j++){char c2 = t.charAt(j-1);if(c1 == c2){dp[i][j] = dp[i-1][j-1]+1;}else{dp[i][j] = Math.max(dp[i-1][j],dp[i][j-1]);}}}if(dp[len1][len2] == len1){return true;}else{return false;}}
}//双指针class Solution {public boolean isSubsequence(String s, String t) {int len1 = s.length();int len2 = t.length();int i = 0,j = 0;while(i<len1 && j<len2){if(s.charAt(i) == t.charAt(j)){i++;j++;}else{j++;}}return i == len1;}
}LeetCode T115 不同的子序列
题目链接:115. 不同的子序列 - 力扣(LeetCode)

题目思路:
1确定dp数组含义
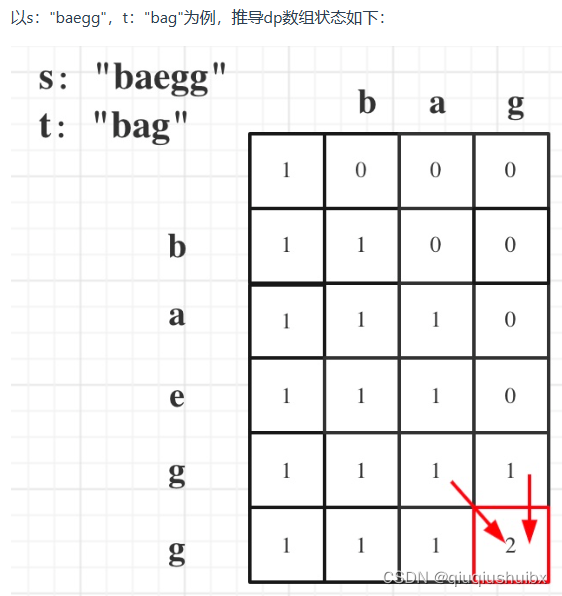
这里的dp[i][j]表示以i-1为结尾的s子序列中出现以j-1为结尾的t的个数为dp[i][j]。
2.确定递推公式
- s[i - 1] 与 t[j - 1]相等
- s[i - 1] 与 t[j - 1] 不相等
当s[i - 1] 与 t[j - 1]相等时,dp[i][j]可以有两部分组成。
一部分是用s[i - 1]来匹配,那么个数为dp[i - 1][j - 1]。即不需要考虑当前s子串和t子串的最后一位字母,所以只需要 dp[i-1][j-1]。
一部分是不用s[i - 1]来匹配,个数为dp[i - 1][j]。
举例,假设s = 'rara',t = 'ra'
这时候我们用最后一个a,那么其实s的最后一个a消掉,t的最后一个a也消掉,那么其实就是 dp[i-1][j-1]
这个时候如果不用最后一个字母a,就是在前面''rar''看有没有''ra'',就是dp[i-1][j]
当最后一个字母不同的时候,其实也不用考虑了,比如'rarb'这里b也用不上呀,只能向前看 dp[i-1][j]是否有满足条件的结果
3.初始化dp数组
dp[i][0] 表示:以i-1为结尾的s可以随便删除元素,出现空字符串的个数。
那么dp[i][0]一定都是1,因为也就是把以i-1为结尾的s,删除所有元素,出现空字符串的个数就是1。
4.确定遍历方式
从前向后遍历,因为后者依赖前者产生
5.打印数组排错
题目代码:
class Solution {public int numDistinct(String s, String t) {int len1 = s.length();int len2 = t.length();int[][] dp = new int[len1+1][len2+1];for(int i = 0;i<len1+1;i++){dp[i][0] = 1;}for(int i = 1;i<=len1;i++){char c1 = s.charAt(i-1);for(int j = 1;j<=len2;j++){char c2 = t.charAt(j-1);if(c1 == c2){dp[i][j] = dp[i-1][j-1] + dp[i-1][j];}else{dp[i][j] = dp[i-1][j];}}}return dp[len1][len2];}
}