数学建模学习之发动机最优生产计划模型求解-编程知识

数学建模学习之发动机最优生产计划模型求解

问题重述

某工厂向用户提供发动机，按合同规定，其交货数量和日期是:第一季末交 40 台第二季末交 60 台，第三季末交 80 台。工厂的最大生产能力为每季 100 台，每季的生产费用是 $50x+0.2x^{2}$ (元)，此处为该季生产发动机的台数。若工厂生产得多，多余的发动机可移到下一季度向用户交货，此时工厂就需支付存储费，每台发动机每季的存储费为 4 元。问该厂每季应生产多少台发动机，才能既满足交货合同，又使工厂所花费的费用最少(假定第一季度无存货)?

分析：根据问题，三个季度，每一个季度生产费用 $50x+0.2x^{2}$ ，另外还有存储费用，要求最小费用即求出生产费用与存储费用最小。

生产费用：

$L(\theta )=50x_{i}+0.2x_{i}^{2}(i=1,2,3)$

存储费用：

$S(\theta )=4(x_{1}-40)+4(x_{1}-40+x_{2}-60)=4(2x_{1}+x_{2}-140)$

由题中可知：约束条件为

$\begin{cases} x_{1}\geqslant 40 & \text{ } \\ x_{1}+x_{2} \geqslant 100& \text{ } \\ x_{1}+x_{2}+x_{3}= 180& \text{ } \end{cases}$

接下来就可以建立数学模型了

$minf(x)=\sum_{i=1}^{3}(50x_{i}+0.2x_{i}^{2})+4(x_{1}-40)+4(x_{1}+x_{2}-100)$

$s.t.\begin{cases} x_{1} \geqslant 40& \text{ } \\ x_{1}+x_{2}\geqslant 100& \text{ } \\ x_{1}+x_{2} x_{3}=180& \text{ } \\ x_{1}\leqslant 100,x_{2}\leqslant 100,x_{3}\leqslant 100& \text{ } \end{cases}$

其中 $x_{1},x_{2},x_{3}$ 为正整数。

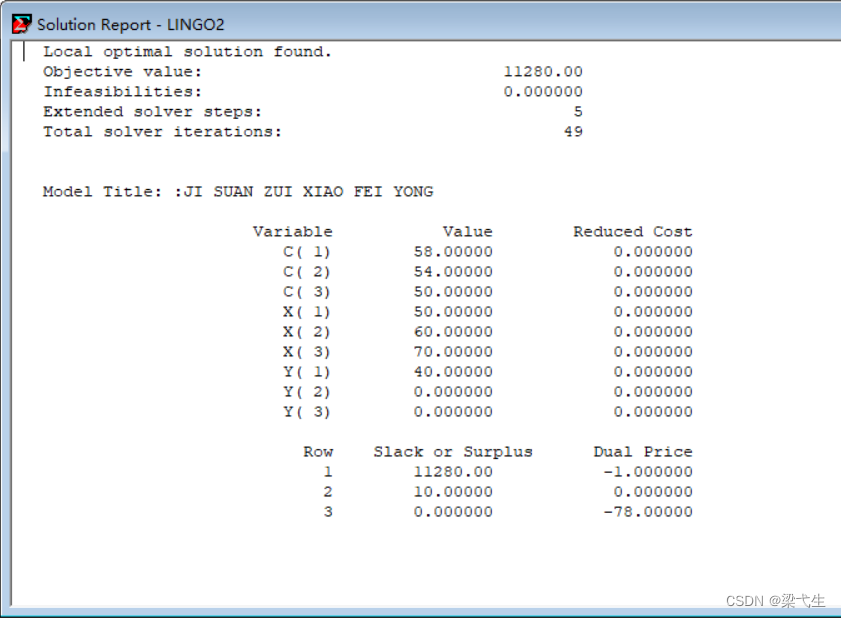
model:
title:JI SUAN ZUI XIAO FEI YONG;
sets:
jidu/1..3/:c,x,y;
endsets
data:
c = 58 54 50;!函数的一次项系数;
y = 40 0 0;!下界向量即第一个季度最低要生产四十个;
enddata
min=0.2*@sum(jidu:x^2)+@sum(jidu:c*x)-560;
x(1)+x(2)>100;
@sum(jidu:x)=180;
@for(jidu:@bnd(y,x,100));
end

第二种代码

Model:	
Title this is a optimal production program;	
min=0.2*(x1^2+x2^2+x3^2)+58*x1+54*x2+50*x3-560;	
x1>=40;
x1+x2>=100;	
x1+x2+x3=180;	
x1<=100;	
x2<=100;	
x3<=100;	
@gin(x1);@gin(x2);@gin(x3);	
end

这俩代码解出来的结果是一样的