文章目录
- 记忆化搜索
- 斐波那契数列
- 例题
- 不同路径
- 最长递增子序列
- 猜数字大小
- 矩阵中的最长递增路径
记忆化搜索的原理其实很简单,简单来说就是对暴力搜索的一些优化,因此整体上来讲难度不高
记忆化搜索
所谓记忆化搜索,直白来说就是一个带有备忘录的递归
如何实现记忆化搜索?
- 添加一个备忘录
- 递归每次返回的时候,都把结果放在备忘录当中
- 每次进行递归前,都到备忘录中看一看
下面用一个经典题目诠释记忆化搜索的意义
斐波那契数列

- 递归
class Solution
{
public:// 递归int fib(int n) {if(n == 0 || n == 1) return n;return fib(n - 1) + fib(n - 2);}
};
- 动态规划
class Solution
{
public:// 动态规划int fib(int n) {if(n == 0 || n == 1)return n;vector<int> v(n + 1);v[0] = 0, v[1] = 1;for(int i = 2; i <= n; i++)v[i] = v[i - 1] + v[i - 2];return v[n];}
};
- 记忆化搜索
class Solution
{
public:// 记忆化搜索int memo[31];int fib(int n) {// 先到备忘录中看看if(memo[n] != 0)return memo[n];if(n == 0 || n == 1){memo[n] = n;return memo[n];}return fib(n - 1) + fib(n - 2);}
};
从上面这个例题能感觉出来,记忆化搜索其实就是在递归的基础上进行了一些优化,没有什么本质性的新增内容,基于这个原因,用下面的例题来进一步学习记忆化搜索
例题
不同路径

暴力搜索
class Solution
{
public:int dfs(int m, int n, int p, int q){if(m > p || n > q) return 0;if(m == p && n == q) return 1;return dfs(m + 1, n, p, q) + dfs(m, n + 1, p, q);}int uniquePaths(int m, int n) {return dfs(0, 0, m - 1, n - 1);}
};
采用记忆化搜索进行一定程度的优化
class Solution
{
public:int arr[101][101];int dfs(int m, int n, int p, int q){if(arr[m][n] != 0) return arr[m][n];if(m > p || n > q) return 0;if(m == p && n == q) return 1;int down = dfs(m + 1, n, p, q);int right = dfs(m, n + 1, p, q);arr[m + 1][n] = down;arr[m][n + 1] = right;return down + right;}int uniquePaths(int m, int n) {return dfs(0, 0, m - 1, n - 1);}
};
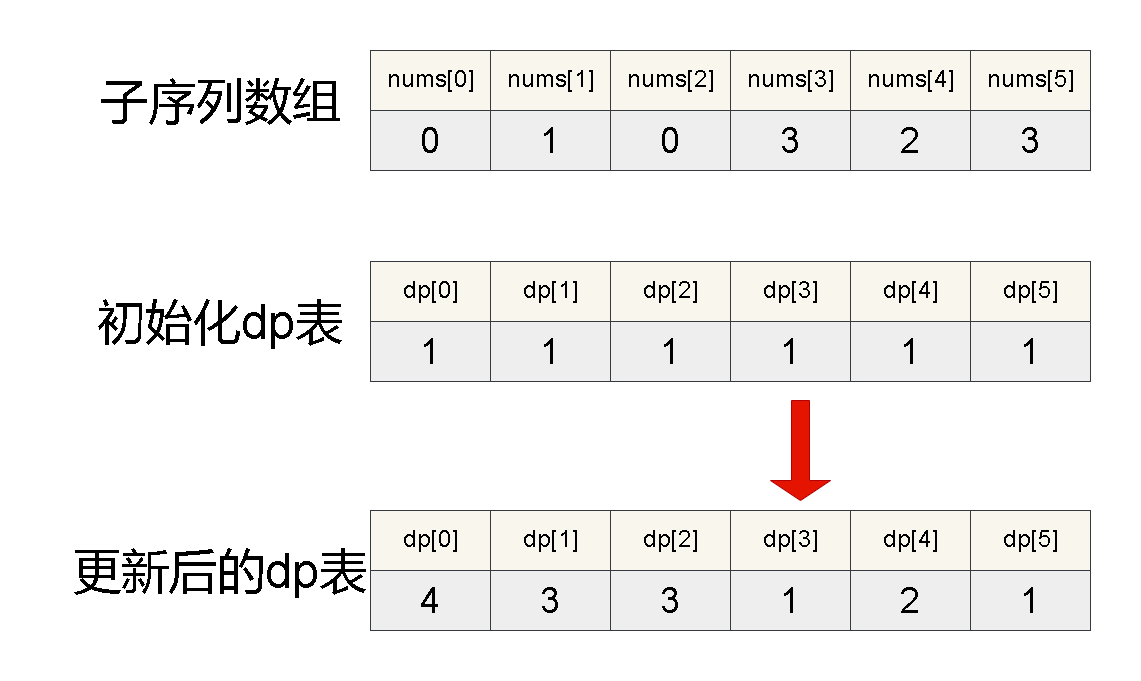
最长递增子序列

暴力搜索
class Solution
{
public:vector<int> path;int maxSize;int lengthOfLIS(vector<int>& nums){dfs(0, nums, INT_MIN);return maxSize;}void dfs(int pos, vector<int>& nums, int prev){maxSize = max(maxSize, (int)path.size());for (int i = pos; i < nums.size(); i++){if (nums[i] > prev){path.push_back(nums[i]);dfs(i + 1, nums, nums[i]);path.pop_back();}}}
};
记忆化搜索
class Solution
{
public:int memo[2501];int lengthOfLIS(vector<int>& nums) {int ret = 0;for(int i = 0; i < nums.size(); i++){ret = max(ret, dfs(i, nums));}return ret;}int dfs(int pos, vector<int>& nums){if(memo[pos] != 0) return memo[pos];int ret = 1;for(int i = pos + 1; i < nums.size(); i++){if(nums[i] > nums[pos]){ret = max(ret, dfs(i, nums) + 1);}}memo[pos] = ret;return ret;}
};
猜数字大小

暴力搜索
class Solution
{
public:int getMoneyAmount(int n) {return dfs(1, n);}int dfs(int begin, int end){if(begin >= end) return 0;int res = INT_MAX;// 选一个节点作为根节点for(int i = begin; i <= end; i++){// 找左子树花费的钱int left = i + dfs(begin, i - 1);// 找右子树花费的钱int right = i + dfs(i + 1, end);res = min(res, max(left, right));}return res;}
};
记忆化搜索优化
class Solution
{
public:vector<vector<int>> memo;int getMoneyAmount(int n) {memo.resize(n + 1, vector<int>(n + 1));return dfs(1, n);}int dfs(int begin, int end){if(begin >= end) return 0;if(memo[begin][end] != 0) return memo[begin][end];int res = INT_MAX;// 选一个节点作为根节点for(int i = begin; i <= end; i++){// 找左子树花费的钱int left = i + dfs(begin, i - 1);// 找右子树花费的钱int right = i + dfs(i + 1, end);res = min(res, max(left, right));}memo[begin][end] = res;return res;}
};
矩阵中的最长递增路径

记忆化搜索
class Solution
{
public:int m, n;int dx[4] = {0, 0, 1, -1};int dy[4] = {1, -1, 0, 0};vector<vector<int>> memo;int longestIncreasingPath(vector<vector<int>>& matrix) {m = matrix.size();n = matrix[0].size();memo.resize(m, vector<int>(n));int res = 0;for(int i = 0; i < m; i++){for(int j = 0; j < n; j++){res = max(res, dfs(i, j, matrix));}}return res;}// 从第i行和第j列的这个元素开始的最长递增路径int dfs(int i, int j, vector<vector<int>>& matrix){if(memo[i][j] != 0) return memo[i][j];int ret = 1;// 长度等于其四周的元素的最长递增路径for(int k = 0; k < 4; k++){int x = i + dx[k], y = j + dy[k];// 如果坐标合法并且是递增if(x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j]){ret = max(ret, 1 + dfs(x, y, matrix));}}memo[i][j] = ret;return ret;}
};