5.算法策略5：Graham Scan Algorithm
算法思路：
给定二维点集，求其凸包
1）presorting：
（1）先找到 ltl点 ，也就是y值最小的点，若是存在y值相等的点，再取x值最小的点。将该点压入到栈S中。
（2）再从 ltl点 出发，找到第二个特别的点，压入到S栈中。这个特别的点（暂时记作A）的特别之处在于点集中其他所有的点都在A和ltl的左侧（也就是 ToLeftTest(ltl,A,S) 为true）。
---------这时S栈中有两个元素
（3）将点集中剩余的其他点按照与 ltl-A 所成的角度排序，角度越大的，越早被压入T栈。这个找所成角度最大的那个点，把它压入栈中也比较动了动我的脑子。
---------这时T栈中按顺序放有点集中的其他元素
2）graham scan的核心算法
每次取S栈的次栈顶、栈顶 以及 T栈的栈顶 做 ToLeftTest。如果是true，代表T栈的栈顶元素要加入到S栈中来，否则当前S栈的栈顶元素将要被弹出，直到T栈变空为止。每次S栈的状态，都是当前scan到的凸包状态，然后也会有回退（backtrack）过程进行调整。
核心算法：
while(!T.empty())
if(toLeftTest(S[S.top-1],S[S.top],T[T.top]){
S.push(T.pop());
}
else{
S.pop();
}
理解起来还是可以的。
这里，邓俊辉老师的课程上没有提供presorting相关实现思路的代码（只是口头描述了一下），对我这种菜鸡造成了一定的困难。脑袋累累也许才能有所突破和进步，总是要有这么一个过程。数据结构也学过去好久了，但好在网上有构建栈、压入栈等的代码可以学习（不难）。总之，几番探索，搞定了S栈和T栈。真正的graham scan部分在实现上就那么几行代码（算法复杂度低）。
------------------------------------------------------------------------------------------------
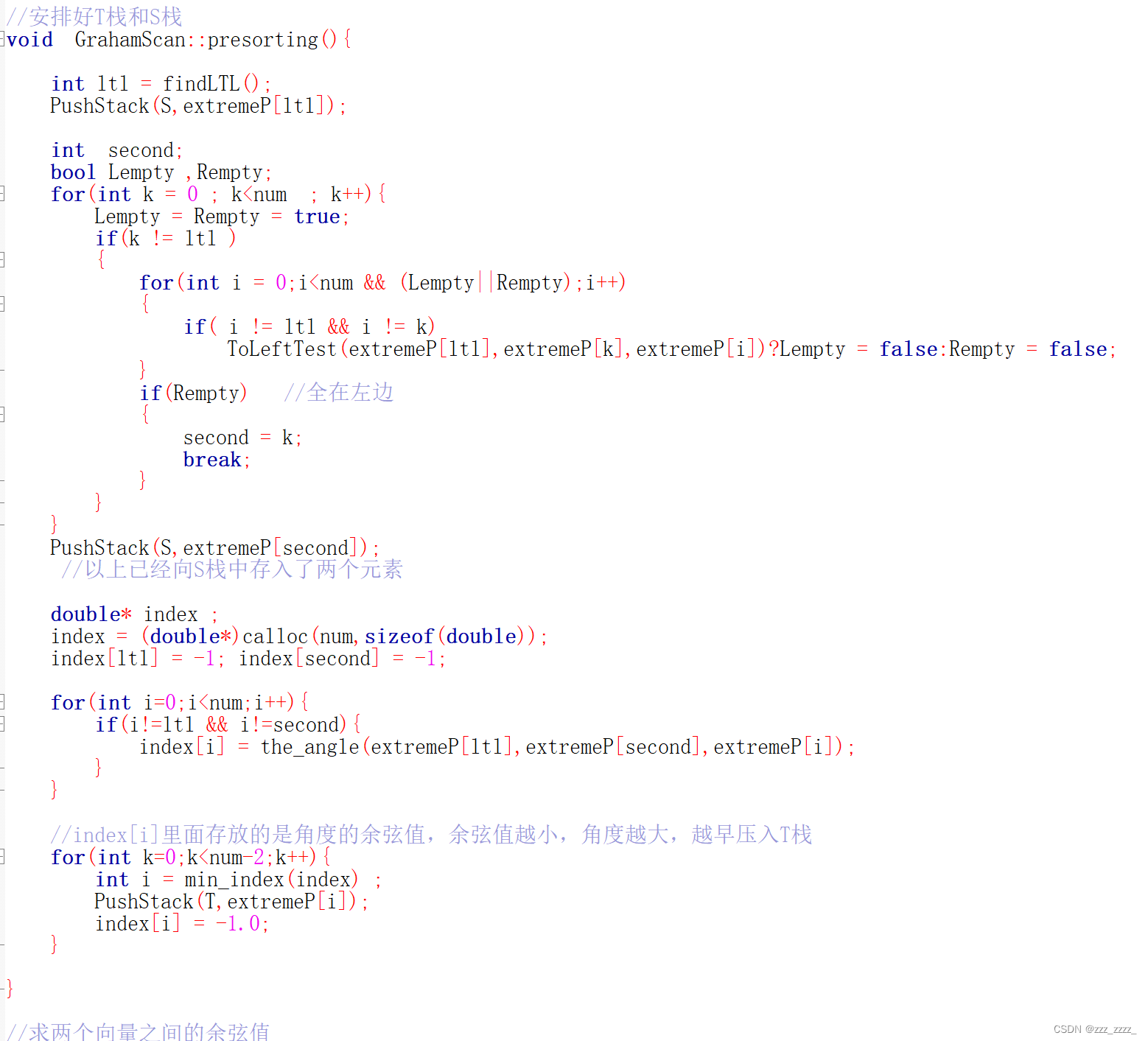
这里将已经压入栈中的元素对应的 index[i] 值标记为-1，index[i]值存入的是角度的cos值（除了压入栈中的元素对应存入的是-1），cos值的范围在-1-1之间的。
这些都是写在类中的，在主函数中构建对象，然后用opencv将极边画出来看看。极点都在最终的S栈中。
结果如下：
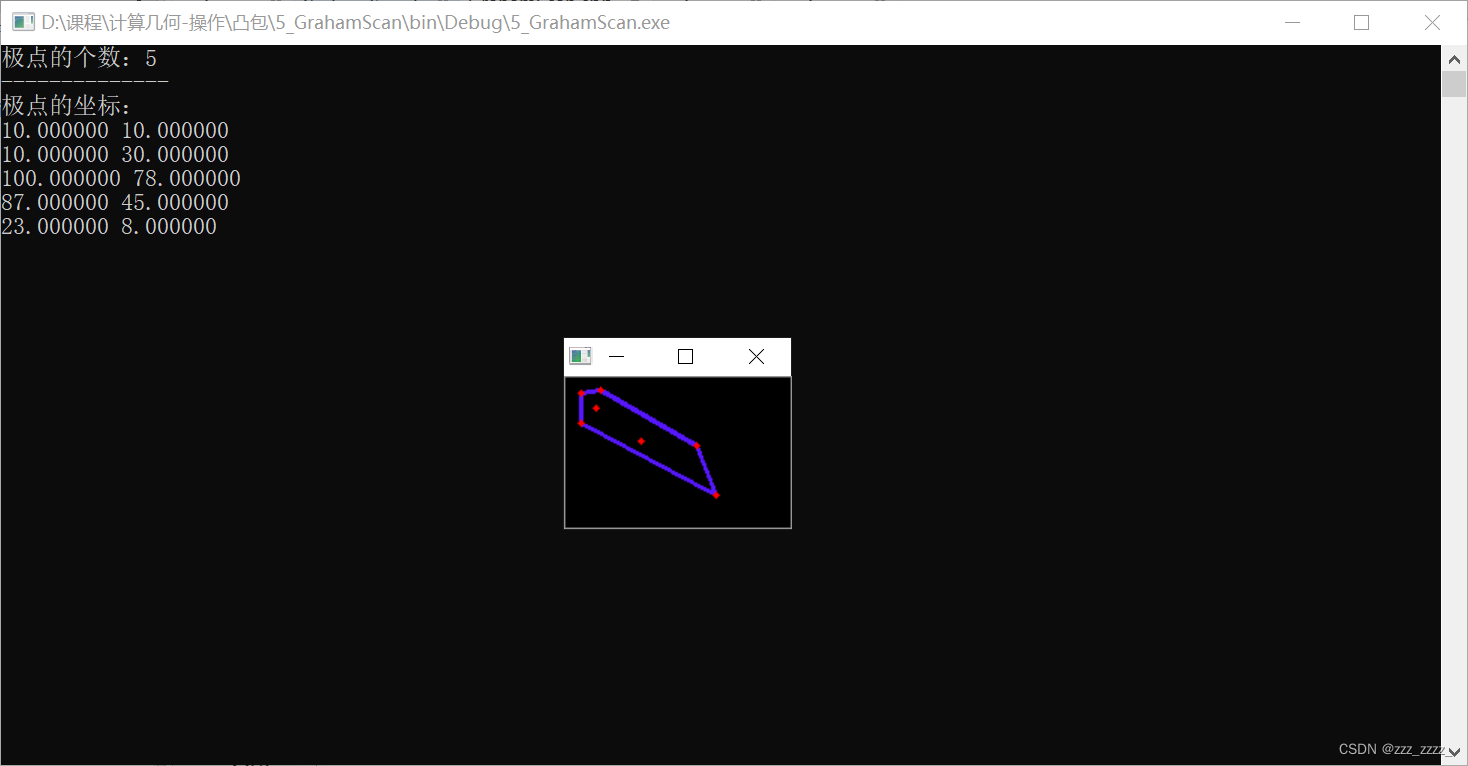
（念叨念叨）不知道cv领域的未来，多学是没有坏处的，但方向不对也不行。每天像过流水账一样，我的青春小鸟一样不回来。
