一、数据结构定义
typedef int VertexType;
typedef int EdgeType;/*图*/
typedef struct {VertexType Vexs[SIZE]; //结点 EdgeType Edges[SIZE][SIZE]; //权值 int vexnum, arcnum;
}MGraph;/*路径*/
typedef struct {int path[SIZE][SIZE];EdgeType length;
}Path;1.二维数组 Edges[SIZE][SIZE] 储存图的边权数据,一维数组 Vexs[SIZE] 储存图的结点数据;
2.结构体 Path 保存计算后的路径信息。
二、算法详解
/* 初始化图并输入权值 */
MGraph* InitGraph() {MGraph* G = (MGraph*)malloc(sizeof(MGraph));G->vexnum = 4;G->arcnum = 8;//初始化图的邻接矩阵 Edges[SIZE][SIZE]for (int i = 0; i < G->vexnum; i++) {for (int j = 0; j < G->vexnum; j++) {if (i == j) G->Edges[i][j] = 0; //对角线权值为0 else G->Edges[i][j] = MaxNum; //除对角线外所有权值为无穷大 }}//初始化图的结点矩阵 Vexs[SIZE]VertexType v[4] = { 0,1,2,3 };for (int i = 0; i < G->vexnum; i++)G->Vexs[i] = v[i];//初始化图的边权int start_vex[8] = { 0,0,1,1,2,2,2,3 };int end_vex[8] = { 1,3,2,3,0,1,3,2 };int vex_weight[8] = { 5,7,4,2,3,3,2,1 };for (int i = 0; i < G->arcnum; i++)G->Edges[start_vex[i]][end_vex[i]] = vex_weight[i];return G;
}/* 初始化路径矩阵 */
Path InitPath() {Path path;path.length = 0;return path;
}/* Floyd算法寻找最短路径 */
void Floyd(MGraph* Graph, Path *path) {int i, j, k, nun = Graph->vexnum;int temp[SIZE][SIZE];// 初始化for (i = 0; i < nun; i++) {for (j = 0; j < nun; j++) {temp[i][j] = Graph->Edges[i][j];path->path[i][j] = -1;}}// 算法主体for (k = 0; k < nun; k++) {for (i = 0; i < nun; i++) {for (j = 0; j < nun; j++) {if (temp[i][j] > temp[i][k] + temp[k][j]) {temp[i][j] = temp[i][k] + temp[k][j];path->path[i][j] = k;}}}}
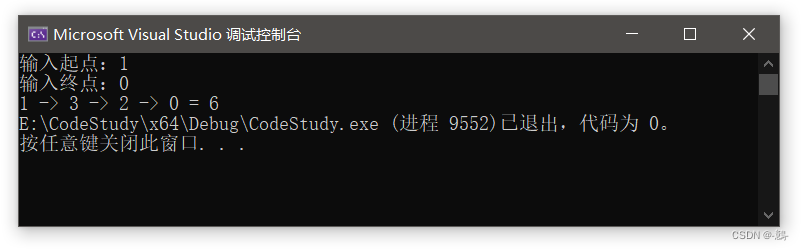
}三、运行结果
main方法代码如下:
int main() {MGraph* Graph = InitGraph();Path path = InitPath();Floyd(Graph, &path);PrintPath(Graph, &path);return 0;
}
四、源代码
#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>#define SIZE 4 //邻接矩阵大小(v0 - v3)
#define MaxNum 999 //不可到达点的权值(即无穷大)typedef int VertexType;
typedef int EdgeType;/*图*/
typedef struct {VertexType Vexs[SIZE]; //结点 EdgeType Edges[SIZE][SIZE]; //权值 int vexnum, arcnum;
}MGraph;/*路径*/
typedef struct {int path[SIZE][SIZE];EdgeType length;
}Path;/* 初始化图并输入权值 */
MGraph* InitGraph() {MGraph* G = (MGraph*)malloc(sizeof(MGraph));G->vexnum = 4;G->arcnum = 8;//初始化图的邻接矩阵 Edges[SIZE][SIZE]for (int i = 0; i < G->vexnum; i++) {for (int j = 0; j < G->vexnum; j++) {if (i == j) G->Edges[i][j] = 0; //对角线权值为0 else G->Edges[i][j] = MaxNum; //除对角线外所有权值为无穷大 }}//初始化图的结点矩阵 Vexs[SIZE]VertexType v[4] = { 0,1,2,3 };for (int i = 0; i < G->vexnum; i++)G->Vexs[i] = v[i];//初始化图的边权int start_vex[8] = { 0,0,1,1,2,2,2,3 };int end_vex[8] = { 1,3,2,3,0,1,3,2 };int vex_weight[8] = { 5,7,4,2,3,3,2,1 };for (int i = 0; i < G->arcnum; i++)G->Edges[start_vex[i]][end_vex[i]] = vex_weight[i];return G;
}/* 初始化路径矩阵 */
Path InitPath() {Path path;path.length = 0;return path;
}/* Floyd算法寻找最短路径 */
void Floyd(MGraph* Graph, Path *path) {int i, j, k, nun = Graph->vexnum;int temp[SIZE][SIZE];// 初始化for (i = 0; i < nun; i++) {for (j = 0; j < nun; j++) {temp[i][j] = Graph->Edges[i][j];path->path[i][j] = -1;}}// 算法主体for (k = 0; k < nun; k++) {for (i = 0; i < nun; i++) {for (j = 0; j < nun; j++) {if (temp[i][j] > temp[i][k] + temp[k][j]) {temp[i][j] = temp[i][k] + temp[k][j];path->path[i][j] = k;}}}}
}/* 递归寻找最短路径 */
void FindPath(int start, int end, Path* path, MGraph* Graph) {if (path->path[start][end] == -1) {printf("-> %d ", end);path->length = path->length + Graph->Edges[start][end];}else {int mid = path->path[start][end];FindPath(start, mid, path, Graph);FindPath(mid, end, path, Graph);}
}/* 打印最短路径 */
void PrintPath(MGraph* Graph, Path* path) {VertexType start, end;printf("输入起点:");scanf("%d", &start);printf("输入终点:");scanf("%d", &end);printf("%d ", start);FindPath(start, end, path, Graph);printf("= %d", path->length);
}int main() {MGraph* Graph = InitGraph();Path path = InitPath();Floyd(Graph, &path);PrintPath(Graph, &path);return 0;
}