GaN HEMT器件的大信号等效电路模型分为经验基模型和物理基模型。经验基模型具有较高精度但参数提取困难,特别在GaN HEMT器件工艺不稳定的情况下不易应用。相比之下,物理基模型从器件工作机理出发,参数提取相对方便,且更容易更新和维护。在GaN HEMT器件标准化过程中,选择了基于表面势和基于电荷控制的物理基大信号模型。然而,这些模型仍存在方程复杂、收敛性差、精度不足等问题。基于区域划分的可缩放大信号模型,兼顾了简单性和精度,并考虑了自热效应、高低温效应、陷阱效应等。该模型在不同栅宽的GaN HEMT器件上得到了验证,显示出良好的小信号和大信号性能。
区域划分建模原理
区域划分建模方法是一种基于器件沟道中电场和载流子分布的模拟方法,将沟道划分为相邻的区域。在每个区域内,使用相应的物理方程描述电流-电压关系,考虑器件的主要工作原理。通过确保电流、电压、电场等物理量在各区域边界的连续性,将各区域的方程联立求解,得到器件的最终I-V特性。
该建模方法最早在20世纪80年代应用于MODFET器件的建模。随着第三代半导体材料和器件的发展,这种建模方法在21世纪初开始用于AlGaN/GaN HFET器件。从2006年起,美国北卡罗来纳州立大学的Robert Trew团队对区域划分模型进行了深入研究,并提出了可用于大信号仿真的区域划分大信号模型。这一模型结合了物理基模型和经验基模型的优势,既反映了器件的物理机理,又能够集成于电路仿真软件中进行大信号谐波平衡仿真。从理论上讲,这种模型在器件和电路的设计与分析中都具有应用前景。以下对区域划分建模原理进行简要介绍。
依据器件工作时沟道中电场和载流子的分布,可以将沟道划分为不同的区域。
器件工作于线性区:
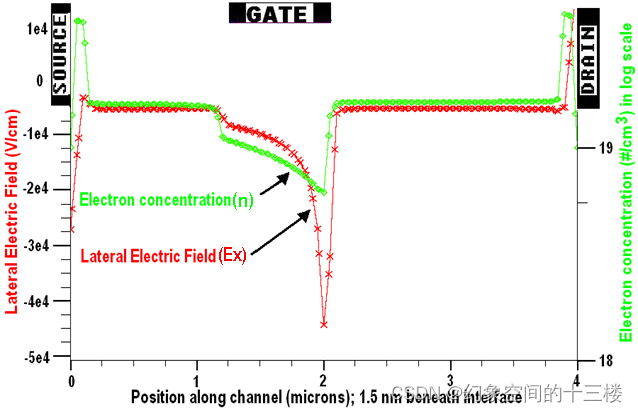
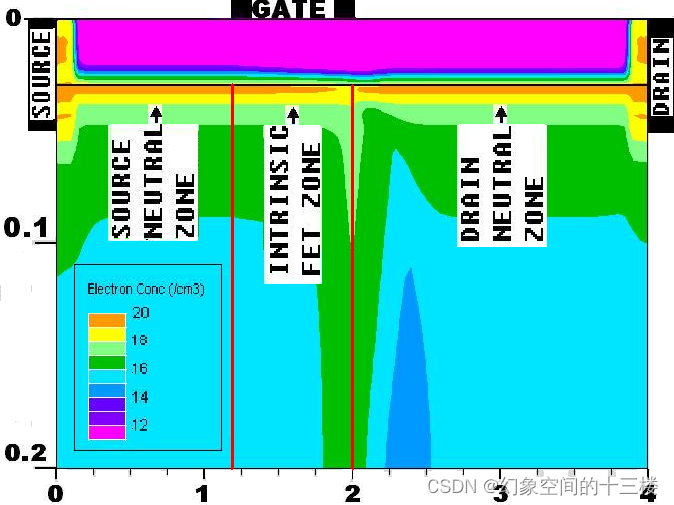
在线性区可以将器件划分为三个区域,分别是源极接入区(Source Neutral Zone,SNZ, Z1);占据栅下全部区域的本征FET区(Intrinsic FET Zone,IFZ, Z2)和漏极接入区 (Drain Neutral Zone,DNZ, Z5)。
器件工作于饱和区:
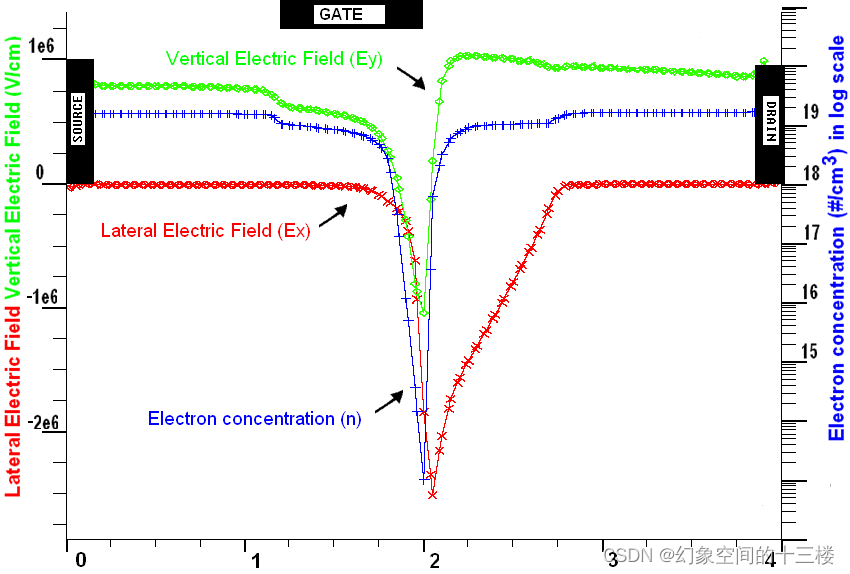
在饱和区,可以将器件划分为五个区域。分别是源极接入区 (SNZ, Z1);占据栅下源端部分区域的本征接入区(IFZ, Z2) ; 占据栅下剩余部分的空间电荷聚集区(Space-charge Limited Zone,SLZ, Z3);占据始于栅极漏端的部分漏极接入区的电荷耗尽区(Charge Deficit Zone,CDZ, Z4)和漏极接入区 (Drain Neutral Zone,DNZ,Z5)。
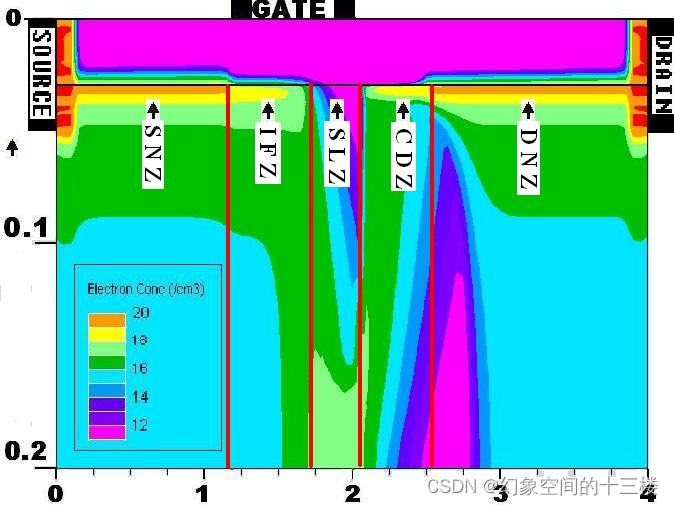
当器件工作于线性区时,在源极接入区和漏极接入区,量子阱被电子填满,电子速度最小。在本征FET区,电子漂移速度增加,但仍小于电子饱和速度vsat。在源极接入区和漏极接入区,由电场-电子速度关系可得:
ν = μ E ( 1 + ( E / E c ) β ) 1 / β ( 1 ) \nu=\frac{\mu E}{\left(1+\left(E/E_c\right)^{\beta}\right)^{1/\beta}}(1) ν=(1+(E/Ec)β)1/βμE(1)、
由(1)式可得:
E = E c ( 1 − ( ν s a t / ν ) β ) 1 / β ( 2 ) E=\frac{E_c}{(1-(\nu_{\mathrm{sat}}/\nu)^\beta)^{1/\beta}}(2) E=(1−(νsat/ν)β)1/βEc(2)
其中μ为低场电子迁移率,Ec为电子速度饱和时的临界电场,vsat为电子饱和速度,β为电场-电子速度关系的阶数,通常β = 2。
这里的β为拟合值
由式(2)可进一步得到源极接入区和漏极接入区的电场如下:
E s = E c I I s a t β − I β β ( 3 ) E_s=\frac{E_cI}{\sqrt[\beta]{I_{sat}^\beta-I^\beta}}(3) Es=βIsatβ−IβEcI(3)
其中Isat为饱和电流。根据器件工作在线性区时沟道中电场的分布,电场在源极接入区和漏极接入区可被视为常数,可以根据电场与电势的关系,得到栅极源端和栅极漏端的电压如下:
V s i = E c l s I ( I s a t β − I β ) 1 / β ( 4 ) V_{si}=\frac{E_{c}l_{s}I}{\left(I_{sat}^{\beta}-I^{\beta}\right)^{1/\beta}}(4) Vsi=(Isatβ−Iβ)1/βEclsI(4)
这里的I应为Isi(Z1中电流的解析解),参考原式:
V s i = E c L s I s i ( I max β − I s i β ) 1 / β . V_{si}=\frac{E_{c}L_{s}I_{si}}{\left(I_{\max}^{\beta}-I_{si}^{\beta}\right)^{1/\beta}}. Vsi=(Imaxβ−Isiβ)1/βEcLsIsi.
V d i = V d − E c l d I ( I s a t β − I β ) 1 / β ( 5 ) V_{di}=V_d-\frac{E_cl_dI}{\left(I_{sat}^\beta-I^\beta\right)^{1/\beta}}(5) Vdi=Vd−(Isatβ−Iβ)1/βEcldI(5)
这里的I应为Ids,参考原式:
V d i = V d − E c ( L d − L 4 ) I d s ( I max β − I d s β ) 1 / β − 1 2 L 4 2 k 4 , V_{di}=V_d-\frac{E_c(L_d-L_4)I_{ds}}{\left(I_{\max}^\beta-I_{ds}^\beta\right)^{1/\beta}}-\frac12L_4^2k_4, Vdi=Vd−(Imaxβ−Idsβ)1/βEc(Ld−L4)Ids−21L42k4,
其中 Vsi 和 Vdi 分别为栅极源端和栅极漏端的电压,ls 和ld 分别为源极接入区和漏极接入区的长度,Vd 为漏极偏置电压。
在本征FET 区,根据缓变沟道近似,载流子浓度满足如下关系:
n s ( x ) = C e f f q ( V g t − V ( x ) ) ( 6 ) n_s(x)=\frac{C_{eff}}q(V_{gt}-V(x))(6) ns(x)=qCeff(Vgt−V(x))(6)
其中ns(x)为位置x 处的载流子浓度,Ceff 为有效势垒电容,Vgt =Vgs - Vpinch,V(x)为位置 x 处的电势。将式(1),(6)两式和电场与电势的关系E(x)= -dV/dx 代入漏极电流Ids 的基本表达式:
I d s = W q n s ( x ) ν ( x ) ( 7 ) I_{ds}=Wqn_s(x)\nu(x)(7) Ids=Wqns(x)ν(x)(7)
其中W 为器件的栅宽,q 为电子电荷,v(x)为位置x 处的电子速度。整理后,可得漏极电流Ids 的表达式如下:
( x − l s ) I d s = ∫ V s i V ( x ) ( ( W μ C e f f ( V g t − V ′ ) ) β − ( I d s E c ) β ) 1 / β d V ′ ( 8 ) \left.(x-l_s)I_{ds}=\int_{V_{si}}^{V(x)}\left(\begin{array}{c}(W\mu C_{eff}\left(V_{gt}-V^{\prime}\right))^{\beta}-(\frac{I_{ds}}{E_{c}})^{\beta}\\\end{array}\right.\right)^{1/\beta}dV^{\prime}(8) (x−ls)Ids=∫VsiV(x)((WμCeff(Vgt−V′))β−(EcIds)β)1/βdV′(8)
将式(8)在栅下整个区域积分,则式(8)可化为如下形式:
l g I d s = ∫ V s i V d i ( ( W μ C e f f ( V g t − V ) ) β − ( I d s E c ) β ) 1 / β d V ( 9 ) {l}_gI_{ds}=\int_{V_{si}}^{V_{di}}\left(\left(W\mu {C}_{eff}\left(V_{gt}-V\right)\right)^\beta-\left(\frac{I_{ds}}{E_{c}}\right)^\beta\right)^{1/\beta}dV(9) lgIds=∫VsiVdi((WμCeff(Vgt−V))β−(EcIds)β)1/βdV(9)
其中lg 为栅长。再将式(4)和式(5)中的Vsi 和Vdi 代入式(9),求解该积分方程,即可得到器件工作于线性区时的漏极电流Ids。
以上式子中需要实际测试的物理量有:
(4)式中需要测试的物理量
| 需要测试的量 | 含义 |
|---|---|
| Ec | 电子速度饱和时的临界电场 |
| ls | 源极接入区长度 |
| Isat | 电流比例因子 |
(5) 式中需要测试的物理量
| 需要测试的量 | 含义 |
|---|---|
| Ec | 电子速度饱和时的临界电场 |
| Vd | 漏极偏置电压 |
| ld | 漏极接入区的长度 |
(9)式中需要测试的物理量
| 需要测试的量 | 含义 |
|---|---|
| lg | 栅长 |
| W | 栅宽 |
| Ceff | 有效势垒电容 |
| Vgt | 有效栅极电压 |
| Ec | 电子速度饱和时的临界电场 |
以上式子中需要拟合的量有:
β 电场-电子速度关系的阶数