算法刷题-动态规划2
- 珠宝的最高价值
- 下降路径最小和
- 使用最小花费爬楼梯
- 整数拆分
珠宝的最高价值
题目

大佬思路
多开一行使得代码更加的简洁
移动到右侧和下侧
dp[ i ][ j ]有两种情况:
第一种是从上面来的礼物最大价值:dp[ i ][ j ] = dp[ i - 1 ][ j ] + g[ i ][ j ]
第二种是从左面来的礼物最大价值:dp[ i ][ j ] = dp[ i ][ j - 1 ] + g[ i ][ j ]
所以得出状态表达式,dp[ i ][ j ] = max( dp[ i ][ j - 1 ],dp[ i - 1 ][ j ] ) + g[ i ][ j ]
2。为了简洁代码,多增加一行
class Solution {public int maxValue(int[][] grid) {int m = grid.length;int n = grid[0].length;//dp[i][j]表示从grid[0][0]到grid[i - 1][j - 1]时的最大价值int[][] dp = new int[m + 1][n + 1];for (int i = 1; i <= m; i++) {for (int j = 1; j <= n; j++) {dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n];}
}class Solution {
public: int maxValue(vector<vector<int>>& grid) { int m = grid.size(), n = grid[0].size(); vector<vector<int>> dp(m + 1, vector<int>(n + 1)); for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]) + grid[i - 1][j - 1];}}return dp[m][n]; }
};
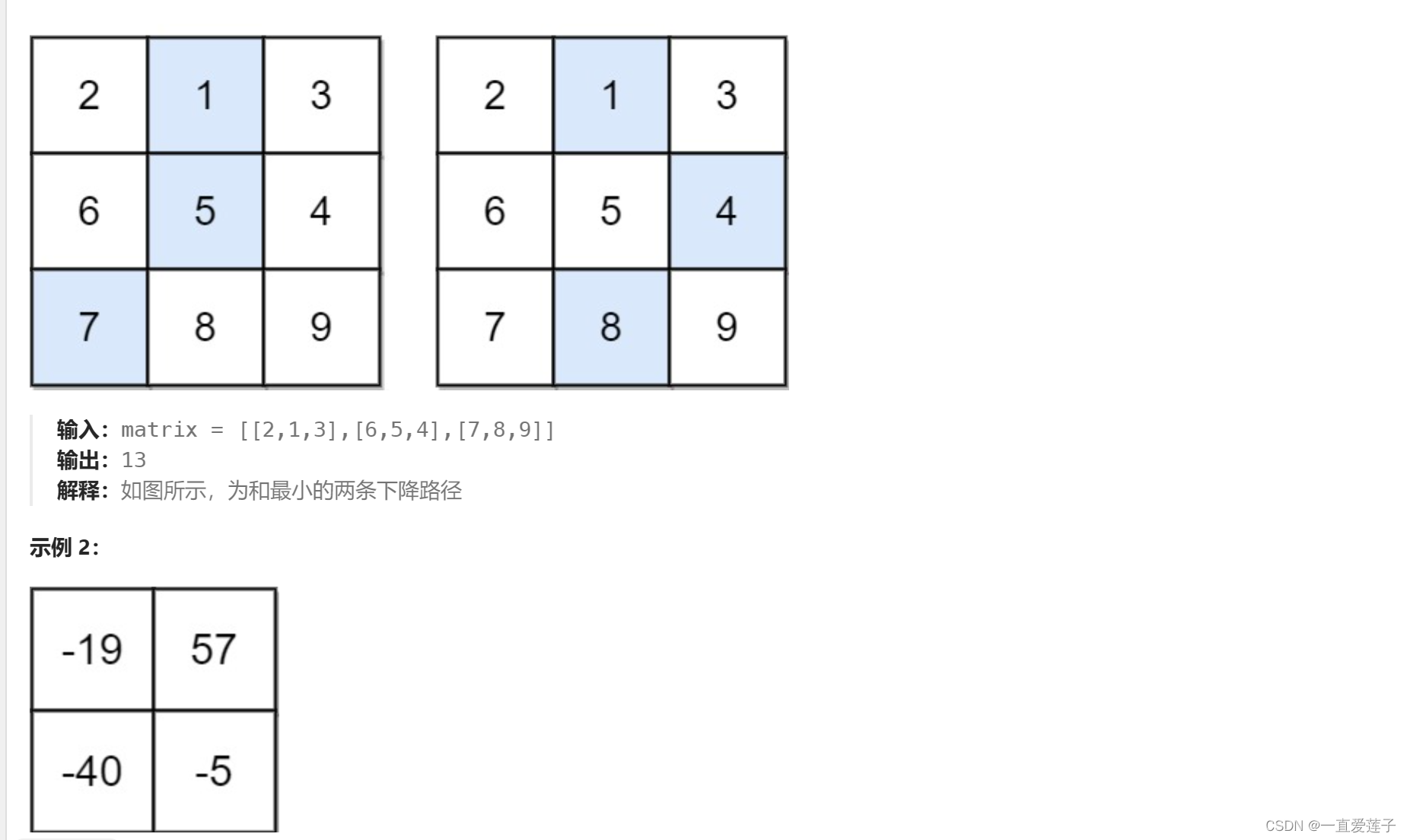
下降路径最小和


头文件: #include< algorithm >
返回值: 两个函数返回的都是迭代器,所以要提取数值的话需要在函数前加上*
语法格式: max_element(first,end,cmp);其中cmp为可选择参数(自定义排序可用,默认不需要填)
两个函数默认都是从小到大排列, max_element() 输出最后一个值, min_element() 输出第一个值。
这里要特别注意:如果自定义排序是从大到小的, max_element() 和min_element() 的返回结果相反,也就是说max_element()返回的是最小值,min_element()返回的是最大值 。
- 定义函数dp[i][j] ,是关于路径到达 i,j 点的最小值
- 然后找 关系式,分析最后一点是从哪里得到的, 从左上方来:dp[ i - 1 ][ j - 1 ] + m[ i ][ j ],从正上方来:dp[ i - 1 ][ j ] + m[ i ][ j ], 从右上方来:dp[ i - 1 ][ j + 1 ] + m[ i ][ j ]
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int n = matrix.size();vector<vector<int>> dp(n, vector<int>(n));copy(matrix[0].begin(), matrix[0].end(), dp[0].begin());for (int i = 1; i < n; i++) {for (int j = 0; j < n; j++) {int mn = dp[i - 1][j];if (j > 0) {mn = min(mn, dp[i - 1][j - 1]);}if (j < n - 1) {mn = min(mn, dp[i - 1][j + 1]);}dp[i][j] = mn + matrix[i][j];}}return *min_element(dp[n - 1].begin(), dp[n - 1].end());}
//INT_MAX = 2 ^ 31 - 1,INT_MIN = -2 ^ 31.
//防止越界,在左边,上面和右边都增加一行
//并且将第一行定义为0
class Solution {
public:int minFallingPathSum(vector<vector<int>>& matrix) {int m = matrix.size(), n = matrix[0].size();vector<vector<int>> dp(m + 1, vector<int>(n + 2, INT_MAX));for (auto& e : dp[0]) e = 0; for (int i = 1; i <= m; i++) { for (int j = 1; j <= n; j++) { dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1]))+ matrix[i - 1][j - 1]; }}int ans = INT_MAX; for (const auto& k : dp[m]) ans = min(ans, k); return ans; }
};
使用最小花费爬楼梯
题目
使用递归操作的几个步骤
1.明确dp[]函数的含义
2.明确关系式
3.进行初始化操作
4.确定遍历操作

class Solution {//本题是要求跳到最后一个台阶+1的位置public int minCostClimbingStairs(int[] cost) { int len = cost.length; //dp表示停留在第i个台阶上的花费 int[] dp = new int[len + 1]; //可以从第一个或第0个台阶起跳 dp[0] = 0; dp[1] = 0; //到达第i个台阶要么是从dp[i-2]跳两个台阶上来,要么从do[i-1]跳一个台阶上来 for (int i = 2; i <= len; i++) { dp[i] = Math.min(dp[i - 2] + cost[i - 2], dp[i - 1] + cost[i - 1]);}return dp[len]; }
整数拆分
题目

递归操作
1.确定dp数组含义
dp[i]:分拆数字i,可以得到的最大乘积为dp[i]
2.明确关系式
3.数组初始化
4.遍历顺序
大佬讲解
(无敌解释)
class Solution {
public:/*** 1. 确定dp数组下标含义 分拆数字i,可以得到的最大乘积为dp[i];* 2. 递推公式 dp[i] = max(dp[i], (i - j) * j, dp[i - j] * j);* 3. 初始化 dp[2] = 1;* 4. 遍历顺序 从前向后遍历就可以;* 5. 推导结果;*/int integerBreak(int n) {/* 定义dp数组 */vector<int> dp(n + 1);/* dp数组初始化 */dp[2] = 1;/* 从前向后遍历 */for (int i = 3; i <= n ; i++) {/* j遍历到小于i的值 */for (int j = 1; j < i - 1; j++) {dp[i] = max(dp[i], max((i - j) * j, dp[i - j] * j));}}return dp[n];}
};