动态规划
139. 单词拆分(一维)
给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true
解释: 返回 true 因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”]
输出: true
解释: 返回 true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20
s 和 wordDict[i] 仅由小写英文字母组成
wordDict 中的所有字符串 互不相同
class Solution {
public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordDictSet;for (auto word: wordDict) {wordDictSet.insert(word);}auto dp = vector<bool>(s.size()+1);dp[0] = true;for (int i = 1; i <= s.size(); ++i) {for (int j = 0; j < i; j++) {if (dp[j] && wordDictSet.find(s.substr(j, i-j)) != wordDictSet.end()) {dp[i] = true;break;}}}return dp[s.size()];}
};
343. 整数拆分
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
class Solution {
public:int integerBreak(int n) {if (n <= 3) {return n-1;}vector <int> dp(n+1);dp[2] = 1;for (int i = 3; i <= n; i++) {dp[i] = max(max(2 * (i - 2), 2 * dp[i - 2]), max(3 * (i - 3), 3 * dp[i - 3]));}return dp[n];}
};
96. 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:

输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
class Solution {
public:int numTrees(int n) {vector<int> dp(n+1, 0);dp[0] = 1;dp[1] = 1;for (int i = 2; i < n+1; i++) {for (int j = 1; j <= i; j++){dp[i] = dp[i]+(dp[j-1]*dp[i-j]);}}return dp[n];}
};
62. 不同路径
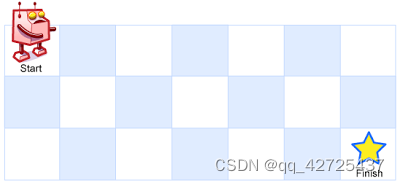
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向下 -> 向下
- 向下 -> 向下 -> 向右
- 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
class Solution {
public:int uniquePaths(int m, int n) {vector<vector<int>> f(m, vector<int>(n));for (int i = 0; i < m; ++i) {f[i][0] = 1;}for (int j = 0; j < n; ++j) {f[0][j] = 1;}for (int i = 1; i < m; ++i) {for (int j = 1; j < n; ++j) {f[i][j] = f[i - 1][j] + f[i][j - 1];}}return f[m - 1][n - 1];}
};
5. 最长回文子串
给你一个字符串 s,找到 s 中最长的回文子串。
如果字符串的反序与原始字符串相同,则该字符串称为回文字符串。
示例 1:
输入:s = “babad”
输出:“bab”
解释:“aba” 同样是符合题意的答案。
示例 2:
输入:s = “cbbd”
输出:“bb”
class Solution {
public:string longestPalindrome(string s) {int n = s.size();if (n < 2) {return s;}int maxLen = 1;int begin = 0;// dp[i][j] 表示 s[i..j] 是否是回文串vector<vector<int>> dp(n, vector<int>(n));// 初始化:所有长度为 1 的子串都是回文串for (int i = 0; i < n; i++) {dp[i][i] = true;}// 递推开始// 先枚举子串长度for (int L = 2; L <= n; L++) {// 枚举左边界,左边界的上限设置可以宽松一些for (int i = 0; i < n; i++) {// 由 L 和 i 可以确定右边界,即 j - i + 1 = L 得int j = L + i - 1;// 如果右边界越界,就可以退出当前循环if (j >= n) {break;}if (s[i] != s[j]) {dp[i][j] = false;} else {if (j - i < 3) {dp[i][j] = true;} else {dp[i][j] = dp[i + 1][j - 1];}}// 只要 dp[i][L] == true 成立,就表示子串 s[i..L] 是回文,此时记录回文长度和起始位置if (dp[i][j] && j - i + 1 > maxLen) {maxLen = j - i + 1;begin = i;}}}return s.substr(begin, maxLen);}
};