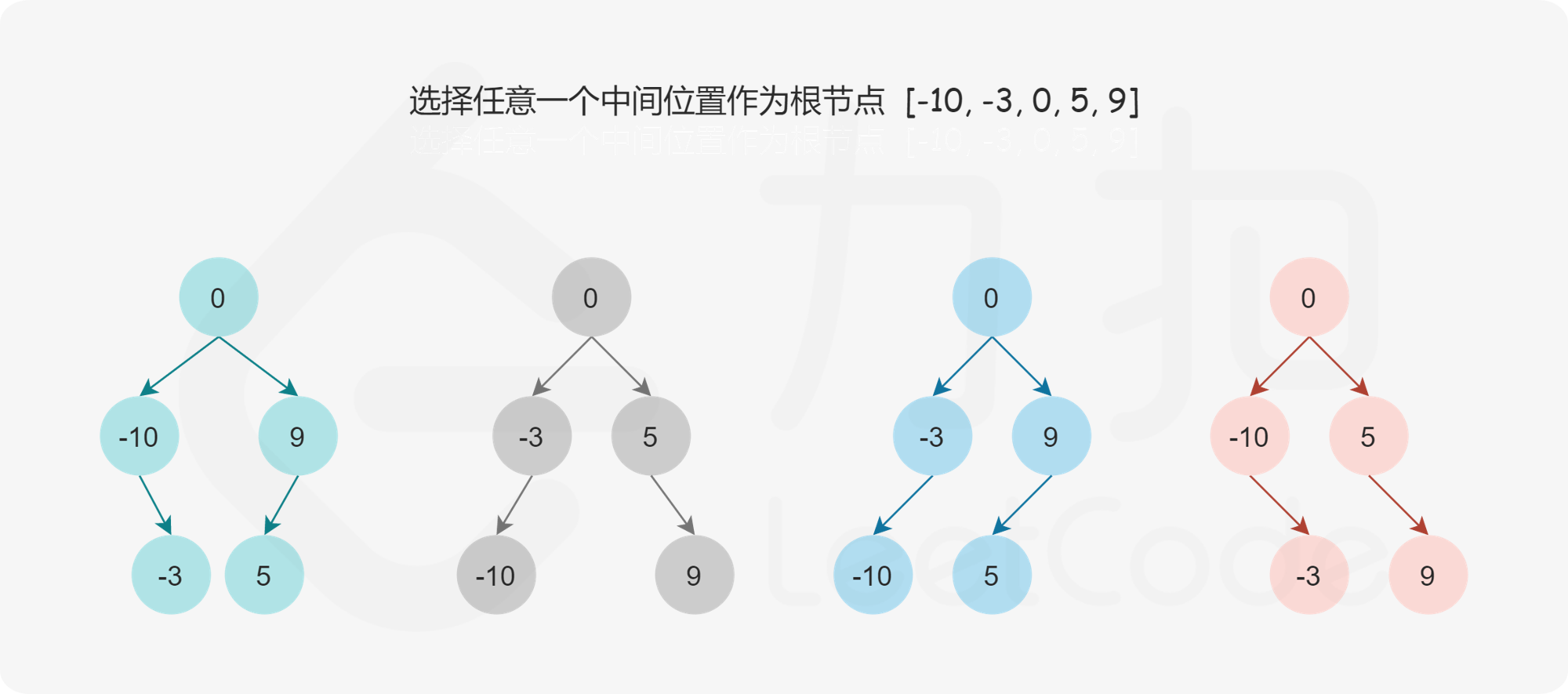
目录
前言
建堆的时间复杂度
向上调整建堆的时间复杂度
向下调整建堆的时间复杂度
维护堆的时间复杂度
top K问题的时间复杂度
前言
在前面的三篇文章中我们成功的实现了堆排序的升降序以及基于堆的top K问题,现在我们来解决它们的时间复杂度问题
建堆的时间复杂度
关于建堆的时间复杂度计算我们放在了:大小堆的实现(C语言)中讲解
向上调整建堆的时间复杂度

计算方式:此时所处层的结点个数 * 向上调整次数
文字描述: 假设我们有一个具有 N 个节点的满二叉树,并且我们正在对其中某个节点进行向上调整。在最坏情况下,该节点可能需要一直交换到根节点位置才能满足堆性质。
公式描述:
向上调整建堆到叶子结点时就不再调整,假设向下调整建堆的累计调整次数是T(h),那么:
T(h) = 2^1 * 1 + 2^2 * 2 + ...... + 2^(h-2) * (h-2) + 2^(h-1) * (h-1) ①
2*T(h) = 2^2 * 1 + 2^3 * 2 + ...... + 2^(h-1) * (h-2) + 2^h * (h-1) ②由②-①得:
T(h) = -(2^0 + 2^1 + 2^2 + ...... + 2^(h-2) + 2^(h-1)) + 2^h*(h-1) + 2^0 ③
由等比数列求和公式得:
T(h) = -((2^h) - 1) + 2^h*(h-1) + 2^0 ④
又由于满二叉树高度h与总结点个数N之间的关系是h = log(N+1),故将④化简可得:
T(N) = -N + (N+1)(log(N+1)-1) + 1
因此,向上调整建堆的时间复杂度为:O(N*logN)
向下调整建堆的时间复杂度
假设该堆为满二叉树,此时向下调整的情况是最坏的情况:
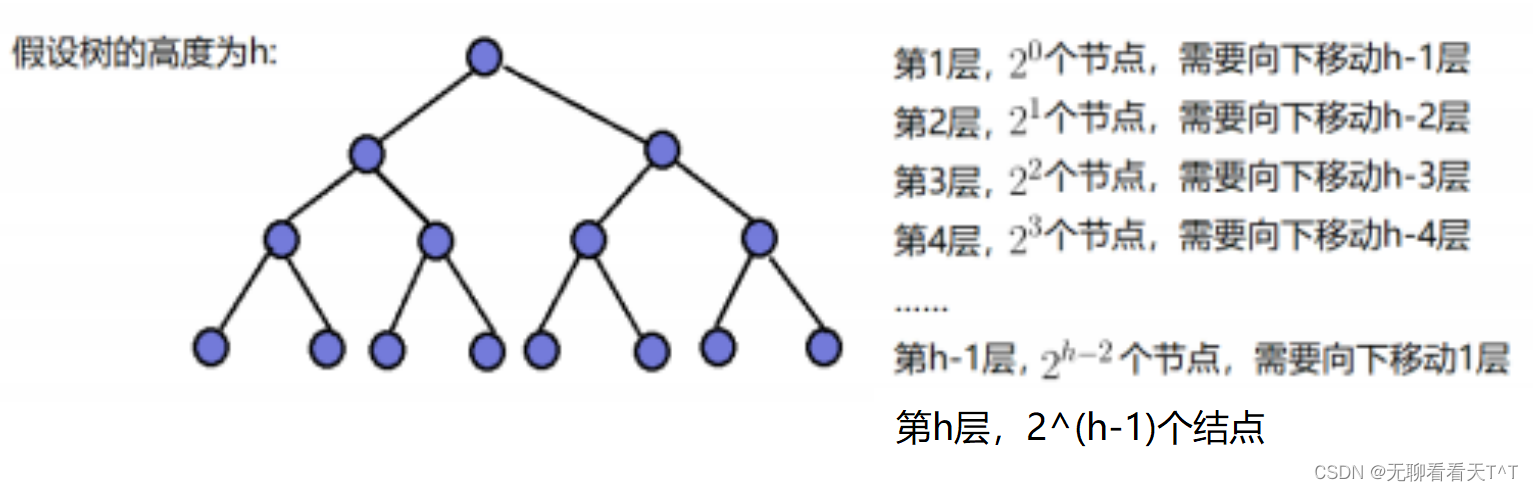
计算方式:此时所处层的结点个数 * 向下调整次数
文字描述:假设有一个具有 N 个元素的完全二叉树(即堆),其中 h 是该二叉树的高度。在最坏情况下,需要将一个元素从根节点向下移动到底部层次,并且每一次都需要与其子节点进行比较和交换操作。
公式描述:
向下调整建堆到叶子结点时就不再调整,假设向下调整建堆的累计调整次数是T(h),那么:
T(h) = 2^(h-2) * 1 + 2^(h-3) * 1 + ...... + 2^1 * (h-2) + 2^0 * (h-1) ①
2*T(h) = 2^(h-1) * 1 + 2^(h-2) * 1 + ...... + 2^2 * (h-2) + 2^1 * (h-1) ②由②-①得:
T(h) = 2^(h-1) + 2^(h-2) + ...... + 2^1 + 2^0 - h ③
由等比数列求和公式得:
T(h) = 2^h - 1 -h ④
又由于满二叉树高度h与总结点个数N之间的关系是h = log(N+1),故将④化简可得:
T(N) = N - log(N+1)
因此,向下调整建堆的时间复杂度为:O(N)
结论:向下调整建堆的时间复杂度为O(N),向上调整建堆的时间复杂度为O(N*logN),因此更倾向于使用向下调整的方式建堆
向下调整与向下调整建堆的时间复杂度分别为O(logN)与O(N)
维护堆的时间复杂度
//维护
int end = n - 1;
while (end > 0)
{Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;
}
维护堆的时间复杂度为O(N*logN)

文字描述:
假设数组
a的长度为n,则循环会执行n-1次迭代,每次迭代都包括以下几个步骤:
交换首尾元素:通过调用 Swap 函数交换数组首尾元素,所需时间复杂度为 O(1)
向下调整:向下调整的时间复杂度为O(logN)
更新结束标志:将结束标志
end减一,表示缩小待处理区间,所需时间复杂度为 O(1)因此,时间复杂度O(n) = (N-1)logN = N*logN
公式描述:
在满二叉树中的总结点个数N为:
N = (2^0) + (2^1) + ... + 2^(h-1)由等比数列求和公式得到:
N = (2^h - 1)因此堆高度 h 与结点总数N的关系为:
h = log(N + 1)最坏情况下,一个元素需要一直向下移动到叶子节点,此时它经过堆高度上所有层级:
所以时间复杂度为O(logN)
补充:时间复杂度计算的是输入规模与算法最坏执行时间之间的关系,在向下调整操作中,时间复杂度计算了堆的总结点个数 N 与一个结点最坏的调整次数所需的时间,这个时间又与结点的高度h有关而h=log(N+1),所以O(N) = log(N+1) = log(N)
top K问题的时间复杂度
文字描述:
利用堆解决top K问题可以分为两个阶段:
建立初始大小为 K 的最小堆:需要插入 K 个元素到空的初始堆中。每次插入操作都需要执行一次向上调整操作,时间复杂度为 O(logK)
因此,在建立初始大小为 K 的最小堆时所需总比较和交换次数是 O(KlogK)处理剩余 N-K 个元素:对于每个剩余元素,如果它大于当前最小值(即根节点),则替换并执行向下调整操作,以维护最新的 top k 元素,每次替换和向下调整都需要花费 O(logK) 的时间。
因此,在处理剩余 N-K 个元素时所需总比较和交换次数是 O((N-K)logK)因此,使用堆解决 Top K 问题的时间复杂度为 O(KlogK + (N-K)logK),其中 N 是输入元素的总数。如果 K 远小于 N,则该算法的时间复杂度可近似为 O(NlogK),因为 K 的值相对较小可忽略不计。
~over~