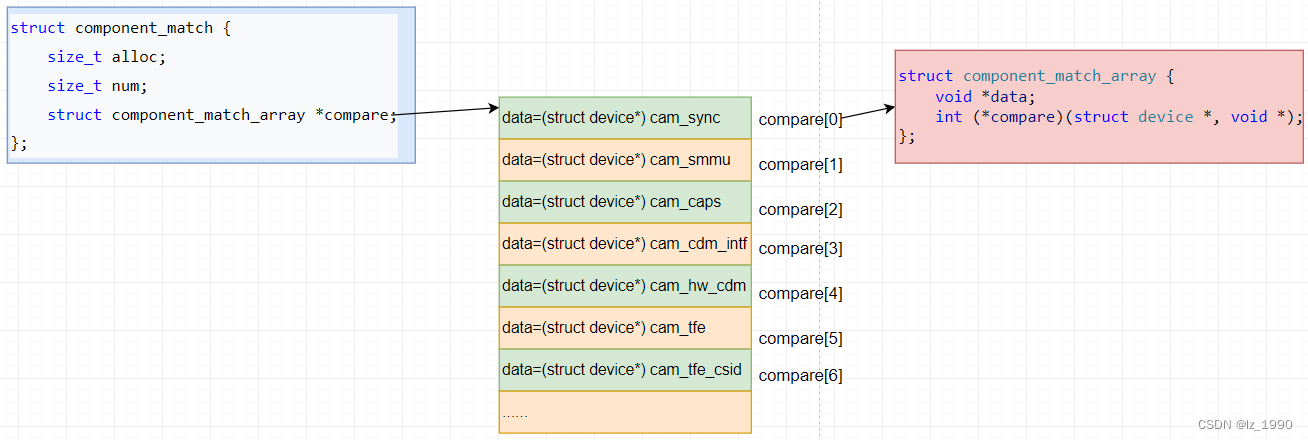
ReLU(Rectified Linear Unit)和Sigmoid都是神经网络中常用的激活函数。

特点:
ReLU是一种简单而有效的激活函数。它对于正数部分直接返回输入,对于负数部分返回零。这种非线性转换有助于网络学习更复杂的表示。ReLU在许多深度学习模型中被广泛使用,因为它在梯度下降中的计算上相对简单,且有效防止了梯度消失问题。
Sigmoid函数将输入映射到(0,1)之间的范围,常用于二分类问题。它的输出可以解释为概率值,因此在输出层用于模型对样本属于某个类别的置信度。然而,Sigmoid函数在输入远离零时梯度接近零,可能导致梯度消失问题,尤其在深度网络中。
ReLU激活函数图:
- ReLU函数的图形是一条直线,在输入大于零时输出与输入相等,而在输入小于等于零时输出为零。

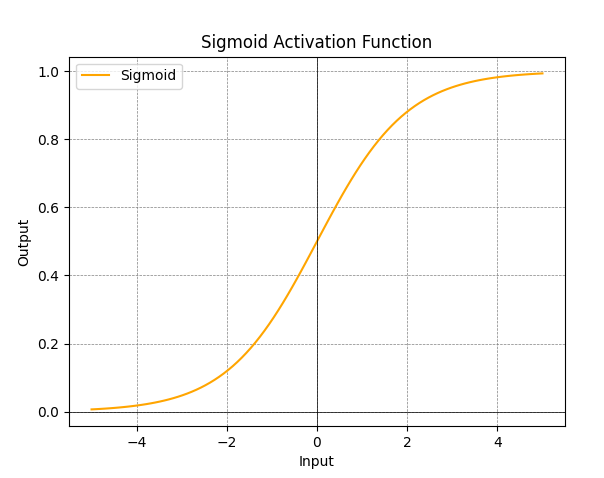
Sigmoid激活函数图:
- Sigmoid函数的图形是一条S形曲线,将输入映射到(0,1)范围内。
在实际使用中,ReLU常用于隐藏层,而Sigmoid常用于输出层(用于二分类任务)。随着研究的进展,有一些变体,如Leaky ReLU、Parametric ReLU、ELU等,旨在改进激活函数的性能。选择激活函数通常取决于具体的任务和网络结构。
![[NAND Flash] 3.1 闪存的组成结构原理与使用挑战](https://img-blog.csdnimg.cn/direct/a85eca0f4e874071b5cebc43aa8a2049.png#pic_center)