Leetcode 131 分割回文串-编程知识

Leetcode 131 分割回文串

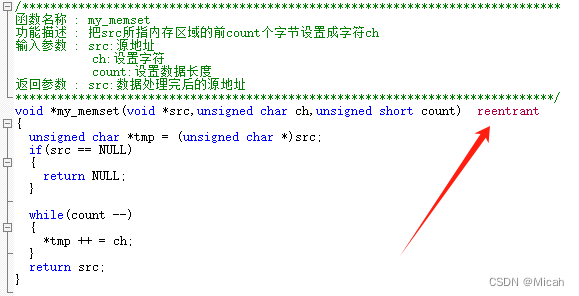
题意理解：

分割回文子串，可以看作是划分连续的字幕组合——所以也可以用回溯的方法来解决

每个位置选与不选——该位置切割|不切割

对于每一段子串——>判断是否是回文串：

是：继续切割

不是：剪枝

解题方法：

回溯，难点在于如何理解切割位置——将其抽象为树结构

切割位置：切割位置会比数组长度+1

1.暴力回溯+剪枝优化

准备条件：1.判断子串是回文？

2.递归|回溯

回溯三个关键步骤：

1.确定返回值和参数列表： void backtracking()

2.终止条件:

是回文且切至字符串尾部——结束，收集结果

3.单层逻辑|做好回溯步骤：

子串是不回文——剪枝：提前剪枝，所以分隔到字符串尾部的一定都是合法的回文分割。

 List<List<String>> result=new ArrayList<>();LinkedList<String> path=new LinkedList<>();public List<List<String>> partition(String s) {backtracking(s,0);return result;}public void backtracking(String s,int startIndex){//终止条件if(startIndex>=s.length()){result.add(new ArrayList<>(path));return;}//单层逻辑for(int i=startIndex;i<s.length();i++){//获取子串并判断if(isPalindrome(s,startIndex,i)){path.add(s.substring(startIndex,i+1));backtracking(s,i+1);path.removeLast();}else{//不是回文——剪枝continue;}}}//左闭右闭判断子串是否是回文public boolean isPalindrome(String s,int start,int end){while(start<=end){if(s.charAt(start)==s.charAt(end)){start++;end--;}else{return false;}}return true;}