文章目录

写在前面
二叉树的创建
二叉树的遍历
- 前序遍历
- 中序遍历
- 后序遍历
- 层序遍历
二叉树的销毁
二叉树节点个数
二叉树叶子节点的个数
二叉树查找值为x的节点
二叉树是否为完全二叉树

写在前面

二叉树的几乎所有实现都是依靠递归实现，递归的核心思路是把任何一个二叉树看成根和左右子树，而二叉树递归的核心玩法就是把二叉树的左右子树再看成根，再找左右子树，再看成根…

因此，解决二叉树问题实际上要把二叉树转换成一个一个子树的过程，找到一个一个的子树再组装起来就形成了二叉树

二叉树的创建

二叉树建立的正统方法是利用递归，这里展示递归的一种写法

BTNode* BuyNode(BTDataType a)
{BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));newnode->data = a;newnode->left = NULL;newnode->left = NULL;return newnode;
}BTNode* BinaryTreeCreate(BTDataType* a, int* pi)
{if (a[*pi] == '#'){(*pi)++;return NULL;}BTNode* root = BuyNode(a[*pi]);(*pi)++;root->left = BinaryTreeCreate(a, pi);root->right = BinaryTreeCreate(a, pi);return root;
}

如果你对递归的认识并不熟悉，下面我画了一幅递归展开图，更好解释这其中的原理

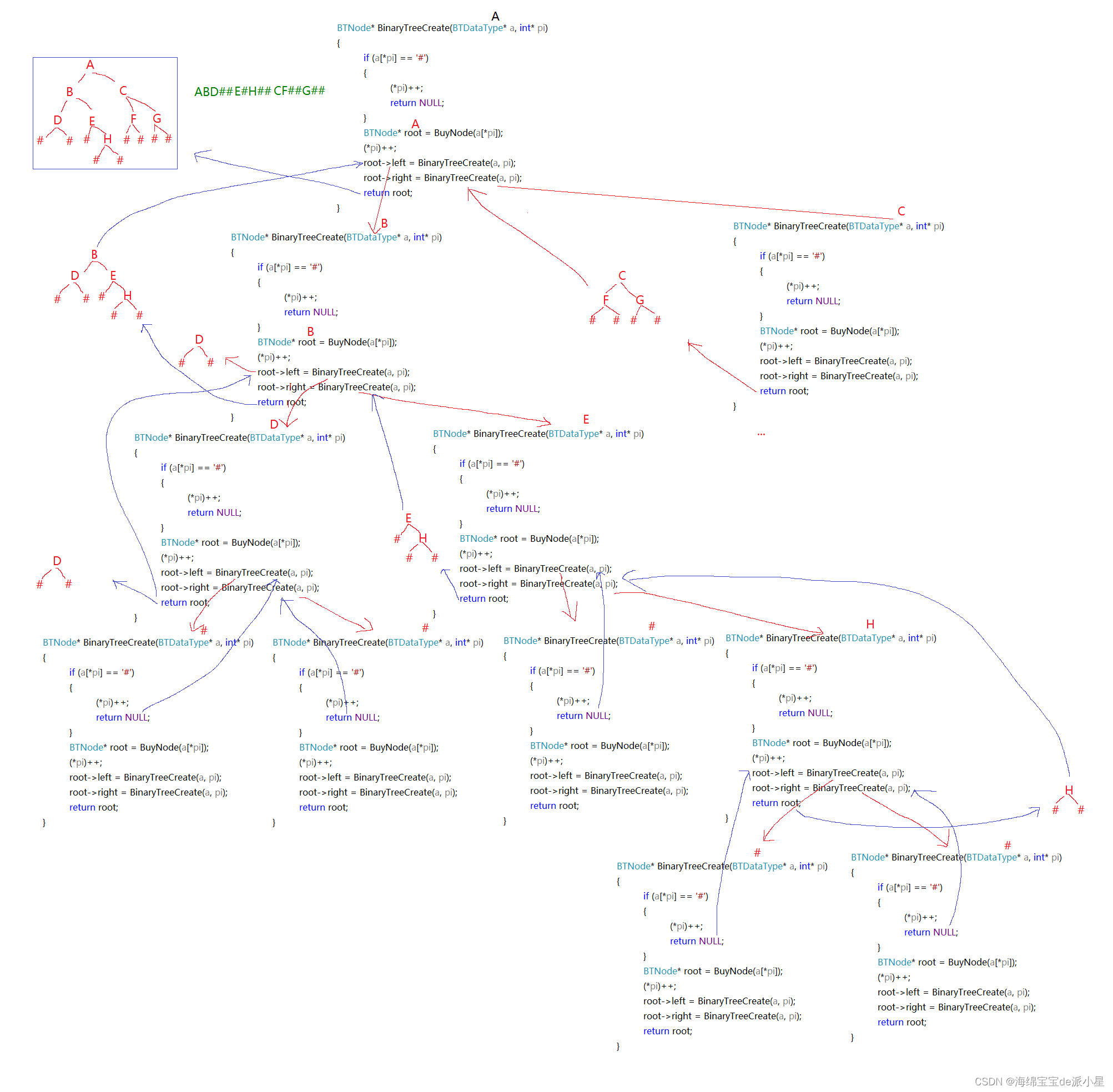
在这里插入图片描述
(右子树的部分过程由于空间原因不够完全展开，但如果看懂左子树的构建过程，右子树不难自己画出)

这里注意的是，函数栈帧的创建并不是每一个都不一样的位置，当一个栈帧被销毁后，另外一个栈帧创建就会在原来的位置，因此在计算空间复杂度的时候需要考虑这个问题：
空间是可以重复利用的，时间是一去不复返的

从这幅图中，相信可以理解这段代码的含义了

首先创建一个根节点，根节点去寻找左子树进入递归，而进入递归后继续寻找左子树…直到遇到NULL截止，而遇到空后就寻找右子树，右子树也找到空后返回，这样就构建出了二叉树中最小的一棵树，而这棵树会返回，作为根的左子树，然后继续进入递归寻找根的右子树…

由于是借助链表进行实现的，因此我们可以理解为首先创建好根，而根的左右子树用函数创建好后再连接起来…当遇到#就返回，形成了一个一个的小树，小树最后组成大树，就形成了二叉树

二叉树的遍历

二叉树的遍历主要有前序遍历，中序遍历，后序遍历，层序遍历

前序遍历

前序遍历是指遍历时先访问根，再访问左子树，再访问右子树

代码实现如下

void BinaryTreePrevOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%c ", root->data);BinaryTreePrevOrder(root->left);BinaryTreePrevOrder(root->right);
}

下面依旧画出它的递归展开图

在这里插入图片描述

中序遍历

中序遍历是先访问左子树，再访问根，最后访问右子树

void BinaryTreeInOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreeInOrder(root->left);printf("%c ", root->data);BinaryTreeInOrder(root->right);
}

递归图和上面基本类似，就不做画出了

后序遍历

后序遍历是先访问左子树，再访问右子树，最后访问根

void BinaryTreePostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}BinaryTreePostOrder(root->left);BinaryTreePostOrder(root->right);printf("%c ", root->data);
}

递归图和上面基本类似，就不做画出了

层序遍历

层序遍历指的是对二叉树进行一层一层的遍历，每一层分别遍历，这里借助队列进行遍历，基本思路把根放到队列中，当某一个根要出队列时，就令该根的左子树和右子树进队列，这样就能实现一层一层遍历，画法如下：

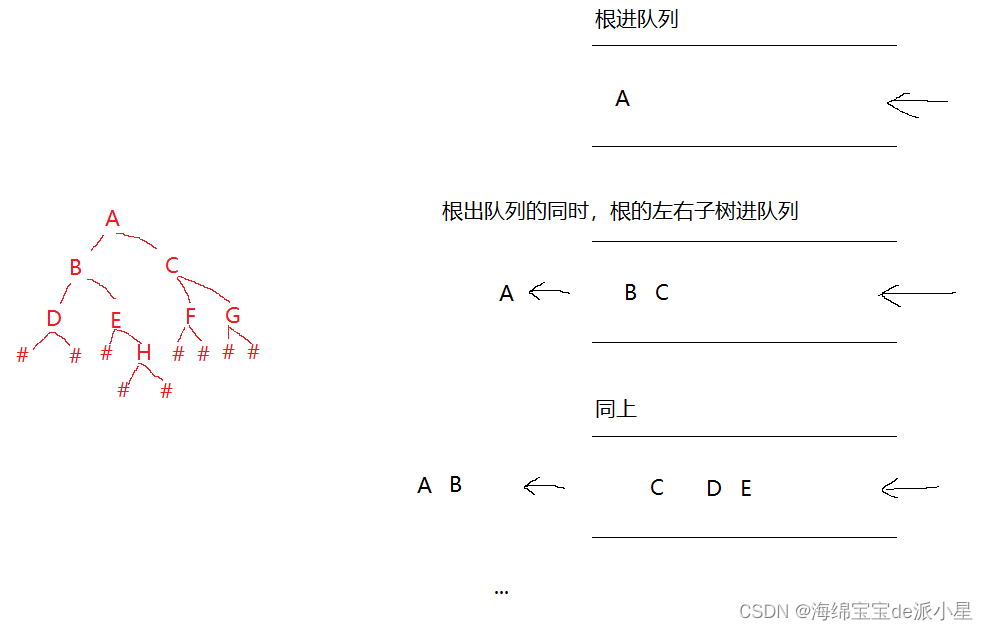
在这里插入图片描述
代码实现相较于前面来说简单一些，但需要引入队列的，关于队列的介绍：

数据结构—手撕队列栈并相互实现

下面展示要使用的队列的相关函数实现

// queue.h
typedef struct BinaryTreeNode* QDataType;typedef struct QNode
{QDataType data;struct QNode* next;
}QNode;typedef struct Queue
{QNode* phead;QNode* ptail;int size;
}Queue;// queue.c
void QueueInit(Queue* pq)
{assert(pq);pq->phead = pq->ptail = NULL;pq->size = 0;
}void QueueDestroy(Queue* pq)
{assert(pq);QNode* cur = pq->phead;while (cur){QNode* next = cur->next;free(cur);cur = next;}pq->phead = pq->ptail = NULL;pq->size = 0;
}QNode* BuyQnode(QDataType x)
{QNode* newnode = (QNode*)malloc(sizeof(QNode));if (newnode == NULL){perror("malloc fail");return NULL;}newnode->data = x;newnode->next = NULL;return newnode;
}void QueuePush(Queue* pq, QDataType x)
{assert(pq);QNode* newnode = BuyQnode(x);if (pq->ptail == NULL){assert(pq->phead == NULL);pq->phead = pq->ptail = newnode;}else{pq->ptail->next = newnode;pq->ptail = newnode;}pq->size++;
}bool QueueEmpty(Queue* pq)
{if (pq->size == 0){return true;}return false;
}void QueuePop(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));if (pq->phead->next == NULL){free(pq->phead);pq->phead = pq->ptail = NULL;}else{QNode* newhead = pq->phead->next;free(pq->phead);pq->phead = newhead;}pq->size--;
}QDataType QueueFront(Queue* pq)
{assert(pq);assert(!QueueEmpty(pq));return pq->phead->data;
}QDataType QueueBack(Queue* pq)
{assert(pq);return pq->ptail->data;
}int QueueSize(Queue* pq)
{assert(pq);return pq->size;
}

那么借助队列我们来实现刚才的层序遍历

void BinaryTreeLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);printf("%c ", front->data);QueuePop(&q);if (front->left)QueuePush(&q, front->left);if(front->right)QueuePush(&q, front->right);}printf("\n");//BinaryTreeDestory(&q);
}

二叉树的销毁

在知道了遍历的多种途径后，二叉树的销毁就很简单了，在确定代码如何实现前，先思考问题：应该选用哪种遍历来进行二叉树的销毁？

结果是很明显的，选用后序遍历是最方便的，原因在于销毁是需要进行节点的释放的，如果使用前序或者中序遍历，那么在遍历的过程中根节点会被先销毁，那么找左子树或者右子树就带来了不便(可以定义一个变量保存位置)，因此最好用后序遍历，把子树都销毁了最后销毁根

void BinaryTreeDestory(BTNode* root)
{if (root == NULL){return;}BinaryTreeDestory(root->left);BinaryTreeDestory(root->right);free(root);
}

二叉树节点个数

二叉树节点个数也是转换成子树来解决，如果为NULL就返回0，其他情况返回左右相加再加上节点本身

int BinaryTreeSize(BTNode* root)
{if (root == NULL){return 0;}return 1 + BinaryTreeSize(root->left) + BinaryTreeSize(root->right);
}

二叉树叶子节点的个数

叶子节点个数求解和上述方法相似，也是找最小的子树，但不同的地方是，叶子节点找到的条件是叶子作为根，它的左右子树都为空，符合这样的就是叶子节点，那么根据这个想法求得代码不难得到：

int BinaryTreeLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}int leftleave = BinaryTreeSize(root->left);int rightleave = BinaryTreeSize(root->right);return leftleave + rightleave;
}

二叉树查找值为x的节点

这个相对较麻烦一点，先上展开图和代码

BTNode* BinaryTreeFind(BTNode* root, BTDataType x)
{if (root == NULL){return NULL;}if (root->data == x){return root;}BTNode* ret1 = BinaryTreeFind(root->left, x);if (ret1)return ret1;BTNode* ret2 = BinaryTreeFind(root->right, x);if (ret2)return ret2;return NULL;
}

在这里插入图片描述
这里的关键动作就是判断ret1和ret2是否为空，如果是，则说明找到正确的值，那么就会一路被送出函数，相反会一直返回NULL，因此就不必担心送出其他元素的情况

二叉树是否为完全二叉树

这个思路也较为复杂，首先，需要解决的问题是用什么思路，基本思路是一个一个看，如果在某一个节点已经为空的前提下，它后面的节点还不为空，那么就说明这个不是完全二叉树

因此这个思路是不是和层序遍历很像呢？我们借助这样的思路继续写下去

当队列不为空就继续入队列出队列进行层序遍历，当遇到空就跳出，跳出循环后此时队列并不为空，继续出队列，如果发现某个元素不为空，那么就证明这并不是完全二叉树

代码实现如下：

int BinaryTreeComplete(BTNode* root)
{assert(root);Queue q;QueueInit(&q);while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front == NULL){break;}QueuePush(&q,front->left);QueuePush(&q,front->right);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front){BinaryTreeDestory(&q);return 0;}}BinaryTreeDestory(&q);return 1;
}