有意向获取代码,请转文末观看代码获取方式~也可转原文链接获取~

1 基本定义
TVFEMD+FFT+HHT组合算法是一种结合了总体变分模态分解(TVFEMD)、傅里叶变换(FFT)和希尔伯特-黄变换(HHT)的信号分解方法。这种组合算法可以实现对信号的高效分解和特征提取,并具有自适应性、鲁棒性和可解释性等优点。
首先,TVFEMD是一种基于变分模态分解的方法,可以自适应地将信号分解成多个模态函数。与传统的EMD方法相比,TVFEMD方法可以更好地处理模态交叉和模态转换问题,提高了解的精度和稳定性。
其次,FFT是一种经典的信号处理方法,可以用于提取信号中的频率成分。通过将每个模态函数进行傅里叶变换,可以得到每个模态的频谱,从而更好地理解信号的频率特性。
最后,HHT是一种非线性局部分析技术,可以用于提取信号中的瞬时特征。通过将每个模态函数进行希尔伯特-黄变换,可以得到每个模态的瞬时频率和瞬时幅度,从而更好地理解信号的时间-频率特性。
TVFEMD+FFT+HHT组合算法的优点在于:
-
具有自适应性:TVFEMD是一种自适应的信号分解方法,可以自适应地将信号分解成多个模态函数;FFT和HHT也都是自适应的变换方法,可以自适应地提取信号的特征。这种自适应性使得该组合算法可以更好地适应不同的信号类型和特征提取需求。
-
具有鲁棒性:由于TVFEMD可以抑制模态交叉和模态转换,因此可以有效地提高算法的鲁棒性。而FFT和HHT也都是经典的信号处理方法,具有较好的鲁棒性和稳定性。这种鲁棒性使得该组合算法可以更好地处理噪声干扰和异常数据。
-
具有可解释性:通过将信号分解成多个模态函数,并分别对每个模态进行傅里叶变换和希尔伯特-黄变换,可以得到每个模态的频率成分和瞬时特征,使得信号的特征更加清晰和易于理解。
需要注意的是,TVFEMD+FFT+HHT组合算法也存在一些限制和挑战。例如,FFT可能无法完全消除模态重叠和模态转换问题;而HHT则可能存在计算量大、计算速度较慢等问题。因此,在实际应用中需要根据具体问题选择合适的算法组合,并进行优化和改进。
除了以上提到的优点,TVFEMD+FFT+HHT组合算法还具有以下特点:
-
适应性更强:TVFEMD能够更好地适应不同特性的信号,包括非线性和非平稳信号。FFT和HHT也能够适应不同特性的信号,因此该组合算法能够更好地适应各种应用场景。
-
特征提取更全面:通过将信号分解成多个模态函数,并分别对每个模态进行傅里叶变换和希尔伯特-黄变换,可以得到每个模态的频率成分、瞬时特征和时间-频率特性等特征,从而更全面地提取信号的特征。
-
可扩展性更好:TVFEMD、FFT和HHT都具有较好的可扩展性,可以处理不同规模的数据。因此,该组合算法可以应用于各种规模的数据处理中。
需要注意的是,TVFEMD+FFT+HHT组合算法也存在一些限制和挑战。例如,对于一些复杂的信号,可能需要更复杂的分解方法和技术;同时,该组合算法的计算复杂度也相对较高,需要更高效的算法和计算技术来提高计算效率。
总之,TVFEMD+FFT+HHT组合算法是一种有效的信号分解和特征提取方法,具有自适应性、鲁棒性、可解释性和适应性更强等特点,可以应用于各种信号处理领域中。
另外,TVFEMD+FFT+HHT组合算法还具有以下潜在优点:
-
实时性:由于该组合算法是自适应的,因此可以实时地处理和解析信号,适用于需要实时响应的应用场景,如在线监测、控制等。
-
泛化能力强:TVFEMD、FFT和HHT都是经过大量研究和实验验证的有效方法,具有较好的泛化能力。因此,该组合算法在处理类似问题时也能够表现出较好的效果。
-
可扩展性强:随着信号处理技术的发展,新的方法和算法不断涌现。TVFEMD+FFT+HHT组合算法的可扩展性强,可以方便地加入新的方法和算法,以保持其先进性和实用性。
-
参数可调:TVFEMD、FFT和HHT都具有一些可调参数,如分解层数、滤波器类型等。这些参数可以根据具体应用场景进行调整,以优化算法的性能和结果。
然而,该组合算法也存在一些挑战和限制。例如,对于复杂信号或噪声干扰较大的信号,可能需要更精细的信号处理技术和更严格的参数调整。此外,该组合算法的计算复杂度相对较高,对于大规模数据处理可能需要较长的计算时间和较高的计算资源。
为了充分发挥TVFEMD+FFT+HHT组合算法的优势,需要针对具体应用场景进行优化和改进。这包括选择合适的分解层数、滤波器类型、参数调整等,以及结合其他信号处理技术和机器学习算法进行综合分析和预测。
2 出图效果
附出图效果如下:
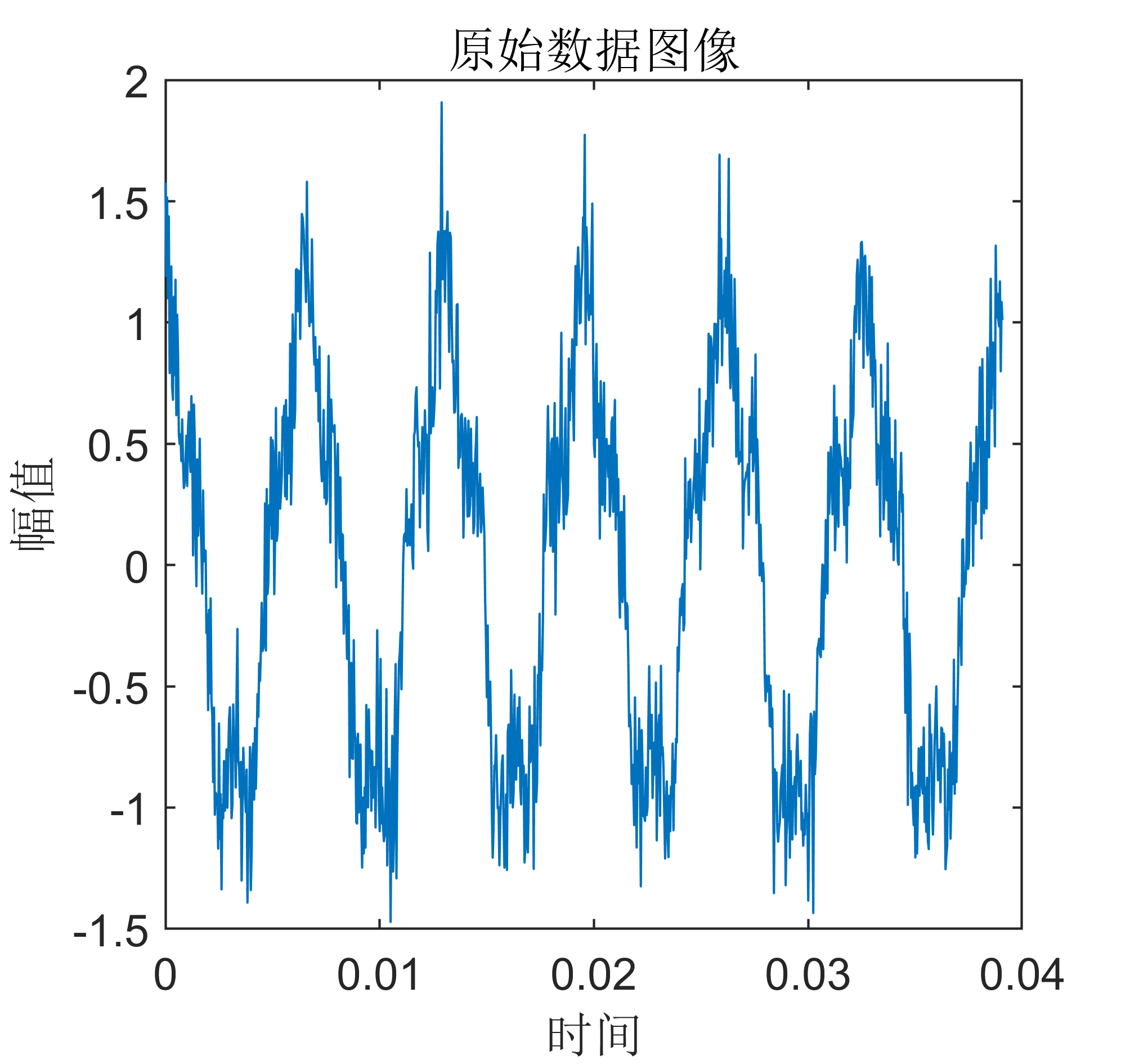


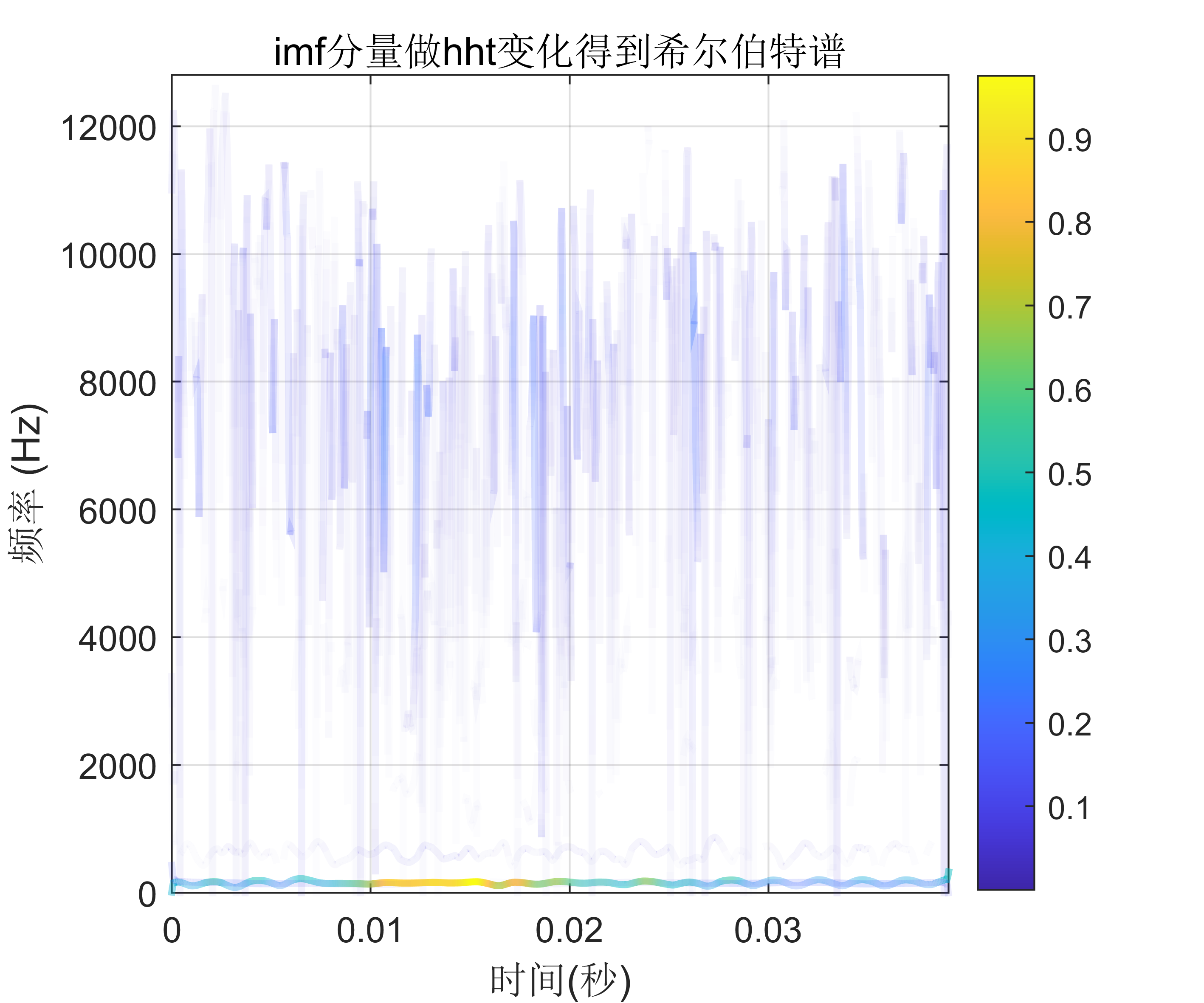
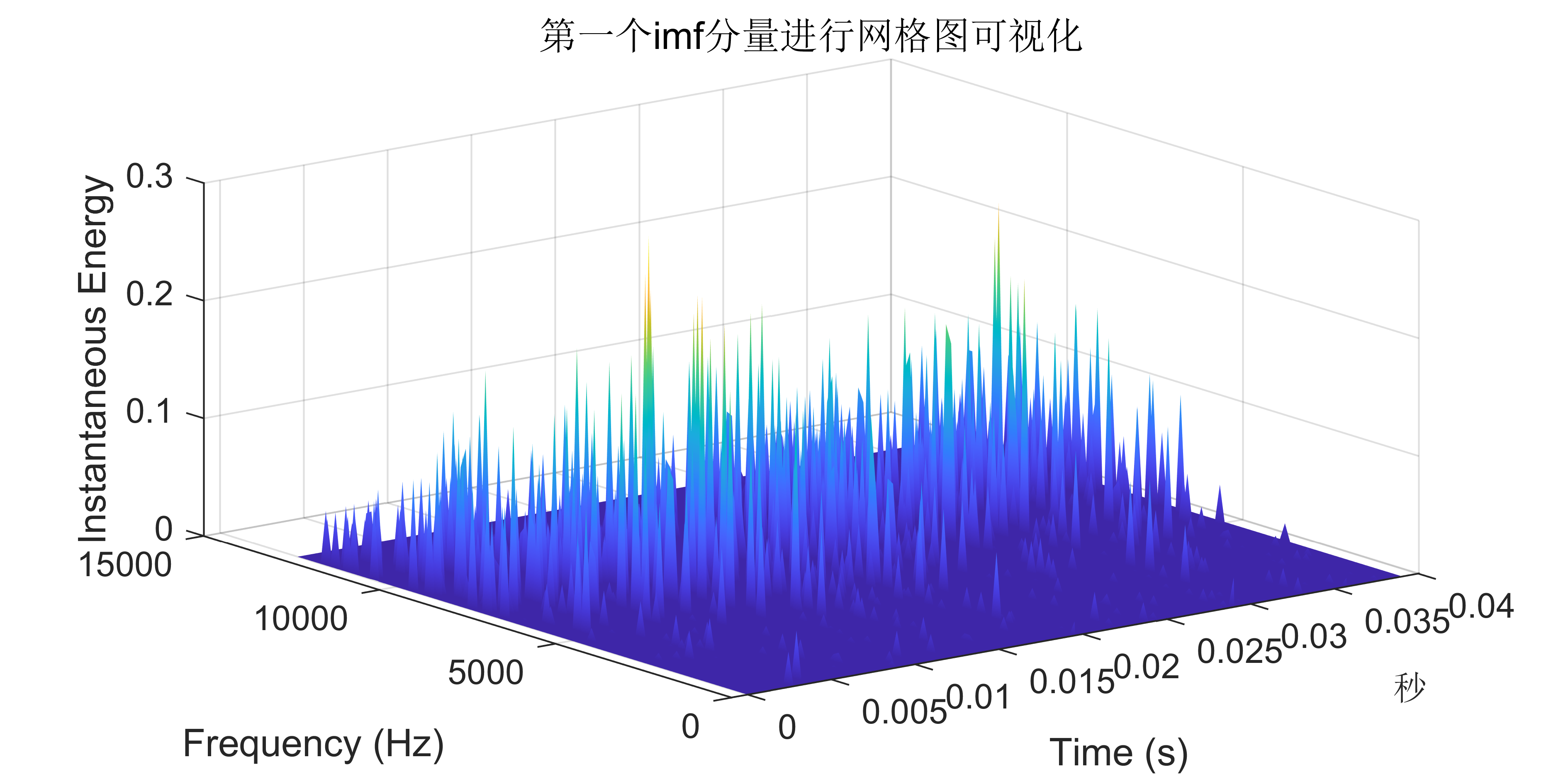
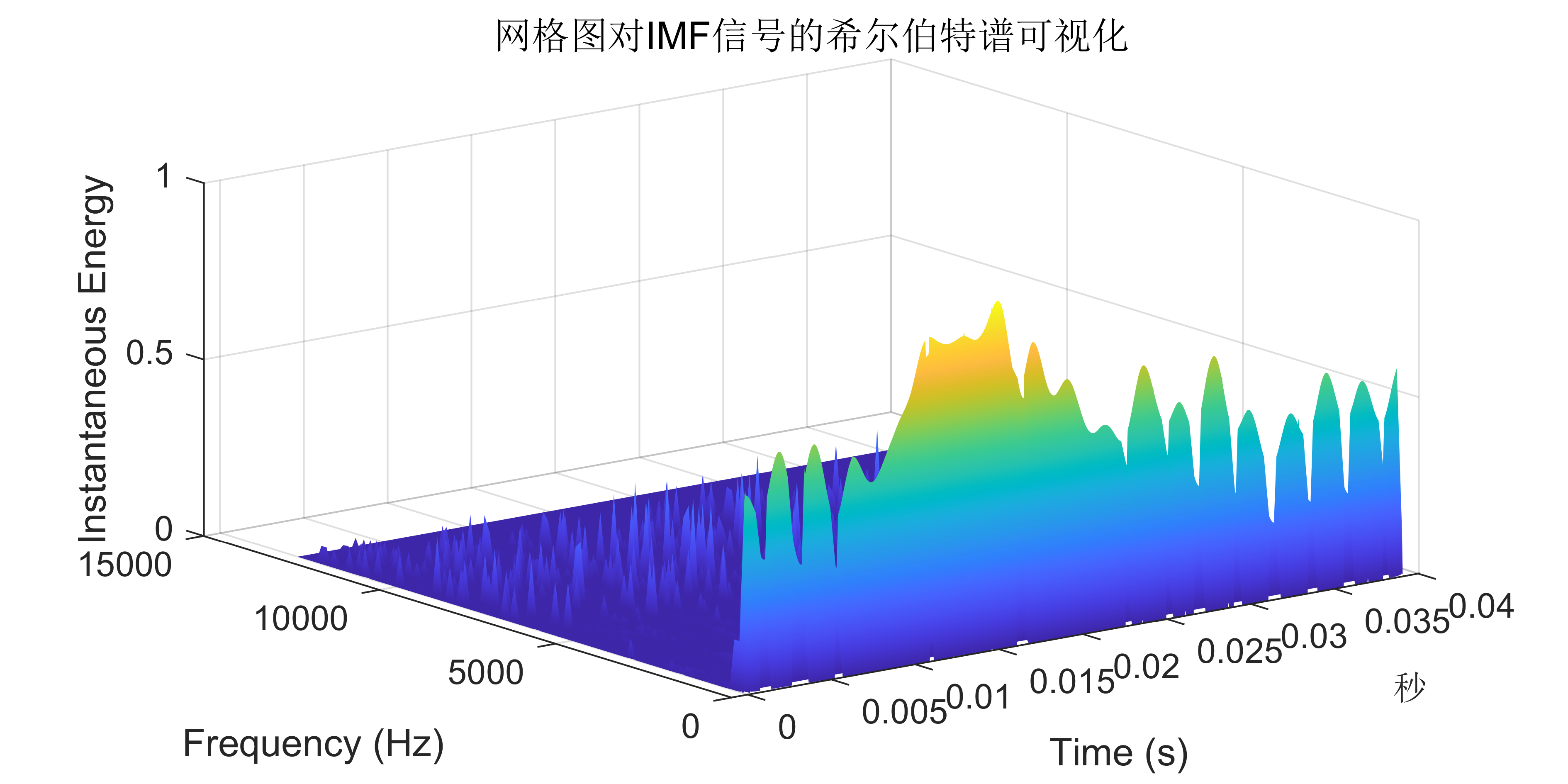
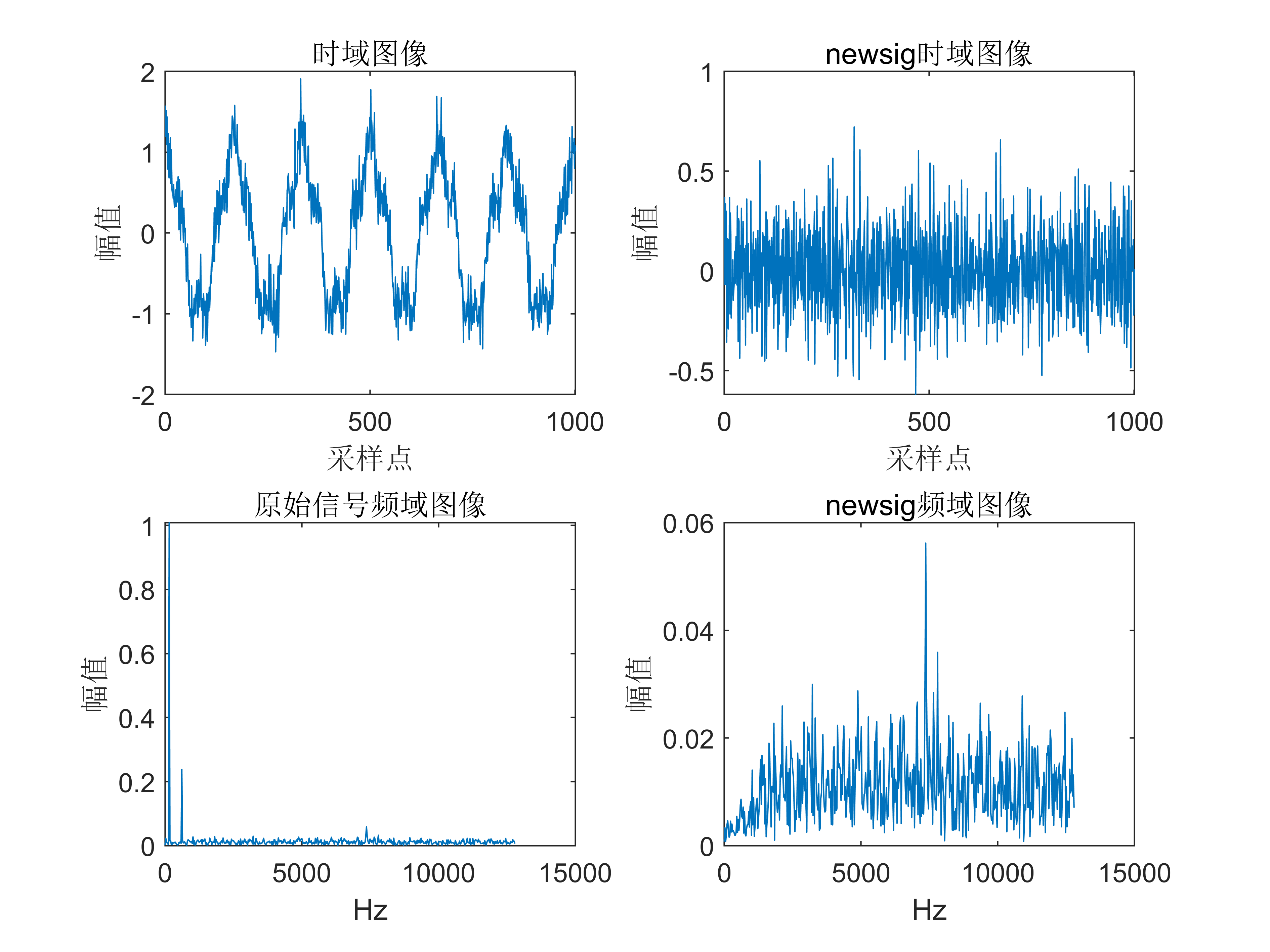
附视频教程操作:
【MATLAB】REMD信号分解+FFT+HHT组合算法