6.3.6 利用Wireshark进行协议分析(六)----网页提取过程的协议分析
利用Wireshark捕获网页访问过程中产生的应用协议报文,还原Web服务中报文的交互过程,为了防止网页直接从本地缓存中获取,我们首先需要清空浏览器保存的历史记录或者数据,具体操作步骤如下
-
清空浏览器保存历史记录:打开浏览器,清除浏览数据
如图

或者工具下的Internet选项同样也可以清空历史访问数据。
-
浏览器地址栏中填写目标主机的域名,在提取网页前浏览器会自动使用DNS域名解析服务以获得Web服务器的IP地址,所以为了捕获到域名解析协议的报文,我们还需要清空本地的DNS告诉缓存,清除所有历史解析的结果。
-
进入Doc命令界面
ipconfig /flushdns
为了验证DNS缓存已经被清空,使用命令
ipconfig /displaydns查看DNS是否被清空
-
-
运行Wireshark软件,选择网络接口开始捕获数据分组,浏览器地址栏中输入百度的网址回车,返回Wireshark停止捕获,在分组列表中包含了许多的报文,这些报文有许多与本次的访问无关,这就需要我么从中找出网页访问产生的报文。
使用Wireshark过滤功能
-
过滤出本次网页访问相关的DNS应用报文,设置过滤条件为dns是不够的,因为我们需要设置与本机相关的DNS报文。因此这里就需要用到逻辑运算符构造出较为复杂的过滤条件的表达式。IP分组的源地址或者是目标地址为主机的接口地址,如此以来过滤出的报文才是本地产生的,或者是到达本地的分组,当然报文的类型要设置为dns,那么过滤条件就为
(ip.src==192.168.184.133 || ip.dst==192.168.184.133)&&dnsip.src表示IP分组头部中的源IP地址
ip.dst表示IP分组头部中的目标IP地址
这里我们会发现分组列表面板中显示的所有报文都是DNS报文,而且这些报文是由本地产生或接收的报文,从报文的信息我们可以看到许多DNS报文与我们访问的百度Web服务器的域名解析无关
-
过滤本次网页访问过程中产生的DNS报文
还需要修改过滤条件为
(ip.src==192.168.184.133 || ip.dst==192.168.184.133)&&dns.qry.name==www.baidu.com就将关于百度的DNS的查询请求报文和DNS查询应答报文
在分组详情面板中显示了报文的封装结构,从中我们可以看出DNS的应用报文是封装在UDP数据报中进行传送的。

DNS使用的是熟知端口号53
我们查看DNS报文可以看到报文包含的详细信息。
选择应答报文查看DNS报文可以看到在answers字段中给出了解析的结果
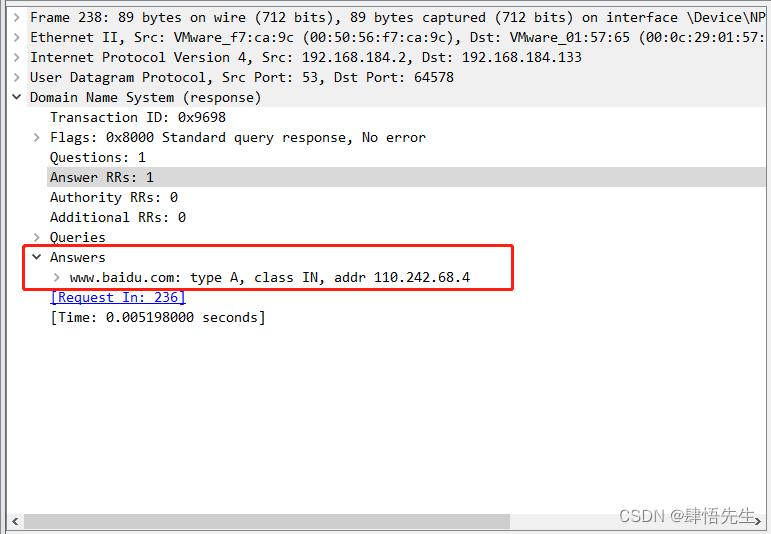
IE浏览器就可以通过这个地址提取网页。
-
分析网页提取过程中的HTTP协议的报文的交互过程,需要修改过滤条件
(ip.src==192.168.184.133 || ip.dst==192.168.184.133)&&http为了过滤出网页提取过程中的报文交互,还需要将源地址与目的地址换为百度服务器的IP地址。
(ip.src==110.242.68.4 || ip.dst==110.242.68.4)&&http报文序列显示我们可以看到浏览器程序向服务器发送了多个get命令,来提取网页中不同的资源。服务器再通过HTTP报文将所需的网页元素返回给浏览器,从HTTP报文的封装格式上,我们可以看到HTTP报文是封装在TCP分段报文中传送的。
-