题目详情：

An AVL tree is a self-balancing binary search tree. In an AVL tree, the heights of the two child subtrees of any node differ by at most one; if at any time they differ by more than one, rebalancing is done to restore this property. Figures 1-4 illustrate the rotation rules.

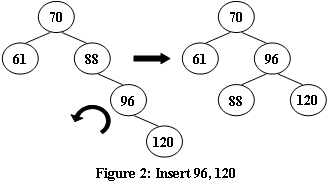
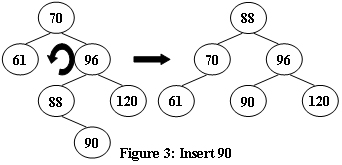
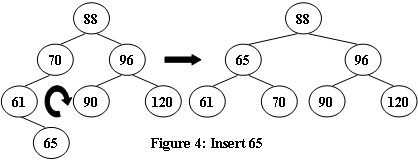
Now given a sequence of insertions, you are supposed to tell the root of the resulting AVL tree.

Input Specification:

Each input file contains one test case. For each case, the first line contains a positive integer N (≤20) which is the total number of keys to be inserted. Then N distinct integer keys are given in the next line. All the numbers in a line are separated by a space.

Output Specification:

For each test case, print the root of the resulting AVL tree in one line.

Sample Input 1:

5
88 70 61 96 120

Sample Output 1:

Sample Input 2:

7
88 70 61 96 120 90 65

Sample Output 2:

简单翻译：

就是给一个二叉平衡树的插入序列，依据这个序列构建二叉平衡树，并返回根节点

主要思路：

用插入法构建，即需要在程序里实现左右单旋与左右双旋

要特别注意的是，如果插入一个节点导致树不平衡了，我们要找到从下往上第一个不平衡的地方进行调整，调整完整个树就平衡了，而不是说要返回到最上面进行调整。

举个列子

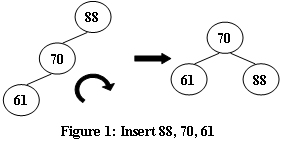
假设我们在递归的过程中，输入AVLTree是NULL，也就是如下情况：

15这里是一定平衡的（左右都是空），返回给11，11这里肯定也是平衡的，返回给9，但9就不是平衡的了

然后就可以判断让9恢复平衡应该进行哪种操作，即RR还是RL，这里判断为RR。

调整完以后，再返回到9的父节点，这个时候9的父节点再进行判断，以此类推。

第一次写错误：

（1）对树的高度的把握，准确求出树高是旋转的关键，本题实现是直接存储在树节点中，通过直接访问节点与计算左右子树高度最大值再加1求得当前节点高度

在每次旋转后都需要求出两个“交换位置”节点的各自树高

插入操作最后再求当前节点树高

（2）

左旋：根节点与左孩子“交换”位置，左孩子右子树挂到根节点左子树

右旋：根节点与右孩子“交换”位置，右孩子左子树挂到根节点右子树

左-右双旋：先根节点左孩子与它的右孩子右旋，再根节点与现在的左孩子左旋

右-左双旋：先根节点右孩子与它的左节点左旋，再根节点与现在的右孩子右旋

代码实现：

/*
定义树的数据结构，其中每个节点保存以当前节点为root的子树高度
读入数据
插入节点以建树
左旋(1)左单旋(2)左-右双旋
右旋(1)右单旋(2)右-左双旋
*/
#include <stdio.h>
#include <stdlib.h>
/*定义树的数据结构*/
typedef struct TreeNode TreeNode;
typedef TreeNode* Position;
typedef Position AVLTree;
struct TreeNode {int Data;Position Leftchild;Position Rightchild;int Height;
};
/*获取树的高度*/
int Max(int a, int b) {return a > b ? a : b;
}
int GetTreeHeight(Position root) { if(root == NULL) {return 0;}else return root->Height;
}
/*每次旋转后都要重新获取以当前节点为根节点的子树高度*/
/*左单旋*/
Position SingleLeftRotation(Position root) {Position initialRoot = root;Position newRoot = root->Leftchild;root->Leftchild = root->Leftchild->Rightchild;newRoot->Rightchild = initialRoot;newRoot->Height = Max(GetTreeHeight(newRoot->Leftchild), GetTreeHeight(newRoot->Rightchild)) + 1;initialRoot->Height = Max(GetTreeHeight(initialRoot->Leftchild), GetTreeHeight(initialRoot->Rightchild)) + 1;return newRoot;
}
/*右单旋*/
Position SingleRightRotation(Position root) {Position initialRoot = root;Position newRoot = root->Rightchild;root->Rightchild = root->Rightchild->Leftchild;newRoot->Leftchild = initialRoot;initialRoot->Height = Max(GetTreeHeight(initialRoot->Leftchild), GetTreeHeight(initialRoot->Rightchild)) + 1;newRoot->Height = Max(GetTreeHeight(newRoot->Leftchild), GetTreeHeight(newRoot->Rightchild)) + 1;return newRoot;
}
/*左-右双旋*/
Position DoubleLeftRightRotation(Position root) {root->Leftchild = SingleRightRotation(root->Leftchild);return SingleLeftRotation(root);
}
/*右-左双旋*/
Position DoubleRightLeftRotation(Position root) {root->Rightchild = SingleLeftRotation(root->Rightchild);return SingleRightRotation(root);
}
/*插入节点*/
Position Insert(Position root, int data) {if(root == NULL) {root = (Position)malloc(sizeof(TreeNode));root->Data = data;root->Leftchild = root->Rightchild = NULL;root->Height = 1;return root;}if(root->Data > data) {root->Leftchild = Insert(root->Leftchild, data);if(GetTreeHeight(root->Leftchild) - GetTreeHeight(root->Rightchild) > 1) {if(root->Leftchild->Data > data) {  //左单旋root = SingleLeftRotation(root);}else {  //左-右双旋root = DoubleLeftRightRotation(root);}}}   else if(root->Data < data) {root->Rightchild = Insert(root->Rightchild, data);if(GetTreeHeight(root->Rightchild) - GetTreeHeight(root->Leftchild) > 1) {if(root->Rightchild->Data < data) {root = SingleRightRotation(root);}else {root = DoubleRightLeftRotation(root);}}}root->Height = Max(GetTreeHeight(root->Leftchild), GetTreeHeight(root->Rightchild)) + 1;return root;
}void DeleteTree(AVLTree root) {if(root == NULL) {return;}DeleteTree(root->Leftchild);DeleteTree(root->Rightchild);free(root);return;
}/*建树*/
int BuildTree() {int N;scanf("%d", &N);AVLTree root = NULL;for(int i = 0; i < N; i++) {int data;scanf("%d", &data);root = Insert(root, data);}int ret = root->Data;DeleteTree(root);return ret;
}int main() {int root = BuildTree();printf("%d", root);return 0;
}

参考文章