目录
- 1.形式幂级数
- 2.生成函数性质
- 3.生成函数求解递推关系
- 4.生成函数在计数问题中的应用
1.形式幂级数
生成函数是解决计数问题的一种有效方法,它的中心思想是:对于一个有限或无限数列 a 0 , a 1 , a 2 , . . . {a_0,a_1,a_2,...} a0,a1,a2,...,用 { x i } ( i = 0 , 1 , . . . ) \{x^i\}(i=0,1,...) {xi}(i=0,1,...)这样的生成基构成形式幂级数 A ( x ) = a 0 + a 1 x + a 2 x 2 + . . . A(x)=a_0+a_1x+a_2x^2+... A(x)=a0+a1x+a2x2+... 使 { a i } \{a_i\} {ai} 与 { x i } \{x^i\} {xi} 成一一对应关系,由此 { a i } \{a_i\} {ai} 与 { x i } \{x^i\} {xi} 构成了一个整体,通过研究幂级数 A ( x ) A(x) A(x),导出数列 { a 0 , a 1 , a 2 , . . . } \{a_0,a_1,a_2,...\} {a0,a1,a2,...}的构造和性质。
称 A ( x ) A(x) A(x) 为序列 { a 0 , a 1 , a 2 , . . . } \{a_0,a_1,a_2,...\} {a0,a1,a2,...} 的生成函数,并记为 G ( a n ) G(a_n) G(an)
对于形式幂级数可以像收敛的幂级数那样进行运算,运算的定义和规则完全相同
定义 1.1:对于任意 A ( x ) = ∑ k = 0 ∞ a k x k A(x)=\sum^{\infty}_{k=0}a_kx^k A(x)=∑k=0∞akxk,规定 D A ( x ) DA(x) DA(x) 为 A ( x ) A(x) A(x) 的导数且 D A ( x ) ≡ ∑ k = 0 ∞ k a k x k − 1 DA(x)\equiv \sum^{\infty}_{k=0}ka_kx^{k-1} DA(x)≡∑k=0∞kakxk−1
2.生成函数性质
一个数列和它的生成函数是一一对应的。 已知数列便得知它的生成函数(系数项确定)。同理求得生成函数,则数列也随之而定。
数列 { a 0 , a 1 , a 2 , . . . } \{a_0,a_1,a_2,...\} {a0,a1,a2,...} 的生成函数为 A ( x ) = ∑ k = 0 ∞ a k x k A(x)=\sum^{\infty}_{k=0}a_kx^k A(x)=∑k=0∞akxk
数列 { b 0 , b 1 , b 2 , . . . } \{b_0,b_1,b_2,...\} {b0,b1,b2,...} 的生成函数为 B ( x ) = ∑ k = 0 ∞ b k x k B(x)=\sum^{\infty}_{k=0}b_kx^k B(x)=∑k=0∞bkxk
可以得到生成函数的如下一些性质
性质 2.1:若 b k = { 0 ( k < l ) a k − l ( k ≥ l ) b_k=\left\{\begin{matrix} 0 & (k<l)\\ a_{k-l} & (k\ge l) \end{matrix}\right. bk={0ak−l(k<l)(k≥l) 则 B ( x ) = x l ⋅ A ( x ) B(x)=x^l\cdot A(x) B(x)=xl⋅A(x)
性质 2.2:若 b k = a k + l b_k=a_{k+l} bk=ak+l ,则 B ( x ) = 1 x l ( A ( X ) − ∑ k = 0 l − 1 a k x k ) B(x)=\cfrac{1}{x^l}(A(X)-\sum_{k=0}^{l-1} a_kx^k) B(x)=xl1(A(X)−∑k=0l−1akxk)
性质 2.3:若 b k = ∑ i = 0 k a i b_k=\sum_{i=0}^{k}a_i bk=∑i=0kai,则 B ( x ) = A ( x ) 1 − x B(x)=\cfrac{A(x)}{1-x} B(x)=1−xA(x)
性质 2.4:若 b k = ∑ i = k ∞ a i b_k=\sum_{i=k}^{\infty}a_i bk=∑i=k∞ai,则 B ( x ) = A ( 1 ) − x A ( x ) 1 − x B(x)=\cfrac{A(1)-xA(x)}{1-x} B(x)=1−xA(1)−xA(x)
性质 2.5:若 b k = k a k b_k=ka_k bk=kak,则 B ( x ) = x A ( x ) B(x)=xA(x) B(x)=xA(x)
性质 2.6:若 b k = a k k + 1 b_k=\cfrac{a_k}{k+1} bk=k+1ak,则 B ( x ) = 1 x ∫ 0 x A ( t ) d t B(x)=\cfrac{1}{x}\int_{0}^{x}A(t)dt B(x)=x1∫0xA(t)dt
性质 2.7:若 c k = α a k + β b k c_k=\alpha a_k+\beta b_k ck=αak+βbk,则 C ( x ) ≡ ∑ k = 0 ∞ c k x k = α A ( x ) + β B ( x ) C(x)\equiv \sum_{k=0}^{\infty}c_kx^k=\alpha A(x)+\beta B(x) C(x)≡∑k=0∞ckxk=αA(x)+βB(x)
| 数列 | 生成函数 |
|---|---|
| {1,1,1,…} | G { 1 } = 1 1 − x G\{1\}=\cfrac{1}{1-x} G{1}=1−x1 |
| { a 0 , a 1 , a 2 , . . . } \{a^0,a^1,a^2,...\} {a0,a1,a2,...} | G { a k } = 1 1 − a x G\{a^k\}=\cfrac{1}{1-ax} G{ak}=1−ax1 |
| {0,1,2,…} | G { k } = x ( 1 − x ) 2 G\{k\}=\cfrac{x}{(1-x)^2} G{k}=(1−x)2x |
| { 0 ⋅ 1 , 1 ⋅ 2 , 2 ⋅ 3 , . . . } \{0\cdot1,1\cdot2,2\cdot3,...\} {0⋅1,1⋅2,2⋅3,...} | G { k ( k + 1 ) } = 2 x ( 1 − x ) 3 G\{k(k+1)\}=\cfrac{2x}{(1-x)^3} G{k(k+1)}=(1−x)32x |
| { 0 ⋅ 1 ⋅ 2 , 1 ⋅ 2 ⋅ 3 , 2 ⋅ 3 ⋅ 4 , . . . } \{0\cdot1\cdot2,1\cdot2\cdot3,2\cdot3\cdot4,...\} {0⋅1⋅2,1⋅2⋅3,2⋅3⋅4,...} | G { k ( k + 1 ) ( k + 2 ) } = 6 x ( 1 − x ) 4 G\{k(k+1)(k+2)\}=\cfrac{6x}{(1-x)^4} G{k(k+1)(k+2)}=(1−x)46x |
| {0,1,4,…} | G { k 2 } = x ( 1 + x ) ( 1 − x ) 3 G\{k^2\}=\cfrac{x(1+x)}{(1-x)^3} G{k2}=(1−x)3x(1+x) |
| {0,1,8,…} | G { k 3 } = x 3 + 4 x 2 + x ( 1 − x ) 4 G\{k^3\}=\cfrac{x^3+4x^2+x}{(1-x)^4} G{k3}=(1−x)4x3+4x2+x |
| { 1 0 ! , 1 1 ! , 1 2 ! , . . . } \{\cfrac{1}{0!},\cfrac{1}{1!},\cfrac{1}{2!},...\} {0!1,1!1,2!1,...} | G { 1 k ! } = e x G\{\cfrac{1}{k!}\}=e^x G{k!1}=ex |
| { ( α 0 ) , ( α 1 ) , ( α 2 ) , . . . } \{\binom{\alpha}{0},\binom{\alpha}{1},\binom{\alpha}{2},...\} {(0α),(1α),(2α),...} | G { ( α k ) } = ( 1 + x ) α G\{\binom{\alpha}{k}\}=(1+x)^\alpha G{(kα)}=(1+x)α |
| { ( n + 0 0 ) , ( n + 1 1 ) , ( n + 2 2 ) , . . . } \{\binom{n+0}{0},\binom{n+1}{1},\binom{n+2}{2},...\} {(0n+0),(1n+1),(2n+2),...} | G { ( n + k k ) } = 1 ( 1 − x ) n + 1 G\{\binom{n+k}{k}\}=\cfrac{1}{(1-x)^{n+1}} G{(kn+k)}=(1−x)n+11 |
习题1、 求序列{5, 6, 7, …, n + 5, …}的生成函数

习题2、 利用生成函数计算 1 3 + 2 3 + . . . + n 3 1^3+2^3+...+n^3 13+23+...+n3
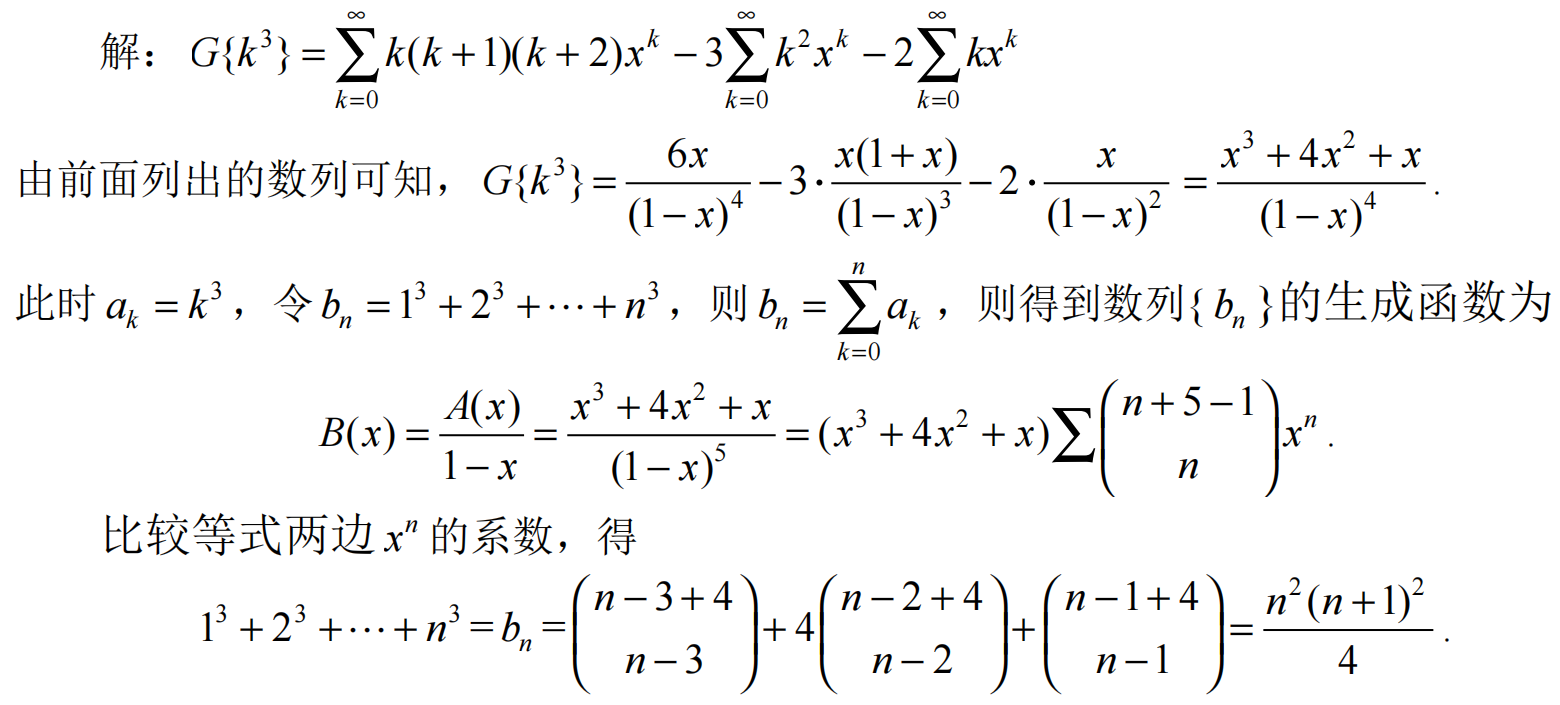
3.生成函数求解递推关系
生成函数求解递推关系基本步骤如下:
- 令 A ( x ) = ∑ n = 0 ∞ f ( n ) x n A(x)=\sum_{n=0}^{\infty}f(n)x^n A(x)=∑n=0∞f(n)xn
- 将关于 f ( n ) f(n) f(n) 的递推关系式转化成关于 A ( x ) A(x) A(x) 的方程式
- 解出 A ( x ) A(x) A(x) ,将 A ( x ) A(x) A(x) 展开成 x 的幂级数, x n x^n xn 的系数即是 f ( n ) f(n) f(n)
习题3、 用生成函数求解递推关系 { f ( n ) = 4 f ( n − 2 ) f ( 0 ) = 0 , f ( 1 ) = 1 \left\{\begin{matrix} f(n)=4f(n-2)\\ f(0)=0,f(1)=1 \end{matrix}\right. {f(n)=4f(n−2)f(0)=0,f(1)=1

习题4、 用生成函数求解递推关系 { f ( n ) = f ( n − 1 ) + 9 f ( n − 2 ) − 9 f ( n − 3 ) f ( 0 ) = 0 , f ( 1 ) = 1 , f ( 2 ) = 2 \left\{\begin{matrix} f(n)=f(n-1)+9f(n-2)-9f(n-3)\\ f(0)=0,f(1)=1,f(2)=2 \end{matrix}\right. {f(n)=f(n−1)+9f(n−2)−9f(n−3)f(0)=0,f(1)=1,f(2)=2

习题5、 用生成函数求解递推关系 { f ( n ) = f ( n − 1 ) + n 2 f ( 0 ) = 0 \left\{\begin{matrix} f(n)=f(n-1)+n^2\\ f(0)=0 \end{matrix}\right. {f(n)=f(n−1)+n2f(0)=0