108. Convert Sorted Array to Binary Search Tree
Given an integer array nums where the elements are sorted in ascending order, convert it to a
height-balanced
binary search tree.
思路:
一个高度平衡二叉树是指一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1。因为是有序数组,所以取Node的位置并不难,类似于二分法。用递归感觉比迭代更简单一点?
递归法:
class Solution(object):def traversal(self, nums, left, right):if left <= right:mid = (left + right)//2else:return None root = TreeNode(nums[mid]) # 这里采用中序遍历。想清楚递归的input和output。一开始root为Tree的根节点,逐层递归到叶节点,这时候return为None,那么叶节点是这里的root,root.left = None。再回到上一层,root为刚才叶节点的parent,root.left就是叶节点了。最后递归完毕回到root。 root.left = self.traversal(nums, left, mid-1)root.right = self.traversal(nums, mid+1, right)return rootdef sortedArrayToBST(self, nums):""":type nums: List[int]:rtype: TreeNode"""root = self.traversal(nums, 0, len(nums)-1)return root 迭代法:
from collections import dequeclass Solution:def sortedArrayToBST(self, nums: List[int]) -> TreeNode:if len(nums) == 0:return Noneroot = TreeNode(0) # 初始根节点nodeQue = deque() # 放遍历的节点leftQue = deque() # 保存左区间下标rightQue = deque() # 保存右区间下标nodeQue.append(root) # 根节点入队列leftQue.append(0) # 0为左区间下标初始位置rightQue.append(len(nums) - 1) # len(nums) - 1为右区间下标初始位置while nodeQue:curNode = nodeQue.popleft()left = leftQue.popleft()right = rightQue.popleft()mid = left + (right - left) // 2curNode.val = nums[mid] # 将mid对应的元素给中间节点if left <= mid - 1: # 处理左区间curNode.left = TreeNode(0)nodeQue.append(curNode.left)leftQue.append(left)rightQue.append(mid - 1)if right >= mid + 1: # 处理右区间curNode.right = TreeNode(0)nodeQue.append(curNode.right)leftQue.append(mid + 1)rightQue.append(right)return root
538. Convert BST to Greater Tree
Given the root of a Binary Search Tree (BST), convert it to a Greater Tree such that every key of the original BST is changed to the original key plus the sum of all keys greater than the original key in BST.
As a reminder, a binary search tree is a tree that satisfies these constraints:
- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.
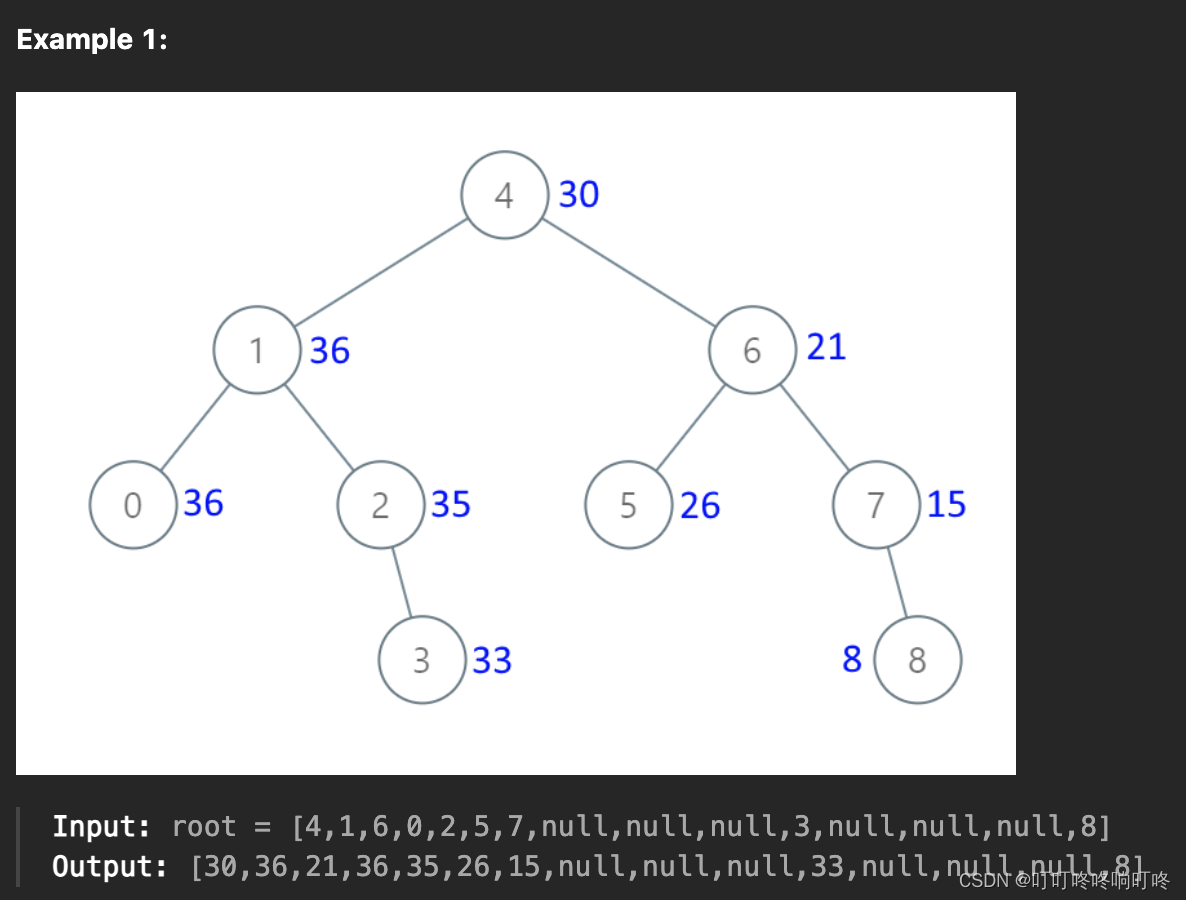
思路:二叉搜索树上每个节点按序累加之前的节点值之和,成为更大的节点值。
注意二叉树是有序的,根据例子,是进行了右中左的顺序累加的。所以也就是以右中左的顺序遍历二叉树就好。感觉把二叉树的搜索顺序搞清楚后,解题代码就比较模版化了。回头可以再好好复习一下二叉树的搜索。
递归法:
class Solution(object):def __init__(self):self.last = 0def traversal(self, root):if root is None:return self.traversal(root.right) # left root.val = root.val + self.last # middleself.last = root.valself.traversal(root.left) # right def convertBST(self, root):""":type root: TreeNode:rtype: TreeNode"""self.last = 0 self.traversal(root)return root 化简一些的递归法:
class Solution:def __init__(self):self.count = 0def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:if root == None:return '''倒序累加替换: '''# 右self.convertBST(root.right)# 中# 中节点:用当前root的值加上pre的值self.count += root.valroot.val = self.count # 左self.convertBST(root.left)return root 迭代法:
class Solution:def __init__(self):self.pre = 0 # 记录前一个节点的数值def traversal(self, root):stack = []cur = rootwhile cur or stack:if cur:stack.append(cur)cur = cur.right # 右else:cur = stack.pop() # 中cur.val += self.preself.pre = cur.valcur = cur.left # 左def convertBST(self, root):self.pre = 0self.traversal(root)return root一点碎碎念:写博客的初衷就是记录自己的练习的过程。我还处在刷题的初期->中期的阶段吧。我目前刷题的习惯是每次看一下题,有思路就直接写,没有思路就先去看一些解析。看了解析如果觉得比较清楚了就自己写出来,不然继续看答案,看了答案后盖住答案再自己写。如果看了答案还不太明白或者太绕,一次性自己肯定写不下来的话,我就会一边把答案抄一边写注释分析。这样是为了防止自己花太多时间困在一道题上(最近还真挺忙的,抽出时间来刷题),也防止畏难了就分心了。所以这个博客里的大部分答案是源于其他博客的,主要是卡哥的代码随想录(link见reference),我只是答案的搬运工,不过我附上了主要是自己写的思路。
写这个博客的目的是记录思路方便自己回看复习,也是站在一个刷题入门者的角度阐述一下自己的思路吧,如果能鼓励到其他刷题的同路人或者带来一点点的启发也算是额外之喜了。
Reference:
代码随想录