本章将详细介绍电路各个模块的设计思路和设计中需要注意的关键点,给出流水线ADC中的非理想因素,并计算出流水线ADC各个模块具体指标。根据电路中信号的传输方向,依次介绍采样保持电路、Sub_ADC,MDAC 等模块的设计。(本章有些公式推导噪声来源等问题还是需要看一看,至少得懂的子电路的各种取值和指标是怎么来的)
2.1 系统结构
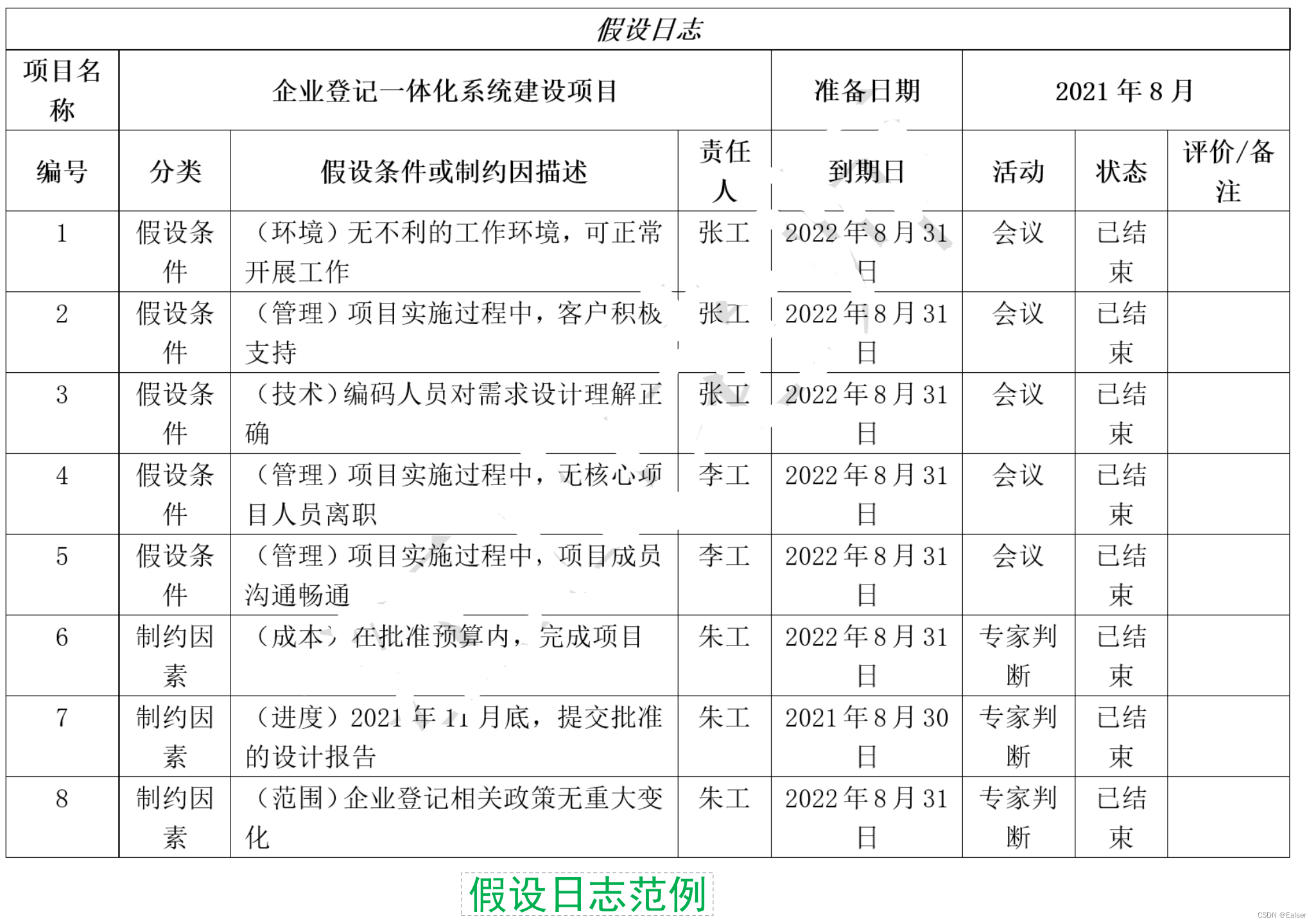
首先需要选择合适的流水线架构,即流水线级数和每一级的位数。位数越小,该级精度要求越低,对于本级的运放以及比较器的性能参数要求越低,设计上就越容易实现。但是采用低分辨率的子级整体流水线架构会包含更多的级数,整体的数字输出将需要更多的延迟时间。综合考虑,本文将选择五级 2.5 位的子级以及最后一级 2 位 Flash_ADC 结构。该结构相较于常用的 1.5 位子级的流水线结构,转换延迟时间更少。同时,如果采用 1.5 位子级,整体电路由于包含更多的运算放大器,电路整体的功耗将更高。因此为了获得更短的转换延迟时间以及更低的功耗,本文采用了 2.5 位子级的流水线结构。电路整体框图如图所示:
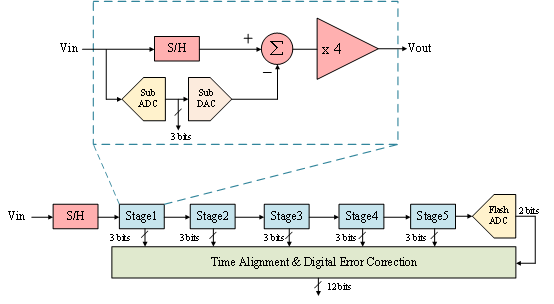
图 8 Pipeline ADC结构
2.2 非理想因素
由于流水线 ADC 是一个比较复杂的电路系统,包括很多电路模块和元器件,这些元器件和电路模块均会引入一些非理想因素,诸如开关的非线性、运放的有限增益等等,这些非理想因素都极大地制约了流水线 ADC 的性能提高,所以,在进行电路设计之前就需要预先对这些非理想因素进行考虑,把总体误差保持在一个可以容忍的范围之内。
2.2.1 MOS开关导通非线性
(这是一个老生常谈的问题,基本所有ADC的设计都会遇到这个问题。具体可以看我以前的博客)
在流水线 ADC 中,许多关键模块之中都需要用到大量的开关,所以开关性能的好坏会极大地影响流水线 ADC 的性能,其中以采样开关对性能的影响为最,所以需要对采样开关进行特殊设计。简单的理想开关采样电路和 MOS 管开关采样电路如图所示。
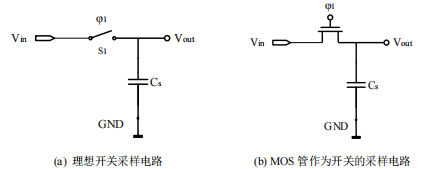
图 9 简单采样电路
图(a)是在采样理想开关的采样电路,S1 导通时,采样电容 Cs 对输入信号进行采样,S1 关断时,Cs 输出电压 Vout,若不考虑其他非理想因素,理想开关导通电阻为 0,可以无损耗的传输输入信号,而且在关断后,其等效电阻无限大,不存在漏电。但在采用如图(b)所示的 MOS 管作为开关的采样电路时,MOS 管导通电阻不可能无限小,所以其线性度会发生下降,而且关断电阻也不会无限大,还会存在漏电。当 φ1 使 MOS 管导通时,其导通电阻 Ron 为:
![]()
其中 Vthn 是 NMOS 管阈值电压,VGS 是 MOS 管栅极电压和源极电压之差,Cox 是单位面积栅氧化层电容大小,μn 是 NMOS 管载流子迁移率。在式中,前三项均为常量,在导通状态下 MOS 管栅极电压也是常数 VDD,但输入信号 Vin 是在不断变化的,而且 Vthn 也会因为衬偏效应而随输入电压产生变化,这就导致 MOS 管导通电阻 Ron 也在不断变化,MOS 管的导通电阻与采样电容 Cs 可以近似认为共同构成了一个一阶 RC 低通滤波器,其等效电路图如图所示。
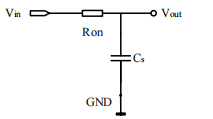
图 10 MOS开关导通时的采样电路等效图
图所示等效电路的截止频率为:
![]()
从式中可以看出,当开关为理想开关时,其导通电阻为 0,截止频率 f 为无限大,当开关采用 MOS 管开关,受限于其导通电阻,其带宽也会降低,由式还可以得出低通滤波器的传输函数为:
![]()
式(2.16)中 T 是时钟周期。推得:
![]()
从而可知,采样电路会被引入非线性。
2.2.2 开关电荷注入
MOS 开关除了非线性以外还有其他非理想因素,比较典型的是开关电荷注入和时钟馈通效应。
其中电荷注入效应只发生在 MOS 管开关断开的瞬间,这是因为 MOS 管在导通时会形成一层反型层,这层反型层存在一定量的电荷,这些电荷在 MOS 管关断以后会分别注入到 MOS 管的源漏两端,电荷注入的过程示意图如图所示,其中 Vicm 为任意直流参考电压。
电荷注入的总量即为反型层中存在的电荷量,由此可知电荷注入的电荷量为:
![]()
当 MOS 管关断时,电荷 Qch 一边注入到输入信号,这对采样不产生影响;另一边注入到采样电容 Cs 上,这就会对 Cs 采样到的电压产生影响,而且电荷注入并不是固定的每一边都注入 1/2 的电荷,这也会额外的引入非线性。
若设两边注入的电荷相等,则 Cs 上产生的电压变化大小为:
![]()
在电荷注入效应的影响下,输出信号会发生跳变,如图(b)所示。
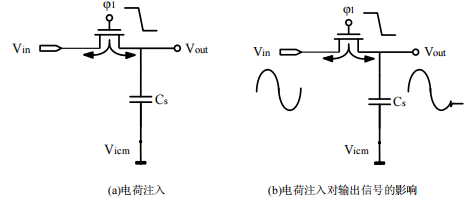
图 11 电荷注入示意图
从式中可以看出,电荷注入效应导致的误差 ΔVch 与输入电压 Vin 有关,同时 Vthn 也和 Vin 有关,所以这个 ΔVch 进一步的增加了开关的非线性。ΔVch 与采样电容成反比,在电路设计中,可以通过提高 Cs,增设虚拟管或者采用全差分的电路设计方式来降低电荷注入效应带来的误差。如今,大部分的采样电路都采用底极板采样原理,底极板采样可以很好的降低电荷注入导致的误差。
2.2.3 时钟馈通效应
时钟馈通是由于 MOS 管存在栅漏电容等寄生电容,所以开关栅极上的时钟跳变会通过这些寄生电容耦合到采样电容上,这种效应被称为时钟馈通,如图所示。
时钟馈通同样也会影响输出信号 Vout,此时的误差 ΔVck 可以表示为:
![]()
式中,Vck 是时钟高电平时的电压大小,COV是单位宽度的寄生电容,从中可以看出,时钟馈通所导致的误差在电路设计已经确定时是一个常数,不会影响采样的线性度,通常可以通过优化时序等方式来减小这个误差。
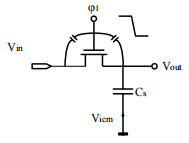
图 12 时钟馈通示意图
如图所示就是一种抵消时钟馈通效应的电路结构,在采样开关管漏级接一个虚拟 MOS 管 M2,其栅极所接时钟与采样开关反向,其尺寸是开关管的一半,这时在栅极时钟跳变时,M1和 M2 均存在时钟馈通,又 W1=2W2,则两者共同作用到采样电容 Cs 上的时钟馈通效应为:
![]()
由此可见,时钟馈通得到了完全地消除。
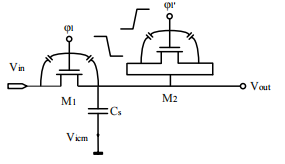
图 13 时钟馈通的一种解决方法
2.2.4 热噪声
对于一个ADC,其SNR主要由两部分构成,一是量化噪声,二是热噪声。在流水线 ADC 中,热噪声主要来源分为两部分,一部分为采样电容产生的热噪声,另外还有来自运放的热噪声。电路中的热噪声属于随机误差,无法靠全差分结构消除,在输出频谱中的底部即为热噪声。为使热噪声不会对 ADC 的精度造成影响,一般要求模数转换器总热噪声的值控制在其量化噪声之内。对于一个分辨率为 N 位的 ADC,其量化噪声可以表示为:

其中 VFS 为输出的全摆幅电压值,本设计中为 1V。可以根据热噪声的限制可以计算出采样电容的取值。
(1)采样电容的热噪声
热噪声的主要来源是流水线 ADC 中开关的导通电阻和运放,它在整个频带上呈随机分布,也是频谱中位于底部的噪声,是一种白噪声。以采样电路的热噪声为例,其功率频谱密度为:
![]()
其中 k 是玻尔兹曼常数,k=1.38´10-23J/K,T 是热力学温度,R 是采样开关总导通电阻。采样电路构成了一个低通滤波电路,设其传输函数为 H(jω),积分功率频谱密度,即为采样电路产生的热噪声电压:

从式中可以看出,实际上的热噪声只与采样电容的大小和温度有关,并与温度成正比,与电容大小成反比,所以采样电容应该尽量取大一些,但是这样也会增加面积并导致RC延时,影响电路的性能,所以电容也不能太大,还需要进行折中考量。
因为电路使全差分形式,所以电容引入的总热噪声可以表示为:
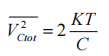
(关于采样保持电路的噪声分析,是存在不同说法的,后续有机会再补全,此处以及下文姑且先按照这样分析进行)
(2)运放的热噪声
采样保持电路的热噪声还有一部分是来自于运算放大器。,运算放大器等效输入端噪声功率谱密度为:
![]()
gm1、gmL分别为运算放大器第一级的输入管和负载管跨导,γ为沟道热噪声电流系数,约等于2/3。
在单极点系统传输函数作用下的积分,可等效成它和等效带宽的乘积,等效带宽BWn为运放闭环主极点的π⁄2倍。得到运放在保持相的输入端噪声功率为:
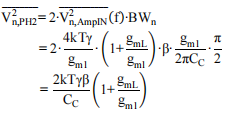
综上得到 MDAC 总体输入噪声功率:

由于运放的等效输入噪声与输入对管跨导有关,输入对管的跨导越大,其他晶体管等效到输入端的噪声越小。而流水线 ADC 中运放的增益都比较高,输入对管的跨导较大。因此当运放中其它MOS 管所贡献的热噪声等效到输入端时会有明显的衰减,所以运放的噪声系数并不是很大,其值略大于 1。设计时考虑留出裕量取噪声系数为 1.5。由于电路是全差分结构,所以总的噪声系数可以取 N=3。
故假设闭环运放系统的反馈因子为 β,等效负载电容为 CLeff,闭环工作模式下,该运放输出端噪声应为:(这是通过各种等效过后的式子,这里也都是存在不同说法的,大家看看就好,具体计算可以自己查查资料)
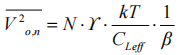
综上所述,采样保持电路的总噪声可以表示为:

等效负载电容 CLeff 包括下一子级中 MDAC 的输入电容、下一级 Sub_ADC 中所有比较器的输入电容、运放输出端共模反馈电路的电容。这里用 Cnext 表示这些电容的总合。此外,等效负载中还包括采样电容的密勒等效电容。综上,运放的等效负载电容可以表示为:
![]()
假设首级 MDAC 的采样电容与采样保持电路的 Cs 相等,其值均为 C。为便于计算,这里等效负载电容 CLeff可以取两倍的采样电容,值为 2C。则对于采样保持电路,总的噪声可以表示为:
![]()
同理,可以推导出剩余所有子级的总噪声。由于后级所采用的为 2.5 位子级,MDAC 的反馈系数为 1/4。首级 MDAC 的采样电容与采样保持电路的电容相等,其值为 C。各级 MDAC 的等效负载电容也包括下一子级的输入电容以及本级的米勒等效电容。可以表示为:
![]()
由于流水线级间增益带来的衰减,各级噪声贡献也越来越小,因此后级的采样电容值可以按照一定比例缩减,计算时按照 4 倍的比例进行电容缩减。这里取等效负载电容 CL 的值与采样电容值相等,记为 C。
则可以推导出首级 MDAC 的等效输入噪声可以表示为:

综上所述,可以推导出各级 MDAC 的总噪声。由于级间增益的缩减,各级噪声等效到首级 MDAC 输入端的总量(忽略最后一级 Flash)可以表示为:

则流水线 ADC 总的噪声功率可以表示为:

(不管是用什么方法,怎么计算的,最后等效整个ADC的噪声都大概在4~8*KT/C之间)
2.2.5 电容失配
由于工艺制造中,电容的边缘会存在一定程度的不平整,这会导致电容与标准值存在一定误差,同时寄生电容的存在也会影响电容之间的匹配。因为采样保持电路以及 MDAC 的输出精度都是依靠电容之间的匹配。以采样保持电路为例,其输出信号依赖于采样电容 CS与保持电容 CH之间的比值。
MDAC 传输函数的斜率是由电容比例决定的,故电容失配会严重影响到 MDAC 传输曲线的精确度。电容相对失配是由工艺上电容尺寸和其氧化层厚度的偏差引起的,若根据电容相对失配误差来计算所需要的电容大小,得到的电容值往往比热噪声分析得到的电容值大得多,这种面积和功耗的牺牲在 ADC 设计上并不可取,大多数 ADC 是靠数字校准技术和版图上电容的匹配来减小电容失配的影响。
分析 DAC 电容失配带来的影响需要联系 1.5bit 电容翻转型 MDAC 传输函数式,为方便计算分析,现重写如下:
![]()
排除运放有限增益的影响,简化后得到:
![]()
根据前面分析可知CS=CF,由于是相对失配,故以CF为基准,设失配下的CS,mis=CF+∆C1,代入得到:
![]()
其中ε1代表CS与CF的相对失配误差:
![]()
图表示电容失配下1.5bit MDAC 传输函数与其对应的 ADC 总体传输曲线。
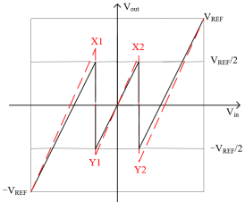
图 14 存在电容失配的MDAC传输特性曲线
其中实线表示理想情况,虚线表示了ε1大于 0 下的 MDAC 传输函数,当电容发生失配时,可以发现两个特点,第一个特点是Vin= ± VREF处,实际与理想 MDAC 传输曲线结果相同;第二个特点 MDAC 传输曲线是最大误差均发生在 D 的转换点± VREF⁄4处。推导得:
![]()
理想情况下ΔVX1_Y1为VREF,故得到理想与实际情况下ΔVX1_Y1的误差为:
![]()
根据分析,式(3-43)适用于所有量化位数的 MDAC,因为 MDAC 传输曲线转折点差值都是VREF∙(CF+∆C1)/CF的形式。误差ΔVC_mis会引起总体 ADC 传输曲线的非线性,如图所示。

图 15 电容失配下ADC的输出曲线
设 ADC 总位数为 N,本级有效量化位数为 n,令误差ΔVC_mis小于剩余级流水线量化精度的 1/2 后得到:
![]()
化简后得到:
![]()
可见首级有效量化位数越高,电容失配的影响越小。虽然电容相对失配可以通过增大电容的面积来减小,但这种方法往往会使得电容远大于热噪声约束下得到的电容值,增加了功耗和面积。所以针对采样电容和反馈电容之间相对失配,主要通过其他方法来解决。首先是在版图绘制时,注意相匹配的电容它们四周环境的一致性,使其在工艺上达到较好的匹配性;其次是采用数字算法校正电容失配带来的影响。
从电容绝对精度来看:为了降低电容失配带来的影响,一般采用精度更高 mimcap 电容,电容与标准值之间的误差与电容面积有关,可以表示为:
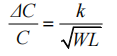
为满足 ADC 转换精度要求,由电容失配造成的误差一般要小于 1/2LSB,式中中 k 为工艺参数,WL 为电容的面积。由此可以计算出最小的电容面积,从而确定电容值。
(关于怎么确定电容精度的问题,可以查找工艺文件,会有类似下图的曲线,以及数据。要求ΔC/C < 1/2*LSB,可以根据曲线估算出大概的电容面积以及容值)

图 16 电容相对失配误差和面积的关系
2.2.6 时钟抖动
由于时钟受到电路噪声影响,其周期不是一个恒定值,会产生一个随机变化,从而导致采样产生误差,这种影响被称为时钟抖动(clock jitter)。时钟抖动包括固定抖动和随机抖动。固定抖动由信号耦合产生,随机抖动由噪声产生。时钟抖动导致采样误差是因为采样点的改变。在输入信号频率较低时时钟抖动的影响并不明显,而在输入为高频信号时采样点的改变会导致产生很大误差。时钟抖动产生误差的原理如图所示:
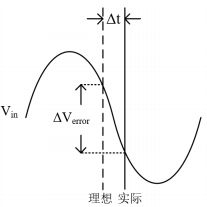
图 17 时钟抖动示意图
为采样正弦信号时发生的时钟抖动,虚线为理想采样时刻,实线为实际采样时刻,可见在∆t的采样时刻偏差下产生了∆Verror的采样电压误差,该误差随着信号频率的增大而增大。
其中正弦波信号表达式为:
![]()
误差电压为:
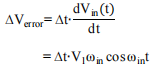
时钟抖动最差情况发生在V1为VFS/2且cos ωint为 1 的时候,将其控制在LSB⁄4以内,得到:
![]()
N 为 ADC 量化位数,VFS为满量程电平,由式得到最大允许的时钟抖动∆t,如式所示:
![]()
只考虑时钟抖动下的信噪比为:

时钟抖动会降低 ADC 的信噪比以及转换精度,并且输入信号频率越高,下降越明显。对于高速 ADC,时钟抖动的影响会更加严重。
======未完待续=======