1.树
1.1 概念
树是一种 非线性 的数据结构,它是由 n ( n>=0 )个有限结点组成一个具有层次关系的集合。 把它叫做树是因为它看 起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的 。

注意:树形结构中,子树之间不能有交集,否则就不是树形结构 !!!
一颗N结点的树有N-1条边

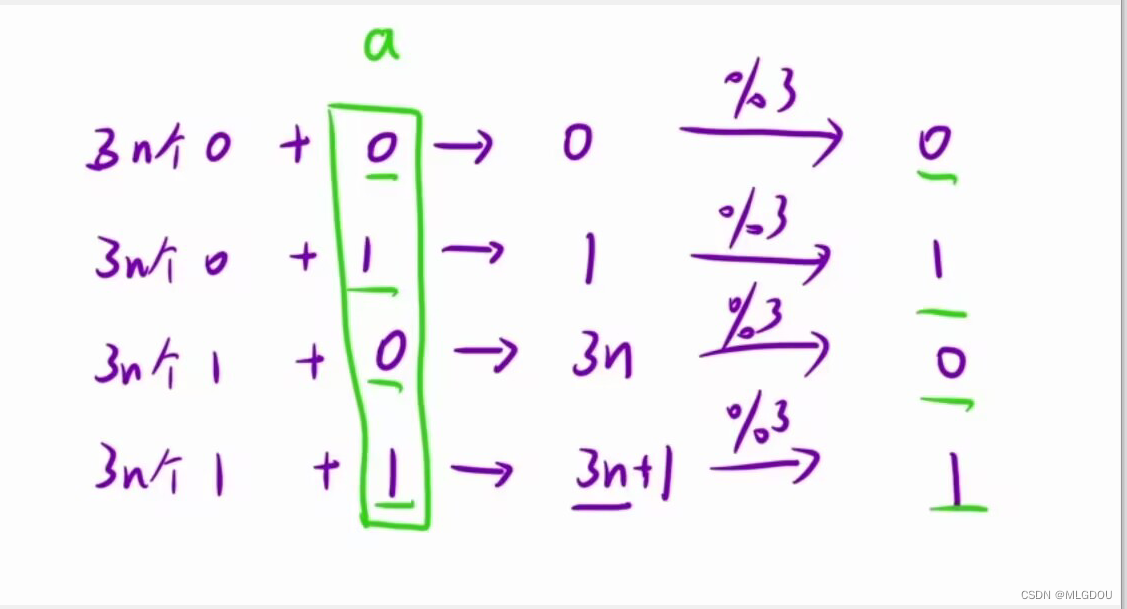
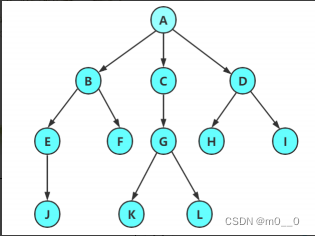
结点的度 :一个结点含有子树的个数称为该结点的度; 如上图: A 的度为 6
树的度 :一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为 6
叶子结点或终端结点 :度为 0 的结点称为叶结点; 如上图: B 、 C 、 H 、 I... 等节点为叶结点
双亲结点或父结点 :若一个结点含有子结点,则这个结点称为其子结点的父结点;如上图: A 是 B 的父结点
孩子结点或子结点 :一个结点含有的子树的根结点称为该结点的子结点;如上图: B 是 A 的孩子结点
根结点 :一棵树中,没有双亲结点的结点;如上图: A
结点的层次 :从根开始定义起,根为第 1 层,根的子结点为第 2 层,以此类推
2. 二叉树(重点)
2.1 概念
一棵二叉树是结点的一个有限集合,该集合:
1. 或者为空
2. 或者是由 一个根节 点加上两棵别称为 左子树 和 右子树 的二叉树组成

二叉树的每个节点的度 <= 2
2.2 两种特殊的二叉树
满二叉树:每层的结点数都达到最大值,就是满二叉树。(每个节点的度=2)
完全二叉树:有n 个结点的二叉树,从上到下,从左到右,编号从0至n-1的结点一 一对应时称之为完 全二叉树。
满二叉树是一种特殊的完全二叉树。

2.3 二叉树的性质
1. 若规定 根结点的层数为 1 ,则一棵 非空二叉树的第 i 层上最多有 2^(k-1) (k>0) 个结点。
2. 若规定只有 根结点的二叉树的深度为 1, 则 深度为 K 的二叉树的最大结点数是 2^k - 1 (k>=0)。
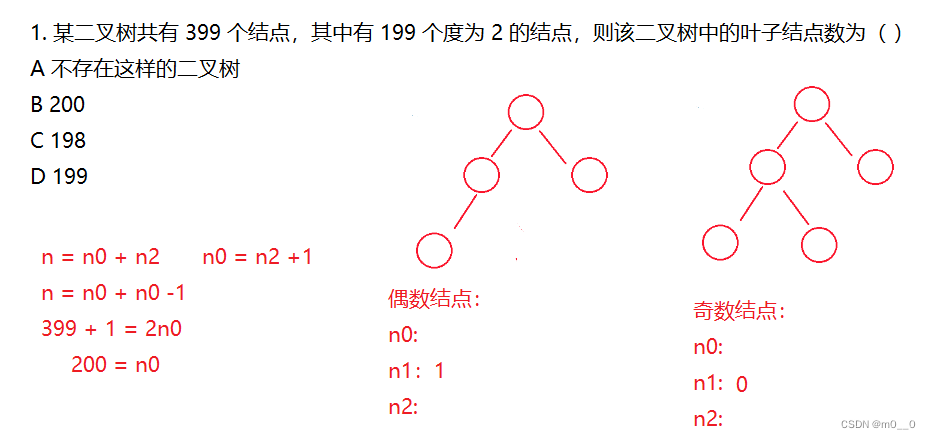
3. 对任何一棵二叉树 , 如果其 叶结点个数为 n0, 度为 2 的非叶结点个数为 n2, 则有 n0 = n2 + 1。
(结点度为0的永远比度为2的结点多1)
4. 具有 n 个结点的完全二叉树的深度 k 为log 上取整。
上取整。
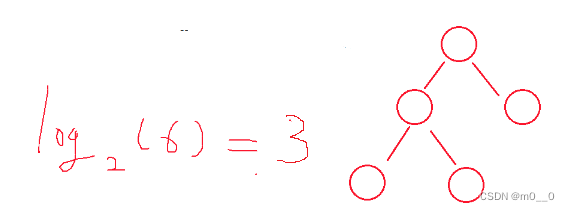
5. 对于具有 n 个结点的完全二叉树 ,如果按照 从上至下从左至右的顺序对所有节点从 0 开始编号 ,则对于 序号为 i 的结点有 :
若 i>0 , 双亲序号: (i-1)/2 ; i=0 , i 为根结点编号 ,无双亲结点
若 2i+1<n ,左孩子序号: 2i+1 ,否则无左孩子
若 2i+2<n ,右孩子序号: 2i+2 ,否则无右孩子
2.4 二叉树的遍历



前序遍历和后序遍历是无法构成一棵树的!
无法确定左、右子树
![[AutoSar]状态管理(五)Dcm与BswM、EcuM的复位实现](https://img-blog.csdnimg.cn/direct/b131bb6a2f7241ad9491fc969d7c3a43.png)