信号与线性系统翻转课堂笔记7——信号正交与傅里叶级数
The Flipped Classroom7 of Signals and Linear Systems
对应教材:《信号与线性系统分析(第五版)》高等教育出版社,吴大正著
一、要点
(1,重点)矢量和函数(信号)的正交分解,理解正交分解的特点及其实用价值;
(2)周期信号的傅里叶级数,三角傅里叶级数和指数傅里叶级数及其相互关系;
(3)周期信号的奇偶性与傅里叶级数分量之间关系。
二、问题与解答
1、结合课件中对矢量和信号正交分解特性的解释(独立性、抽取性、非冗余性、完备性),说明与非正交分解相比,对信号进行正交分解有什么好处?信号的正交分解与矢量的正交分解有什么联系和区别?
2、正交信号的概念在通信领域具有非常重要的意义。查阅相关资料,了解通信系统中各种信道复用(频分复用、时分复用、码分复用等)技术的原理,并说明在这些技术中是如何利用信号正交特性来实现信道复用的。
3、用一个区间[-∞,∞]上的不完备正交函数集,对一个周期函数f(t)进行分解。若P_0是f(t)的平均功率,P_Σ是分解所得各分量的平均功率之和,则P_0与P_Σ的大小将具有何种关系(>,<,=,≥,≤)?(分析时请参考帕斯瓦尔定理)。如果函数集是非正交的,能不能确定这样一种关系?为什么?
4、用一个或者多个函数的加权和来近似表达任意的函数f(t),这既可以理解为对f(t)的一种分解,也是数学中的一个逼近问题。其中最关键的就是确定合适的加权系数,以使得加权和与f(t)最为接近,即最佳(最优)逼近。对于何为“最佳”的逼近,需要有一个评价标准,称为“最优准则”。其中,最小均方误差准则(教材式4.1-7)是最常用的一种最优准则,除此之外,也还有很多其他的最优准则。试讨论:①如果采用不同于式4.1-7的最优准则,所得到的最佳加权系数会不会有所不同?②最大误差最小化准则,是另一种比较常用的最优准则,请查阅相关资料,比较该准则与最小均方误差准则的区别,并结合不同的应用背景,讨论这两种准则各自适用的场景。
5、基于教材式(4.1-9),推导求傅里叶系数的公式(4.2-3)、(4.2-4)和求复傅里叶系数的公式(4.2-20),总结两种傅里叶系数之间的关系,比较傅里叶系数和复傅里叶系数的自变量取值范围有何不同。
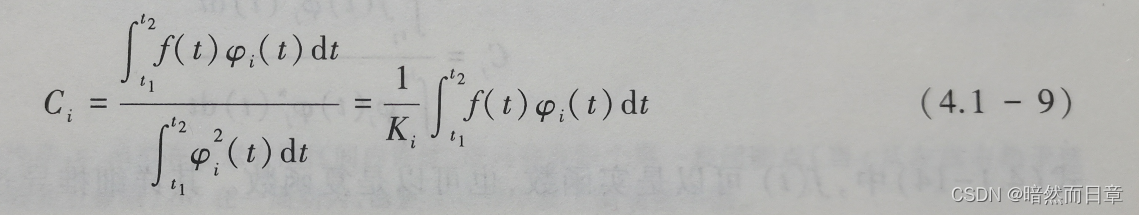

6、基于课后习题4.10,讨论信号的奇偶性与其所含谐波分量的特点。

1、信号的正交分解
结合课件中对矢量和信号正交分解特性的解释(独立性、抽取性、非冗余性、完备性),说明与非正交分解相比,对信号进行正交分解有什么好处?信号的正交分解与矢量的正交分解有什么联系和区别?
独立性:每一个正交基底可以视为具有某种独立属性的基本矢量,而这种属性在其它任意基底上都不具备。
抽取性:求任意矢量与该正交基的内积(正交投影),就可以把矢量中与该正交基底具有相同特性的分量全部抽取出来。
非冗余性:投影到某个正交基底的分量不包含可以投影到其它任意基底的部分(在其它任意基底的投影为0),而只能被它所对应的正交基底所唯一地抽取。
完备性:一个N维矢量在N维空间正交分解后的各分量的总和包含了该矢量的所有信息。
好处:对信号的正交分解是以某个区间内的完备正交函数集作为基底,可以把定义在该区间的任意函数(信号)分解为多个正交分量之和,且分解后的信号能够保留原信号的所有信息,抽取的分量具有相互独立性。
联系:一个连续信号相当于一个无穷维的矢量、分解后的各分量总和都包含了其全部信息,信号分解是函数分解的一种特例。概念相似,由矢量分解可以推广到信号的正交分解。
区别:信号的正交分解用一组完备正交函数集来表示,子函数表示各分量,而矢量正交分解是正交基底表示各分量。抽取性中矢量正交分解中任意矢量与该正交基得到内积,可以把矢量中与该正交基底具有相同特征的分量全部抽取出来,而信号正交分解中的抽取性可以该函数中具有不同属性的分量分别抽取出来,矢量正交分解是分解成垂直的向量,信号的正交分解是分解成几个正交函数。
2、信号正交与信道复用
正交信号的概念在通信领域具有非常重要的意义。查阅相关资料,了解通信系统中各种信道复用(频分复用、时分复用、码分复用等)技术的原理,并说明在这些技术中是如何利用信号正交特性来实现信道复用的。
频分复用:按照频率的不同来复用多路信号的方法。在频分复用中,信道的带宽被分为若干个相互不重叠的频段,每路信号占用其中一个频段,因而在接受端可以采用适当的带通滤波器将多路信号分开,从而恢复出所需要的信号。
根据信号正交分解特性的独立性、抽取性、非冗余性把不同频率的信号进行分解。
时分复用:利用各信号的抽样值在时间上不相互重叠,来达到在同一信道中传输多路信号的一种方法。时分多路复用以时间作为信号进行正交分割,使各路信号在时间轴上互不重叠。
根据信号正交分解特性独立性、抽取性、非冗余性把时间信号进行分解。
码分复用:用一组包含互相正交的码字的码组携带多路信号。根据信号的正交特性把码字分为相互正交的码组。
根据信号正交分解特性独立性、抽取性、非冗余性把码字信号进行分解。
3、函数正交性&信号分解中功率分析
用一个区间[-∞,∞]上的不完备正交函数集,对一个周期函数f(t)进行分解。若P_0是f(t)的平均功率,P_Σ是分解所得各分量的平均功率之和,则P_0与P_Σ的大小将具有何种关系(>,<,=,≥,≤)?(分析时请参考帕斯瓦尔定理)。如果函数集是非正交的,能不能确定这样一种关系?为什么?
帕斯瓦尔(Parseval)定理:对于完备正交函数集,正交分解前后能量守恒。

4、信号正交分解与最优准则
用一个或者多个函数的加权和来近似表达任意的函数f(t),这既可以理解为对f(t)的一种分解,也是数学中的一个逼近问题。其中最关键的就是确定合适的加权系数,以使得加权和与f(t)最为接近,即最佳(最优)逼近。对于何为“最佳”的逼近,需要有一个评价标准,称为“最优准则”。其中,最小均方误差准则(教材式4.1-7)是最常用的一种最优准则,除此之外,也还有很多其他的最优准则。试讨论:①如果采用不同于式4.1-7的最优准则,所得到的最佳加权系数会不会有所不同?②最大误差最小化准则,是另一种比较常用的最优准则,请查阅相关资料,比较该准则与最小均方误差准则的区别,并结合不同的应用背景,讨论这两种准则各自适用的场景。

(1)不会,因为正交基底之间是具有独立性的,每一个正交基底可以视为具有某种独立属性的基本矢量,而这种属性在其它任意基底上都不具备,所以找到最佳加权系数一定相同。
(2)
最小均方误差准则:选择一组时域采样值,采用最小均方误差算法,以使均方误差最小,这一方法注重的是在整个频率区间内,总误差全局最小,但不能保证局部频率点的性能,有些频点可能会有较大的误差。(适合对于整体误差考虑多,不追究各别点的误差的情况)
最大误差最小化准则:通过不同频率范围内实现不同的加权函数,实现在不同频段的加权误差最大值相同,从而实现在最大误差在满足要求的条件下达到最小值(适合点与点之间进行运算,注重波形的情况)。
5、傅里叶系数&复傅里叶系数的推导
基于教材式(4.1-9),推导求傅里叶系数的公式(4.2-3)、(4.2-4)和求复傅里叶系数的公式(4.2-20),总结两种傅里叶系数之间的关系,比较傅里叶系数和复傅里叶系数的自变量取值范围有何不同。
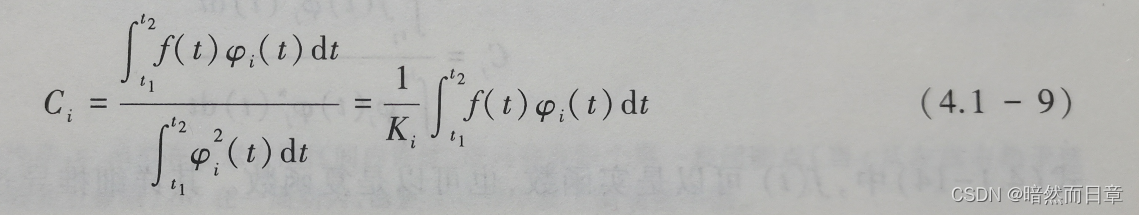
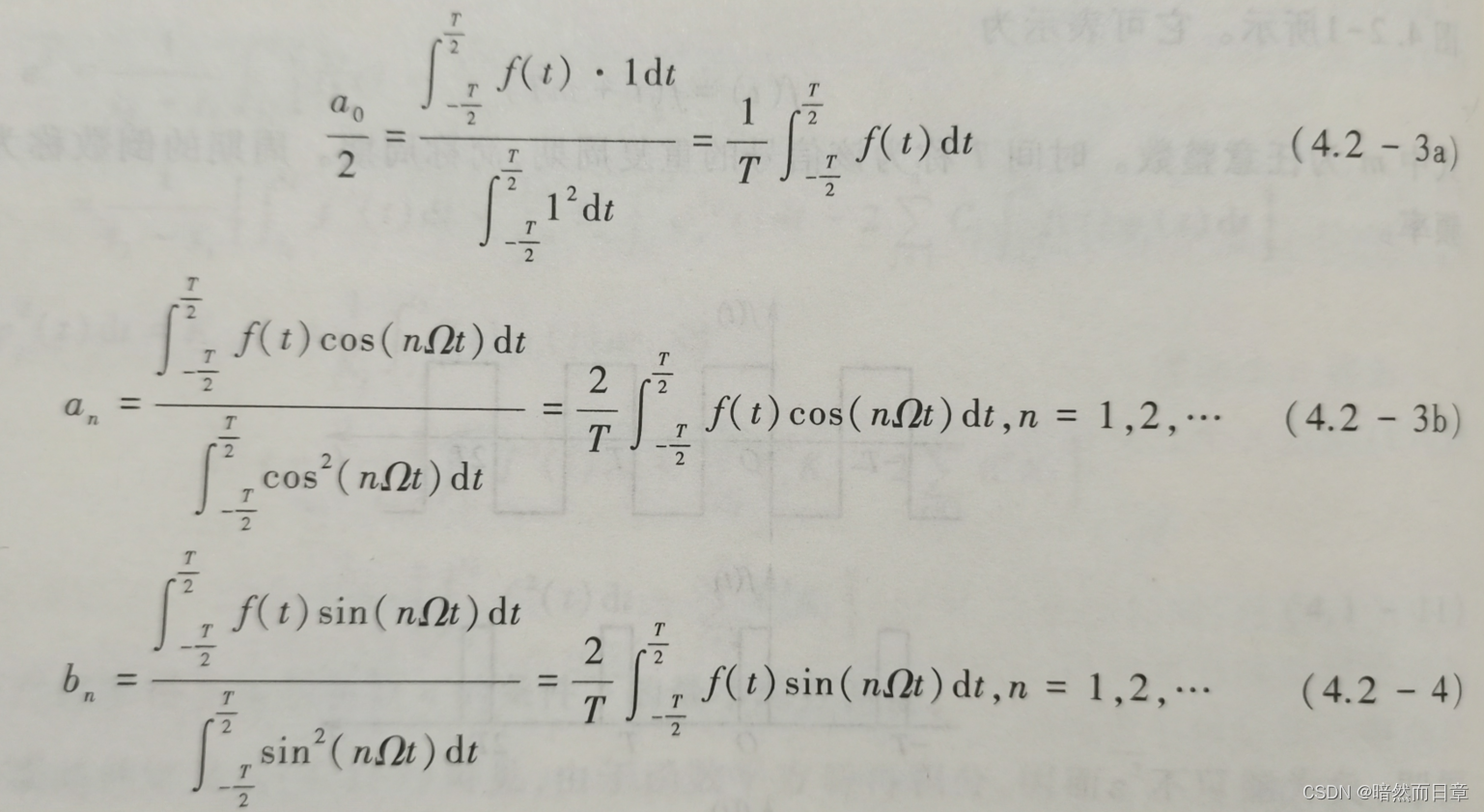


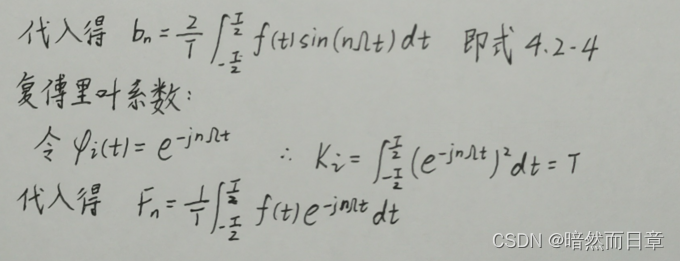


傅里叶系数的自变量取值范围:[0,+∞)
复傅里叶系数的自变量取值范围:(-∞,+∞)
6、
基于课后习题4.10,讨论信号的奇偶性与其所含谐波分量的特点。
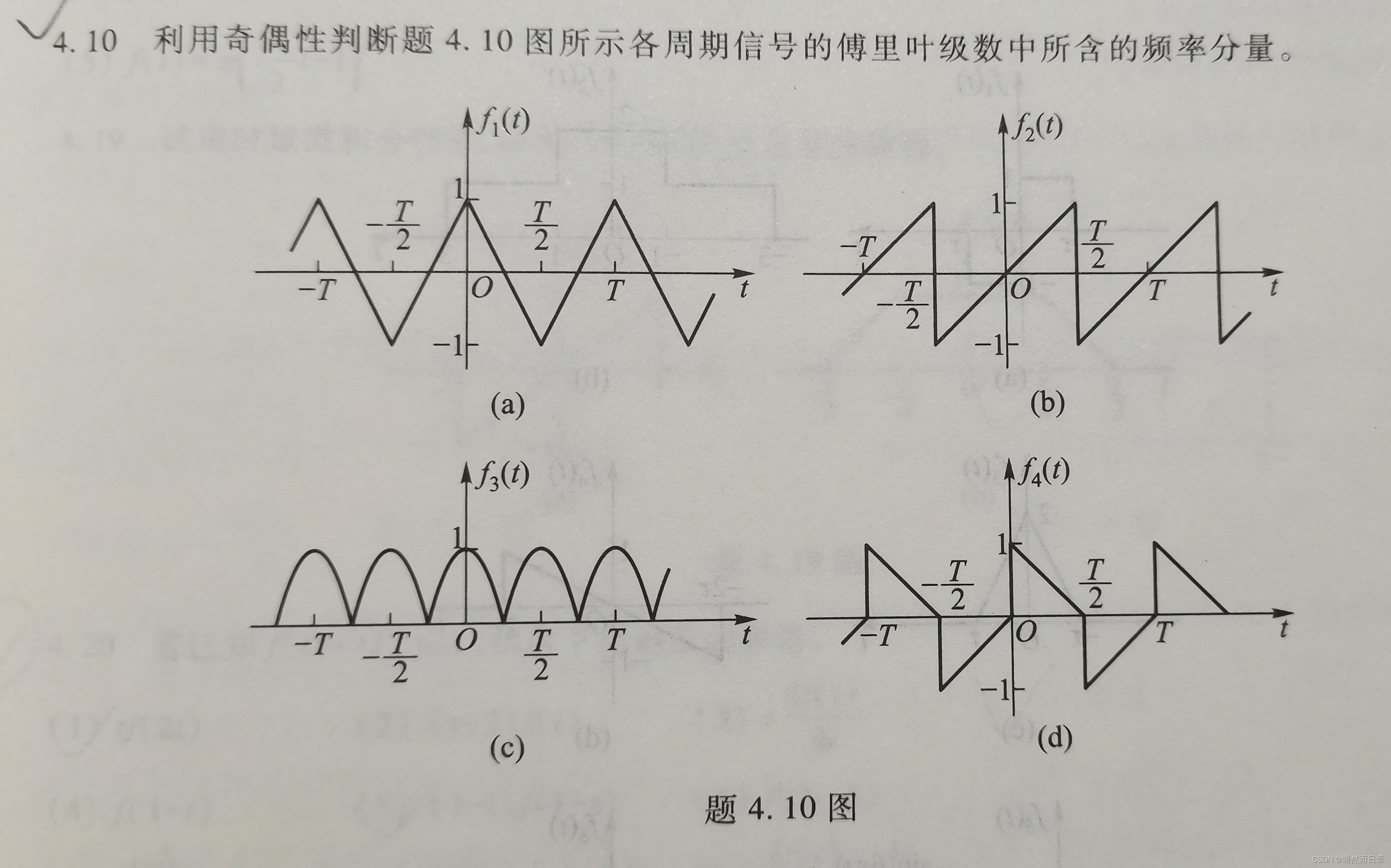


特点:
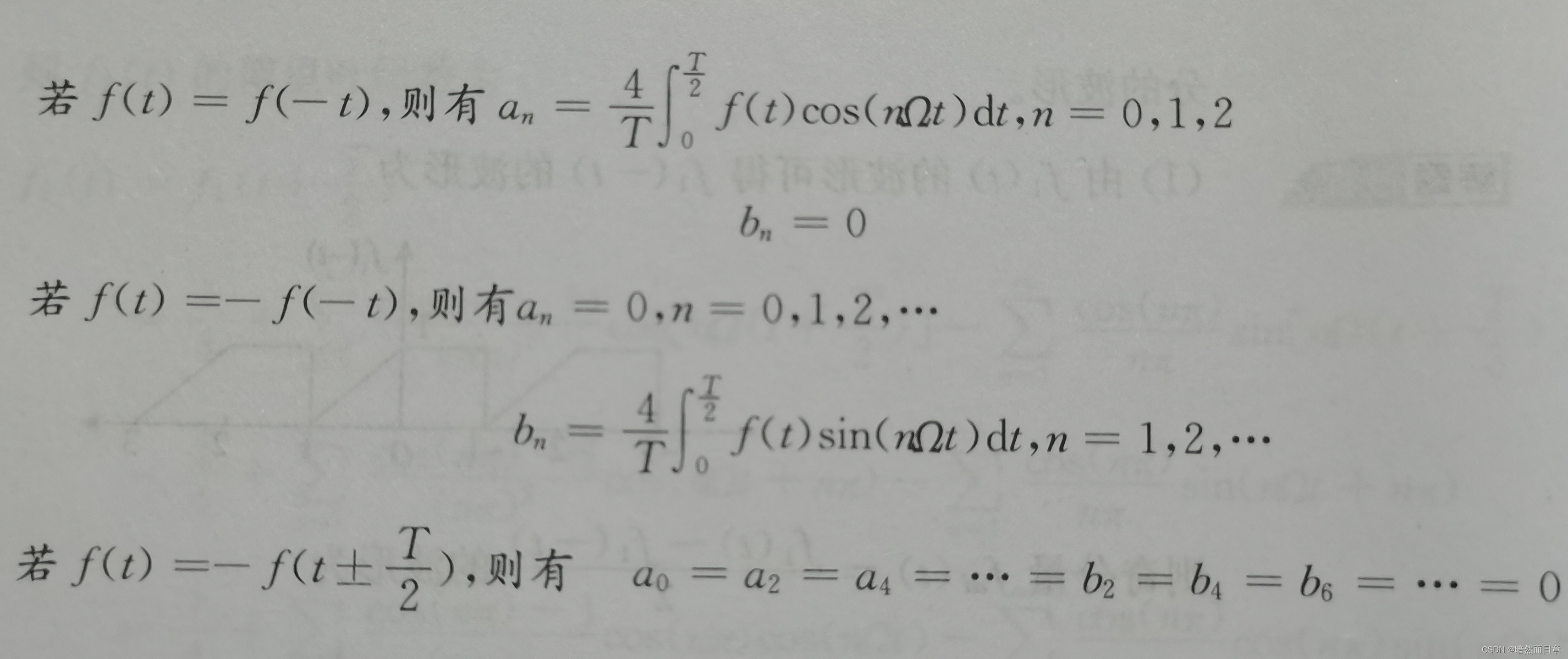
三、反思总结
暂无