信号与线性系统翻转课堂笔记10——傅里叶变换的性质

信号与线性系统翻转课堂笔记10——傅里叶变换的性质

The Flipped Classroom10 of Signals and Linear Systems

对应教材：《信号与线性系统分析（第五版）》高等教育出版社，吴大正著

一、要点

（1，重点）熟练掌握傅里叶变换的各种性质，能利用性质来求傅里叶变换，了解各种性质的物理含义及其应用价值；
（2）了解信号能量谱和功率谱的概念；
（3）掌握采用MATLAB的符号运算和数值运算的方式来求信号的傅里叶变换；
（4）初步了解线性相位、幅度调制（频谱搬移）、频谱分析中的测不准原理等与实际应用密切相关的概念。

二、问题与解答

1、将非周期信号f(t)在时域进行平移得到f(t-t_0 )。与f(t)的频谱相比，f(t-t_0 )的幅度和相位频谱分别会发生何种变化？设f(t)为宽度为2、幅度为1的 矩形脉冲信号（参见教材图4.5-3(a)），用MATLAB的符号运算方式（fourier函数），分别求f(t)和f(t-0.2)的傅里叶变换并分别画出它们的幅度和相位频谱，对比分析两者的异同。讨论：为什么说f(t-0.2)的相位频谱是一种“线性相位”？如何从时域的角度理解线性相位的含义？如果改变平移量t_0的大小，会对相位频谱产生什么影响？请用MATLAB画出两种不同 对应的相位频谱并总结分析。

2、采用MATLAB数值计算的方式，重新计算上一题中f(t)和f(t-0.2)的幅度和相位频谱，与符号计算的结果进行比较，并请解释计算程序的基本原理。傅里叶变换的数值计算方法和程序，已经在预备训练三中提出了要求。未能完成预备训练三所布置任务的同学（已经完成的同学，请采用自己的数值计算程序），可参考以下所给出程序。请读懂该程序原理，并根据信号f(t)的不同，设置适当的信号取样间隔T、信号截取范围和频谱分析范围。
数值计算参考程序：

T=0.08;                                     % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+0.8)-heaviside(t-1.2);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
subplot(2,1,1)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(2,1,2)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');

3、设f(t)为第1题的矩形脉冲，选用一个具有适当频率的余弦信号cos⁡(ω_c t)（请参考课件第98页例4-5-6），用MATLAB画出f(t)cos⁡(ω_c t)的频谱（幅度谱和相位谱合二为一，可自行选择符号计算和数值计算方式，若采用数值计算，需对第2题给出的参考程序略作修改）。结合课件例4-5-6，讨论“频谱搬移”（幅度调制）的概念及其实现方法。f(t)cos⁡(ω_c t)其实也可以视为f(t)和cos⁡(ω_c t)在时域相乘，根据频域卷积定理（教材式4.5-28）也能得到相同的结论，请基于频域卷积定理推导f(t)cos⁡(ω_c t)的傅里叶变换（参见课件第123页例4-6-0）。

4、从时域的角度来看，对上一题的f(t)cos⁡(ω_c t)还有另外一种解释：它是利用门函数截取了余弦信号cos⁡(ω_c t)的一段样本。而对这段样本进行傅里叶变换，所得到的频谱上题所示。但是，由周期信号的傅里叶变换可知，cos⁡(ω_c t)的理论频谱应该如教材图4.7-1(a)中所示的两个频域冲激。也就是说，如果只截取cos⁡(ω_c t)的一段样本，来计算cos⁡(ω_c t)的频谱，其结果是不准确的！这种不准确性也称为“测不准原理”，它反映了采用观测的方法来分析信号的频谱所面临的局限性。试分析讨论：①比较上一题求得的f(t)cos⁡(ω_c t)频谱与cos⁡(ω_c t)理论频谱之间的区别与联系。②通过改变矩形脉冲的宽度，截取不同长度的cos⁡(ω_c t)样本，用MATLAB分别分析其频谱，比较不同长度样本频谱的差异，分析若想改善频谱分析的准确性，应该如何选取样本长度？

5、分别针对前面各题的矩形脉冲f(t)、余弦信号cos⁡(ω_c t)以及f(t)cos⁡(ω_c t)，分别进行时域尺度变换（变换系数自定），采用MATLAB符号或者数值计算，求尺度变换后的频谱。根据结果总结时域尺度变换对频谱的影响，并讨论这一结论对于确定通信系统的带宽有何意义？

6、什么是傅里叶变换的对称性质？利用该性质，求解习题4.17。若用门函数g_τ (⋅)来表示幅度为1、宽度为τ的对称矩形脉冲，则g_2 (t)的傅里叶变换是什么？g_2 (jω)的傅里叶反变换是什么？

7、分别利用傅里叶变换的微分性质和时域卷积定理，求图示对称三角形脉冲的傅里叶变换（理论计算），并用MATLAB画出其频谱（幅度相位谱合二为一）。（提示：三角形脉冲可以表示为两个宽度相同的矩形脉冲的卷积）
在这里插入图片描述

1、时域平移对频谱（傅里叶变换）的影响

将非周期信号f(t)在时域进行平移得到f(t-t_0 )。与f(t)的频谱相比，f(t-t_0 )的幅度和相位频谱分别会发生何种变化？设f(t)为宽度为2、幅度为1的矩形脉冲信号（参见教材图4.5-3(a)），用MATLAB的符号运算方式（fourier函数），分别求f(t)和f(t-0.2)的傅里叶变换并分别画出它们的幅度和相位频谱，对比分析两者的异同。（第一问）讨论：为什么说f(t-0.2)的相位频谱是一种“线性相位”？如何从时域的角度理解线性相位的含义？（第二问）如果改变平移量t_0的大小，会对相位频谱产生什么影响？请用MATLAB画出两种不同 对应的相位频谱并总结分析。（第三问）

（1）
幅度谱不变，相位谱变化。

syms t w
f(t)=heaviside(t+1)-heaviside(t-1);
Fjw=fourier(f(t));
fai=log(Fjw/abs(Fjw))/j;
subplot(3,2,1)
fplot(t,f(t));set(gca,'XTick',-5:5);
xlabel('t');ylabel('f(t)'); title('矩形脉冲信号')
subplot(3,2,3)
fplot(w/2/pi,abs(Fjw),[-20,20]);
xlabel('f(Hz)');ylabel('幅度'); title('矩形脉冲信号的幅度谱')
subplot(3,2,5)
fplot(w/2/pi,angle(Fjw)/pi*180,[-30,30]);
xlabel('f(Hz)');ylabel('相角'); title('矩形脉冲信号的相位谱')syms t w
f(t)=heaviside(t-0.2+1)-heaviside(t-0.2-1);		%右移0.2
Fjw=fourier(f(t));
fai=log(Fjw/abs(Fjw))/j;
subplot(3,2,2)
fplot(t,f(t));set(gca,'XTick',-5:5);
xlabel('t');ylabel('f(t-0.2)'); title('右移0.2后的矩形脉冲信号')
subplot(3,2,4)
fplot(w/2/pi,abs(Fjw),[-20,20]);
xlabel('f(Hz)');ylabel('幅度'); title('矩形脉冲信号的幅度谱（右移后）')
subplot(3,2,6)
fplot(w/2/pi,angle(Fjw)/pi*180,[-30,30]);
xlabel('f(Hz)');ylabel('相角'); title('矩形脉冲信号的相位谱（右移后）')

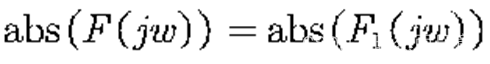
在这里插入图片描述
幅度频谱不变：
在这里插入图片描述
相位谱作了延时，向下移动：
在这里插入图片描述
（2）
线性相位特性的时域解释：假设一个信号f(t)可以看作是由两个信号f1(t)和f2(t)组成的，其中信号f1(t)的频率为0.5Hz,信号f2(t)的频率为1Hz,即信号f2(t)的频率为信号f1(t)频率的两倍。当我们把这个信号在时域上向右(或向左)平移t0=0.5s时，对于信号f1来说，其相位会变化90度，而信号f2的相位则会变化180度。
结论：同等时移t0,不同频率信号的相位变化量与频率成正比。
（3）
线性系数不一样，斜率改变。
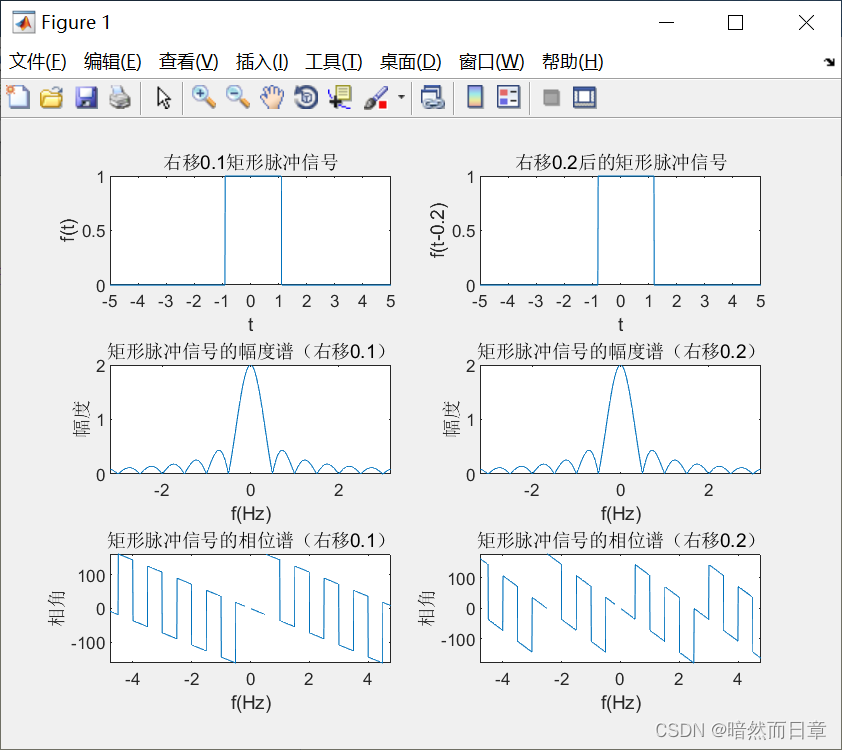
在这里插入图片描述

2、数值计算方法求频谱（傅里叶变换）

采用MATLAB数值计算的方式，重新计算上一题中f(t)和f(t-0.2)的幅度和相位频谱，与符号计算的结果进行比较，并请解释计算程序的基本原理。傅里叶变换的数值计算方法和程序，已经在预备训练三中提出了要求。未能完成预备训练三所布置任务的同学（已经完成的同学，请采用自己的数值计算程序），可参考以下所给出程序。请读懂该程序原理，并根据信号f(t)的不同，设置适当的信号取样间隔T、信号截取范围和频谱分析范围。
数值计算参考程序：

T=0.08;                                     % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+0.8)-heaviside(t-1.2);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
subplot(2,1,1)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(2,1,2)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');
T=0.08;                                     % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+1)-heaviside(t-1);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
subplot(3,2,1)
plot(t,f);
xlabel('t');ylabel('f(t)');title('矩形脉冲');
subplot(3,2,3)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(3,2,5)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');T=0.08;                                     % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+1-0.2)-heaviside(t-1-0.2);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
subplot(3,2,2)
plot(t,f);
xlabel('t');ylabel('f(t)');title('矩形脉冲（平移后）');
subplot(3,2,4)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(3,2,6)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');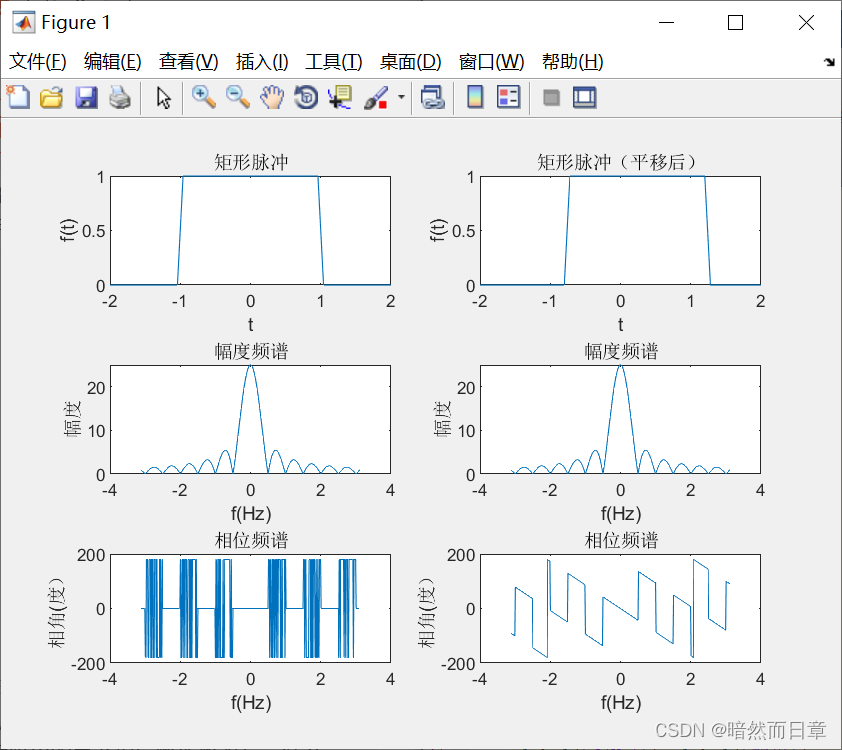

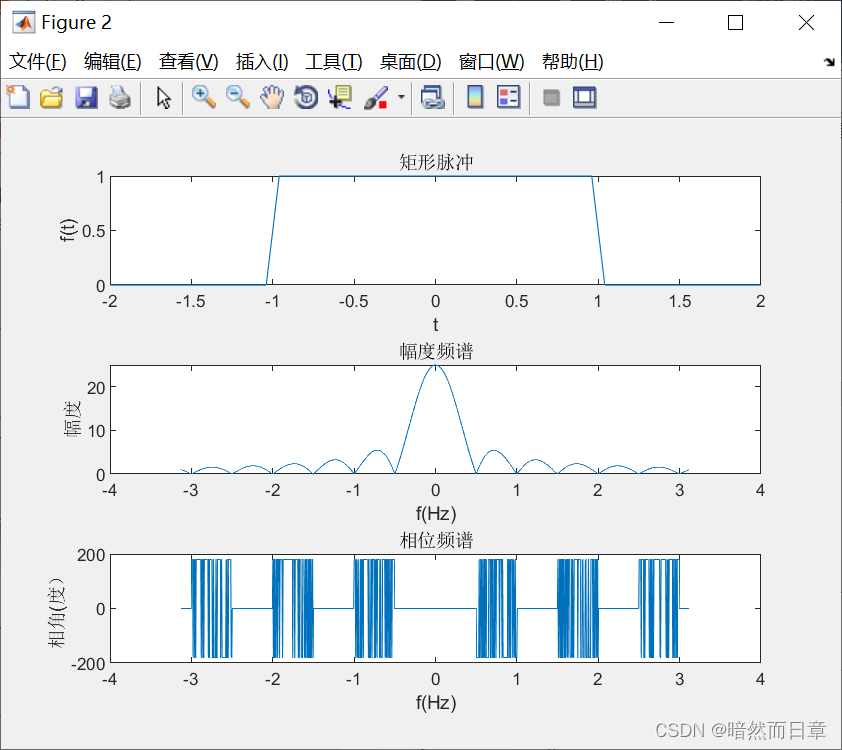
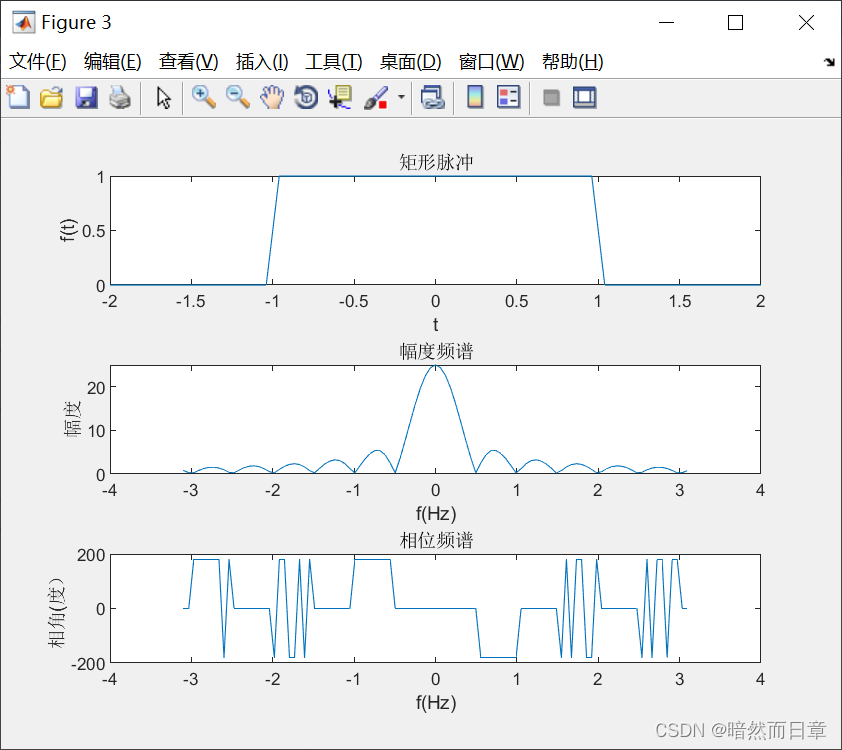
在这里插入图片描述
与符号计算结果相比，数值计算取点间隔较大，会使图形失真，门函数变成斜的 f(t)的相位谱振荡变多。
另外，从频谱图上我们可以看出，在特定位置会发生pi的相位跃变，而且这些跃变对应的是时域上的过零点。MATLAB在进行符号计算时，认为pi和负pi对应的是同一个相位，所以它会把相位为负pi的地方也视为pi。当我们用数值计算时，会产生pi的相位跃变。如果我们忽略这些跃变，那这个相位频谱连起来之后就会是一条直线，其斜率与时移t0有关。

改变T：

T=0.08;                                     % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+1)-heaviside(t-1);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
figure(1)
subplot(3,1,1)
plot(t,f);
xlabel('t');ylabel('f(t)');title('矩形脉冲');
subplot(3,1,2)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(3,1,3)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');T=0.13;                                      % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+1)-heaviside(t-1);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
figure(2)
subplot(3,1,1)
plot(t,f);
xlabel('t');ylabel('f(t)');title('矩形脉冲');
subplot(3,1,2)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(3,1,3)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');T=0.18;                                      % 取样间隔
t=-2:T:2;                                   % 时域截取范围
f=heaviside(t+1)-heaviside(t-1);
W1=pi/T;                                    % 频谱分析范围
N=200;                                      % 频域点数2N+1
k=-N:N;
W=k*W1/(2*N+1);                             % W为频率采样点
F=f*exp(-j*t'*W);                           % 求F(jw)
figure(3)
subplot(3,1,1)
plot(t,f);
xlabel('t');ylabel('f(t)');title('矩形脉冲');
subplot(3,1,2)
plot(W/2/pi,abs(F));
xlabel('f(Hz)');ylabel('幅度');
title('幅度频谱');
subplot(3,1,3)
plot(W/2/pi,angle(F)/pi*180)
xlabel('f(Hz)');ylabel('相角(度）');
title('相位频谱');

T=0.08
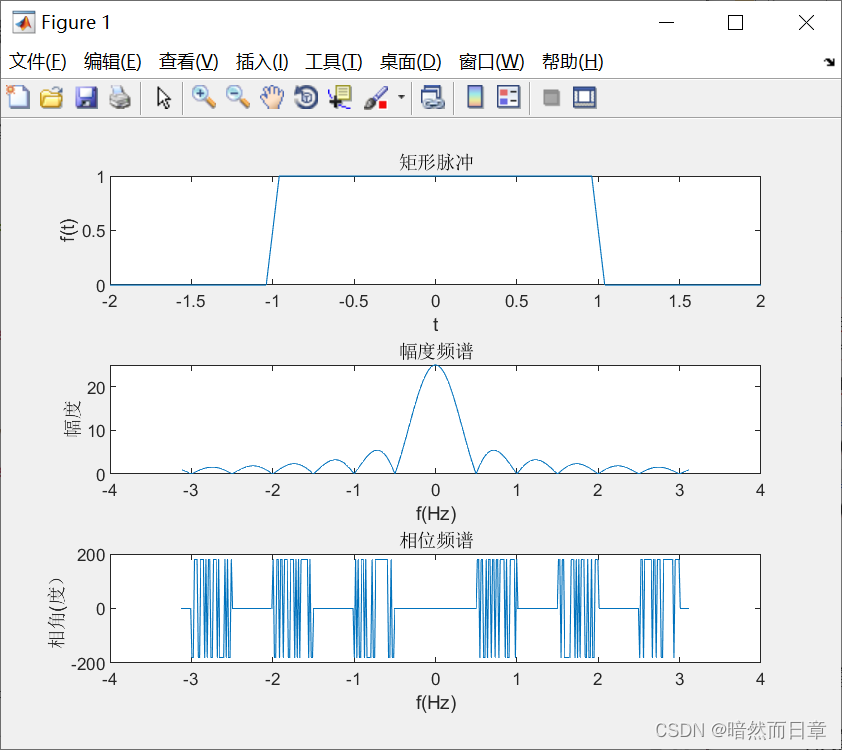
在这里插入图片描述
T=0.13
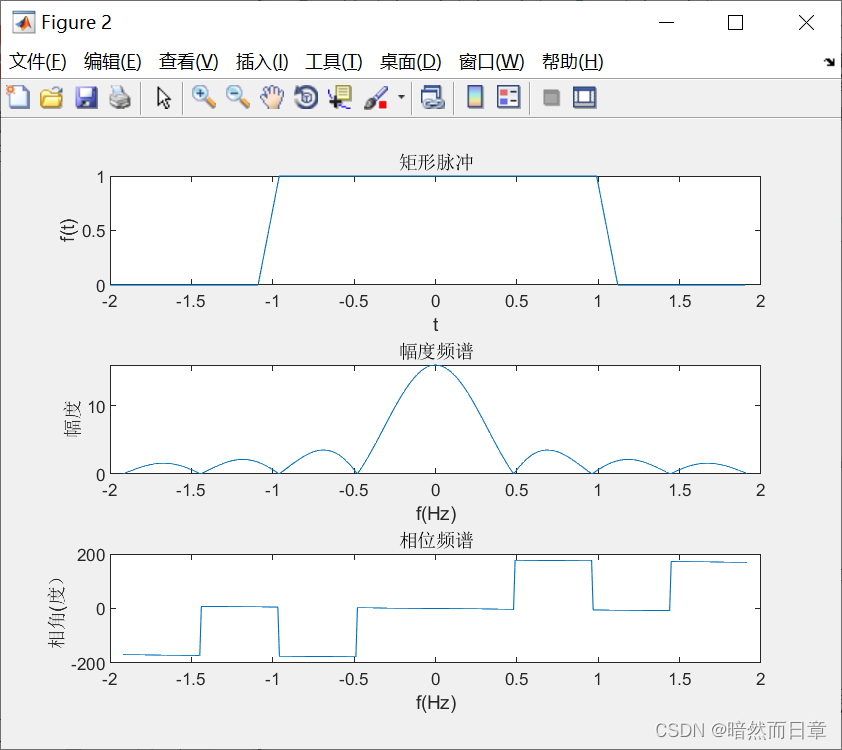
在这里插入图片描述
T=0.28
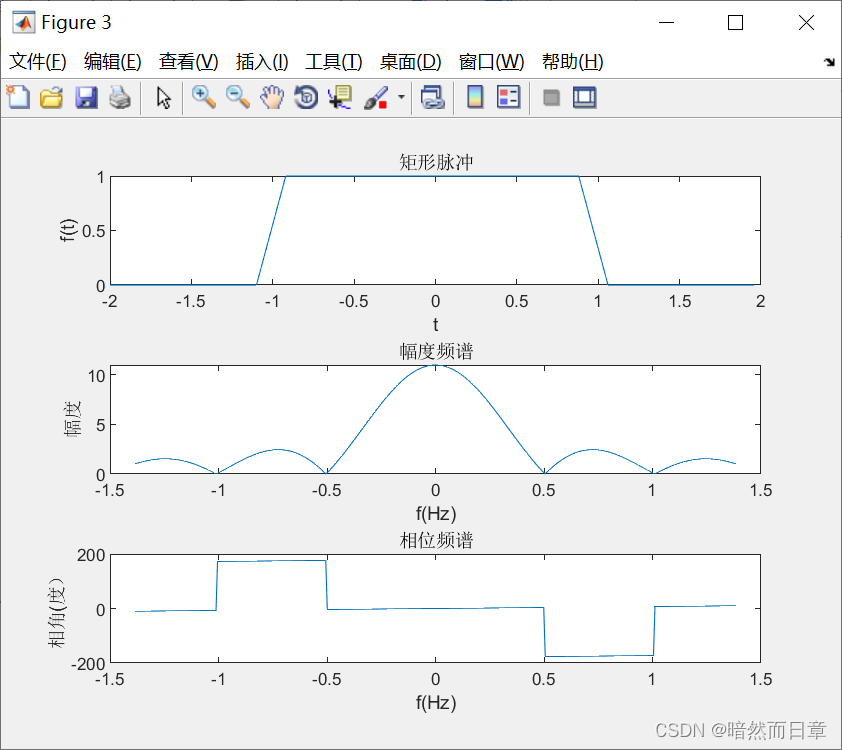
在这里插入图片描述
改变N：
N=200
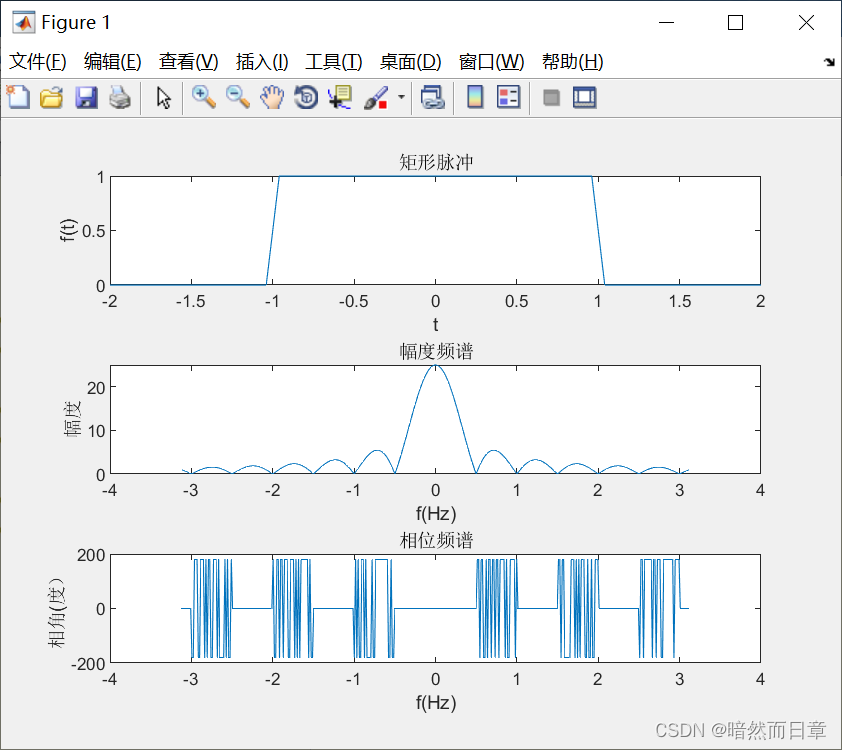
在这里插入图片描述
N=500
在这里插入图片描述
N=50
在这里插入图片描述

3、频谱搬移概念、MATLAB实现，由频域卷积求FT

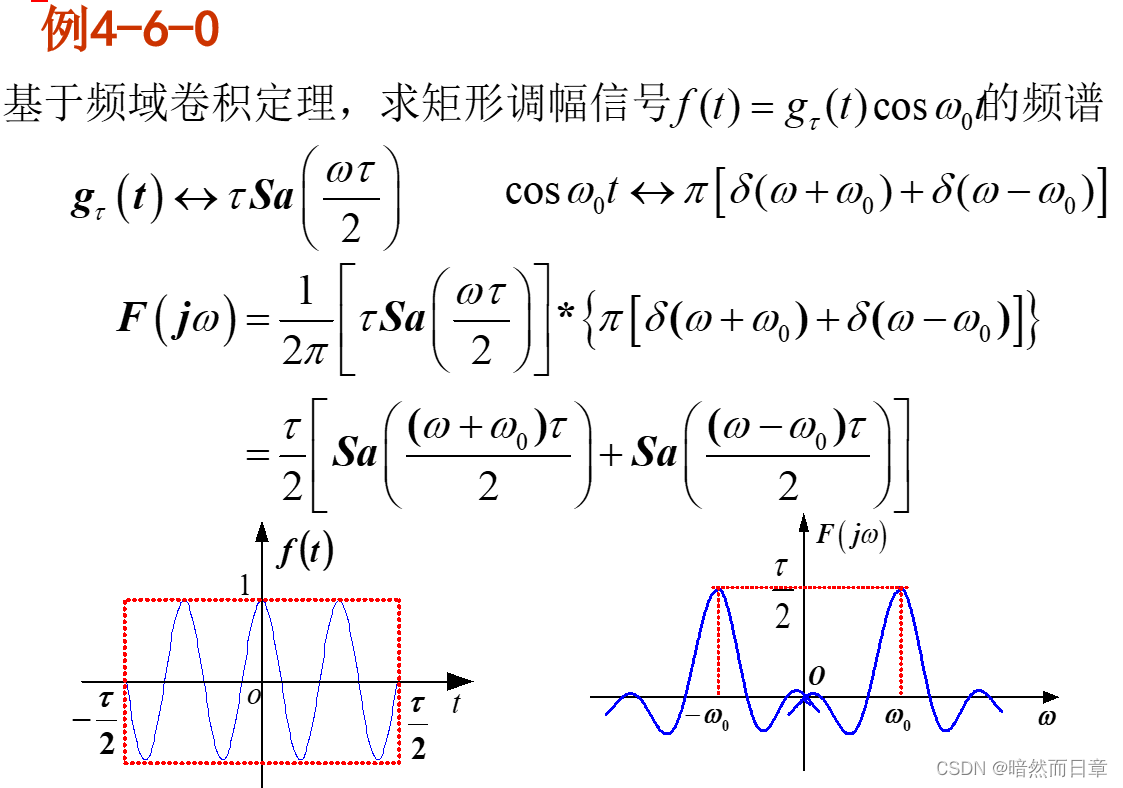
设f(t)为第1题的矩形脉冲，选用一个具有适当频率的余弦信号cos⁡(ω_c t)（请参考课件第98页例4-5-6），用MATLAB画出f(t)cos⁡(ω_c t)的频谱（幅度谱和相位谱合二为一，可自行选择符号计算和数值计算方式，若采用数值计算，需对第2题给出的参考程序略作修改）（第一问）。结合课件例4-5-6，讨论“频谱搬移”（幅度调制）的概念及其实现方法（第二问）。f(t)cos⁡(ω_c t)其实也可以视为f(t)和cos⁡(ω_c t)在时域相乘，根据频域卷积定理（教材式4.5-28）也能得到相同的结论，请基于频域卷积定理推导f(t)cos⁡(ω_c t)的傅里叶变换（参见课件第123页例4-6-0）（第三问）。
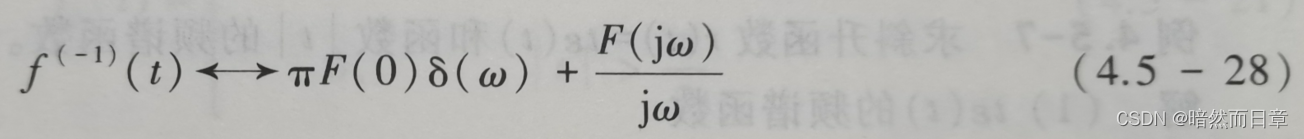
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

（1）

syms t w
gt=heaviside(t+1)-heaviside(t-1);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
subplot(2,1,1);
fplot(t,ft);
set(gca,'XTick',-5:5);
title('信号gt*cos(3*pi*t)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);
xlabel('w');
ylabel('Fjw');
title('频谱');

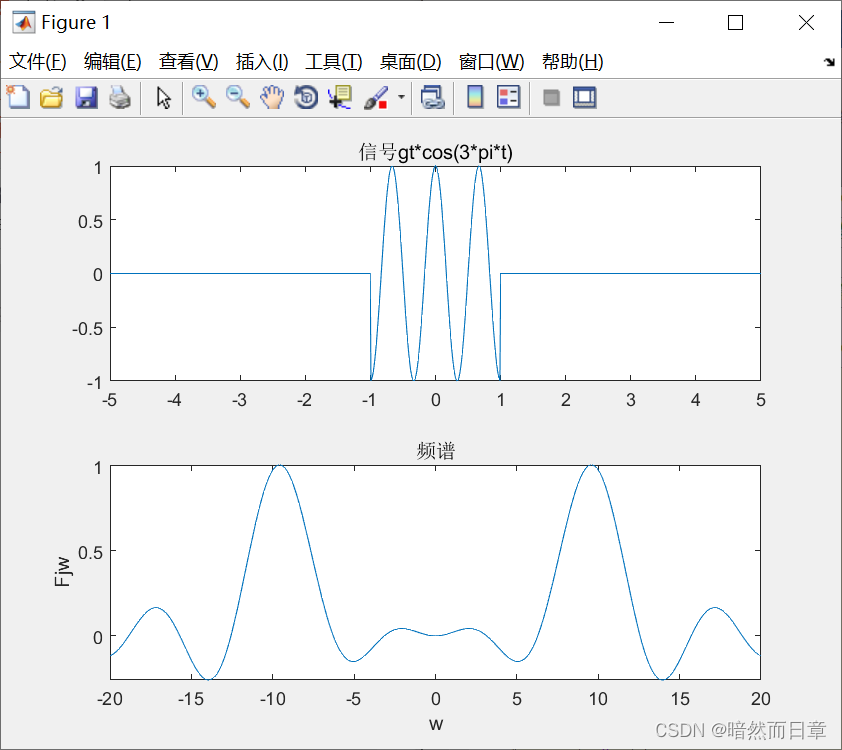
在这里插入图片描述
（2）
频谱搬移概念：频谱搬移是指在发射端将调制信号从低频端搬移到高频端, 便于天线发送或实现不同信号源,不同系统的频分复用。频谱搬移的实质就是要产生两个不同频率（w1,w2）的信号的和频（w1+w2）信号和（或）差频（w1-w2）信号。
实现方法：频谱搬移公式。
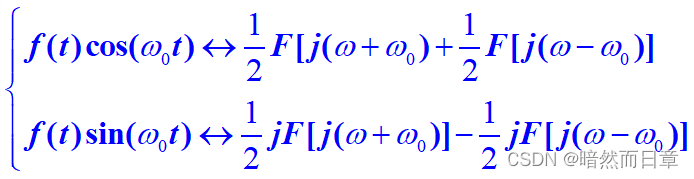
在这里插入图片描述
在这里插入图片描述
（3）
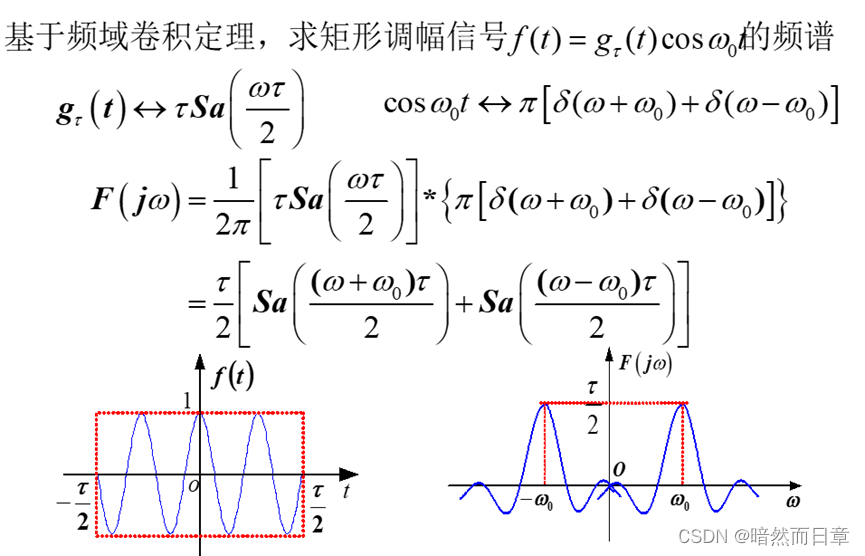
在这里插入图片描述

4、频谱“测不准原理”（加窗的傅里叶变换）

从时域的角度来看，对上一题的f(t)cos⁡(ω_c t)还有另外一种解释：它是利用门函数截取了余弦信号cos⁡(ω_c t)的一段样本。而对这段样本进行傅里叶变换，所得到的频谱上题所示。但是，由周期信号的傅里叶变换可知，cos⁡(ω_c t)的理论频谱应该如教材图4.7-1(a)中所示的两个频域冲激。也就是说，如果只截取cos⁡(ω_c t)的一段样本，来计算cos⁡(ω_c t)的频谱，其结果是不准确的！这种不准确性也称为“测不准原理”，它反映了采用观测的方法来分析信号的频谱所面临的局限性。试分析讨论：①比较上一题求得的f(t)cos⁡(ω_c t)频谱与cos⁡(ω_c t)理论频谱之间的区别与联系。②通过改变矩形脉冲的宽度，截取不同长度的cos⁡(ω_c t)样本，用MATLAB分别分析其频谱，比较不同长度样本频谱的差异，分析若想改善频谱分析的准确性，应该如何选取样本长度？
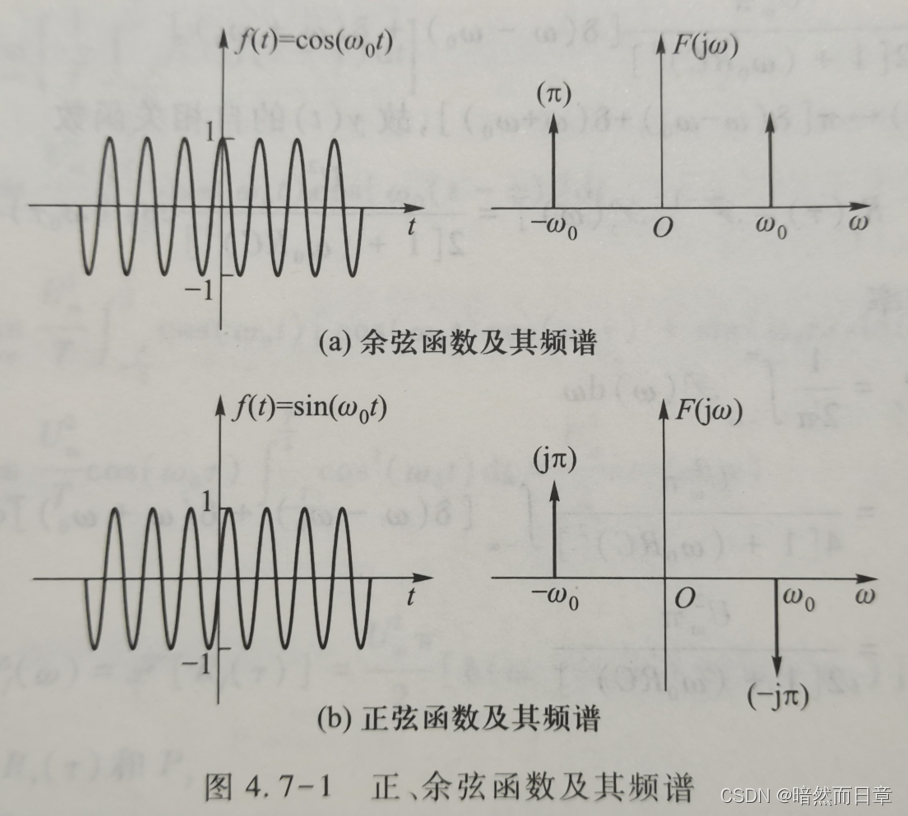
在这里插入图片描述

（1）
区别：f(t)cos⁡(ω_c t)理论频谱的频带与cos⁡(ω_c t)频谱的频带相比压缩了。
联系：f(t)cos⁡(ω_c t)理论频谱的频带是成比例压缩的。
（2）

syms t w
gt=heaviside(t+1)-heaviside(t-1);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(1)
subplot(2,1,1);
fplot(t,ft,[-2,2]);title('信号cos(3*pi*t)加长度为2的窗')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');syms t w
gt=heaviside(t+2)-heaviside(t-2);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(2)
subplot(2,1,1);
fplot(t,ft,[-4,4]);title('信号cos(3*pi*t)加长度为4的窗)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');syms t w
gt=heaviside(t+5)-heaviside(t-5);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(3)
subplot(2,1,1);
fplot(t,ft,[-10,10]);title('信号cos(3*pi*t)加长度为10的窗)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');syms t w
gt=heaviside(t+10)-heaviside(t-10);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(4)
subplot(2,1,1);
fplot(t,ft,[-20,20]);title('信号cos(3*pi*t)加长度为20的窗)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');syms t w
gt=heaviside(t+25)-heaviside(t-25);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(5)
subplot(2,1,1);
fplot(t,ft,[-50,50]);title('信号cos(3*pi*t)加长度为50的窗)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');syms t w
gt=heaviside(t+100)-heaviside(t-100);
ft=gt*cos(3*pi*t);
Fjw=fourier(ft);
figure(6)
subplot(2,1,1);
fplot(t,ft,[-200,200]);title('信号cos(3*pi*t)加长度为200的窗)')
subplot(2,1,2);
fplot(w,Fjw,[-20,20]);xlabel('w');ylabel('Fjw');title('频谱');

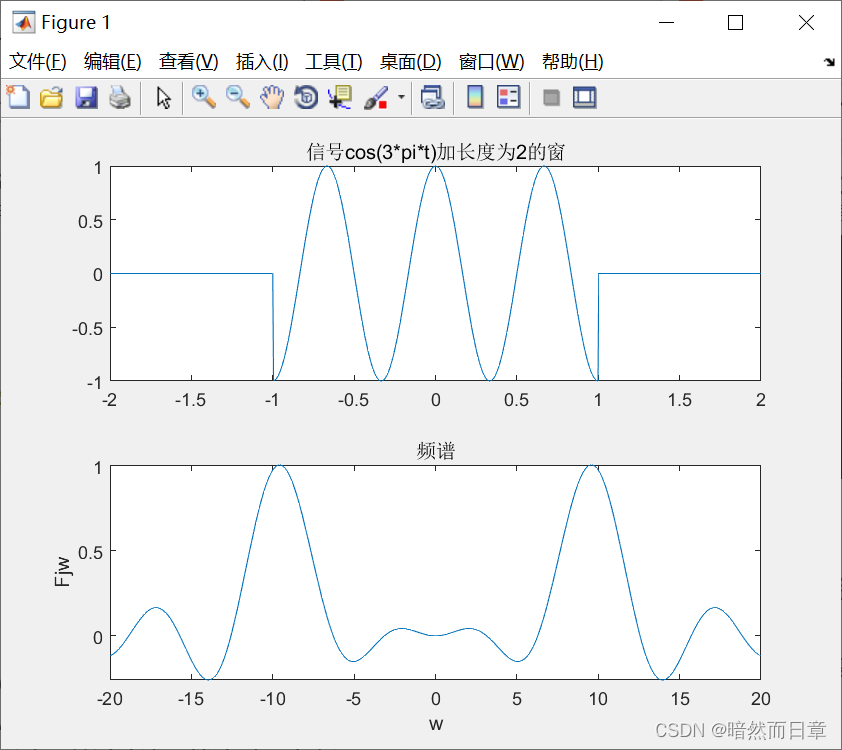
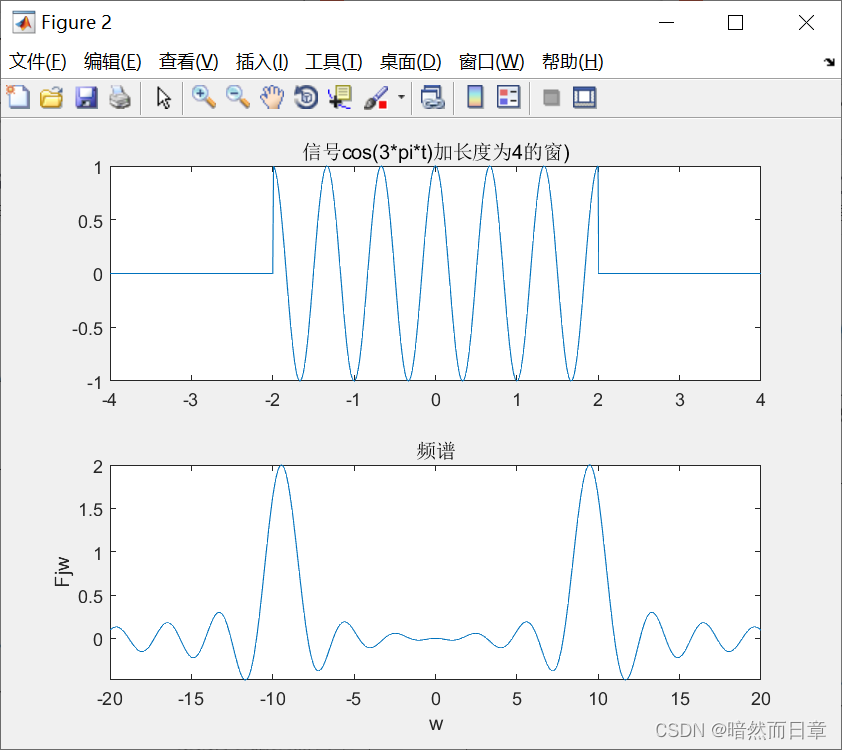
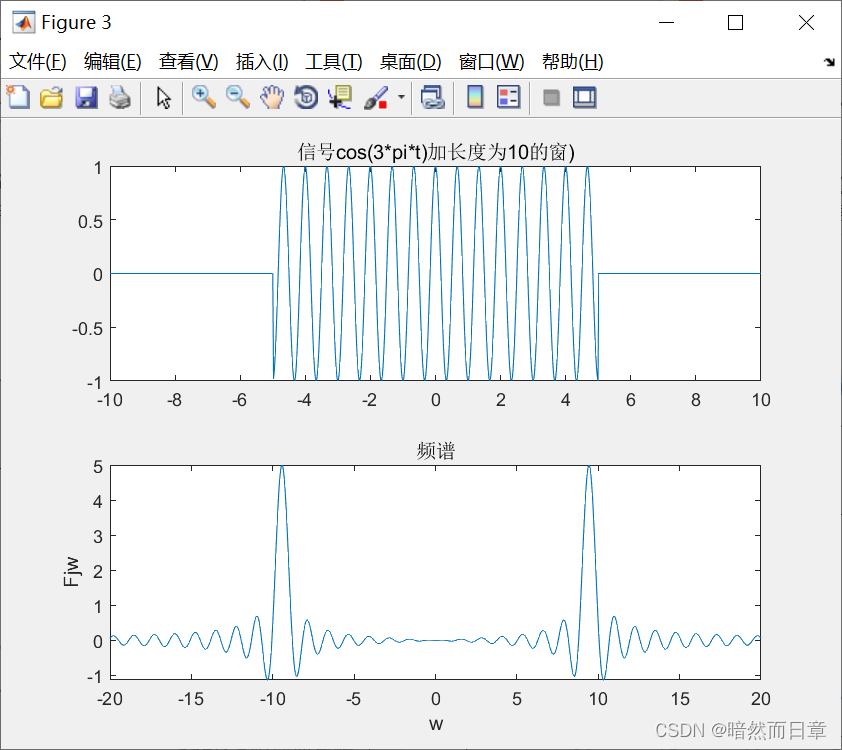
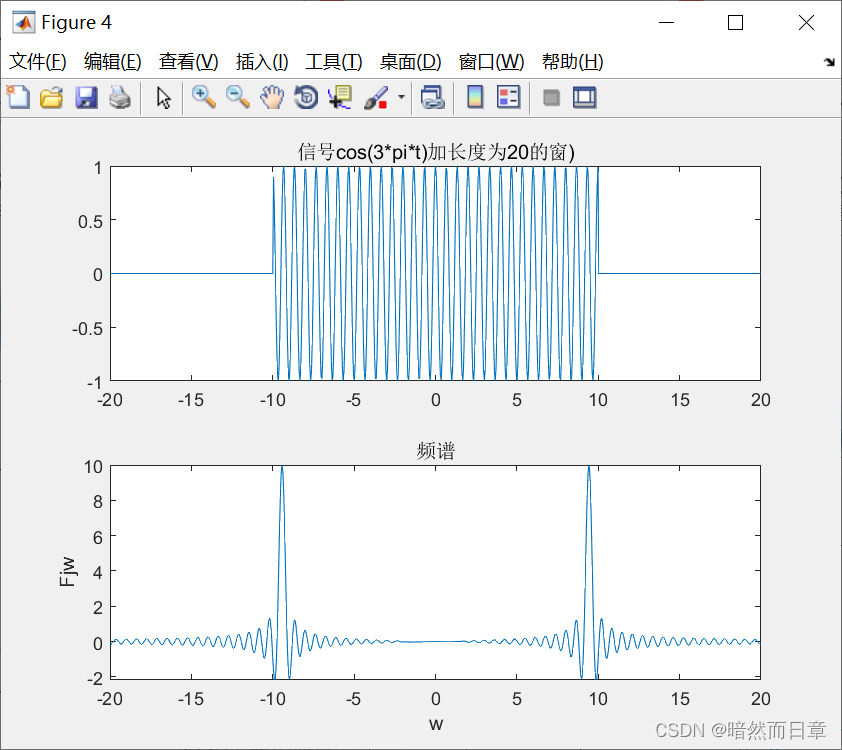
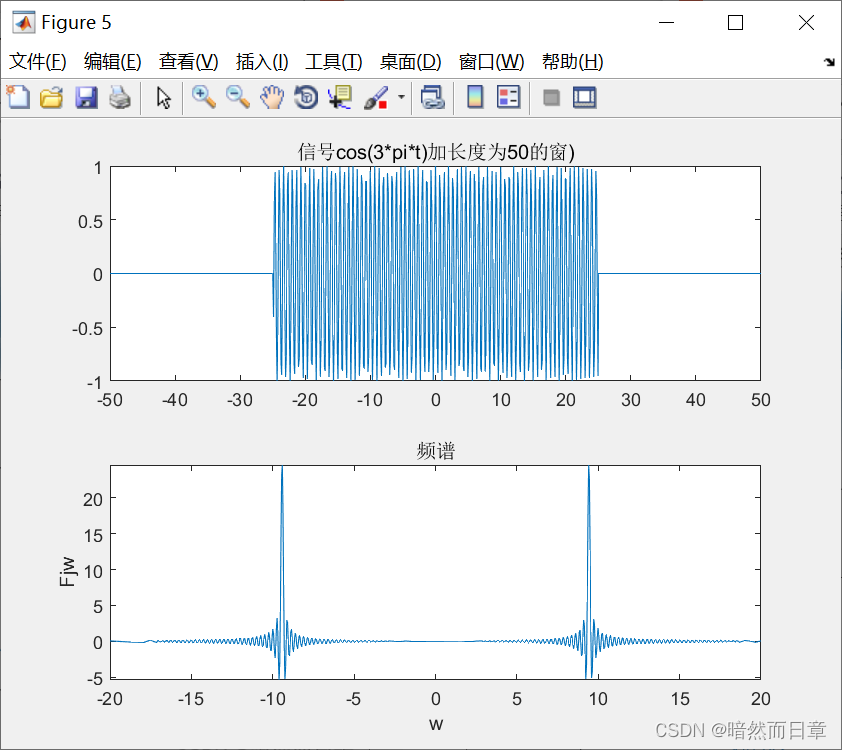
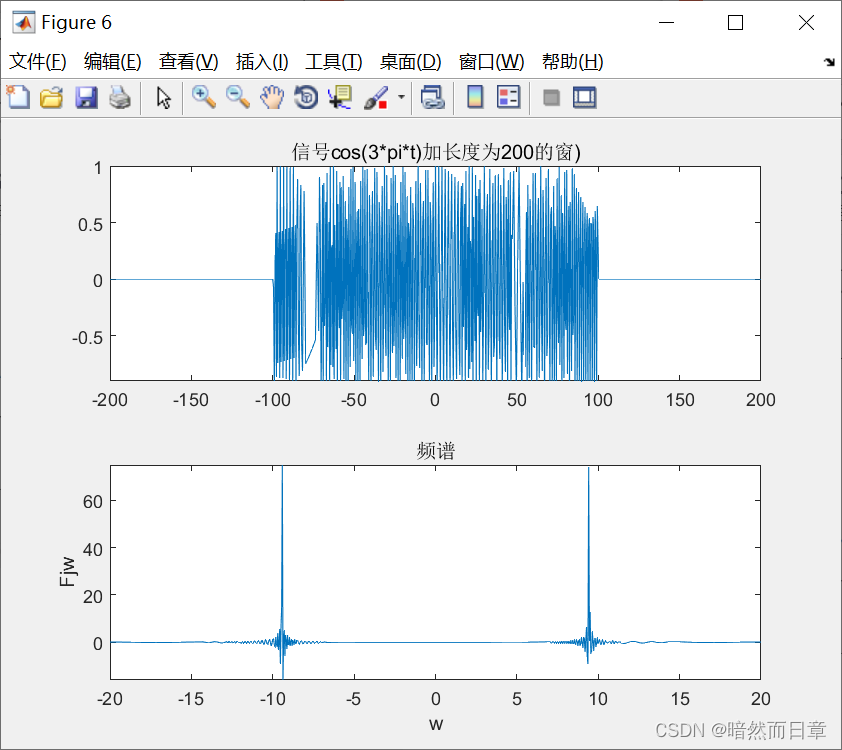
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
矩形脉冲宽度越大，截取长度越长，越准确。

5、时域尺度变换对傅里叶变换的影响

分别针对前面各题的矩形脉冲f(t)、余弦信号cos⁡(ω_c t)以及f(t)cos⁡(ω_c t)，分别进行时域尺度变换（变换系数自定），采用MATLAB符号或者数值计算，求尺度变换后的频谱。根据结果总结时域尺度变换对频谱的影响，并讨论这一结论对于确定通信系统的带宽有何意义？

syms t w
f(t)=heaviside(t+1)-heaviside(t-1);
Fjw=fourier(f(t));
fai=log(Fjw/abs(Fjw))/1i;
subplot(2,2,1)
fplot(t,f(t));set(gca,'XTick',-5:5);
xlabel('t');ylabel('f(t)'); title('f(t)')
subplot(2,2,2)
fplot(w/2/pi,abs(Fjw),[-20,20]);
xlabel('f(HZ)');ylabel('幅度'); title('矩形脉冲信号的频谱')syms t w
f(t)=heaviside(2*t+1)-heaviside(2*t-1);
Fjw=fourier(f(t));
fai=log(Fjw/abs(Fjw))/1i;
subplot(2,2,3)
fplot(t,f(t));set(gca,'XTick',-5:5);
xlabel('t');ylabel('f(2t)'); title('f(2t)')
subplot(2,2,4)
fplot(w/2/pi,abs(Fjw),[-20,20]);
xlabel('f(HZ)');ylabel('幅度'); title('变换后的频谱');

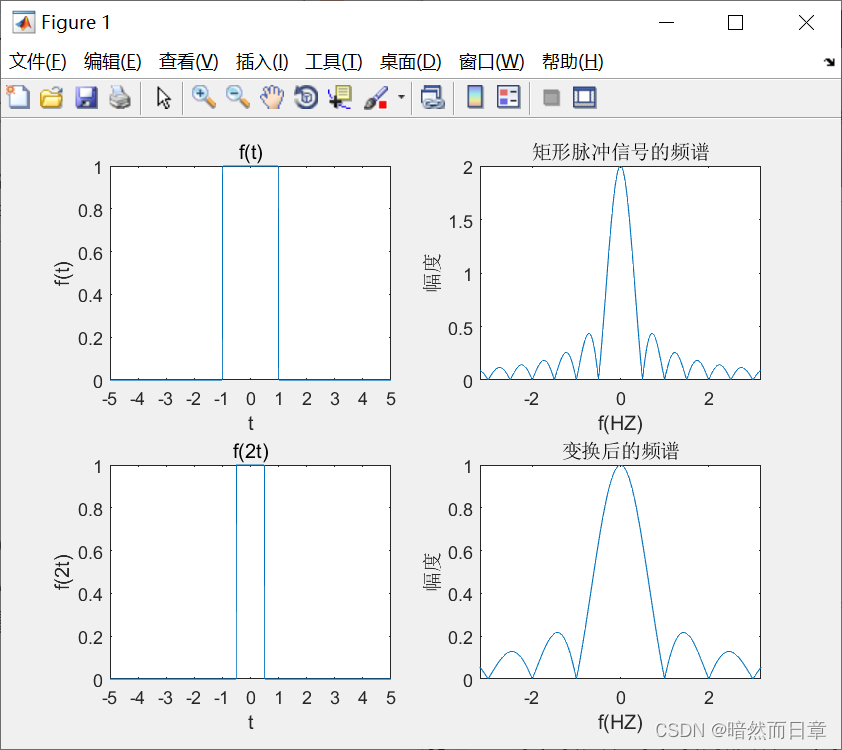
在这里插入图片描述
在这里插入图片描述

6、傅里叶变换的对称性质

什么是傅里叶变换的对称性质？利用该性质，求解习题4.17。（第一问）若用门函数g_τ (⋅)来表示幅度为1、宽度为τ的对称矩形脉冲，则g_2 (t)的傅里叶变换是什么？g_2 (jω)的傅里叶反变换是什么？（第二问）
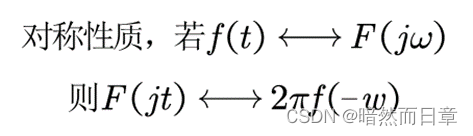
在这里插入图片描述

（1）
在这里插入图片描述
求解4.17

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

7、傅里叶变换的微分性质和时域卷积定理

分别利用傅里叶变换的微分性质和时域卷积定理，求图示对称三角形脉冲的傅里叶变换（理论计算），并用MATLAB画出其频谱（幅度相位谱合二为一）。（提示：三角形脉冲可以表示为两个宽度相同的矩形脉冲的卷积）
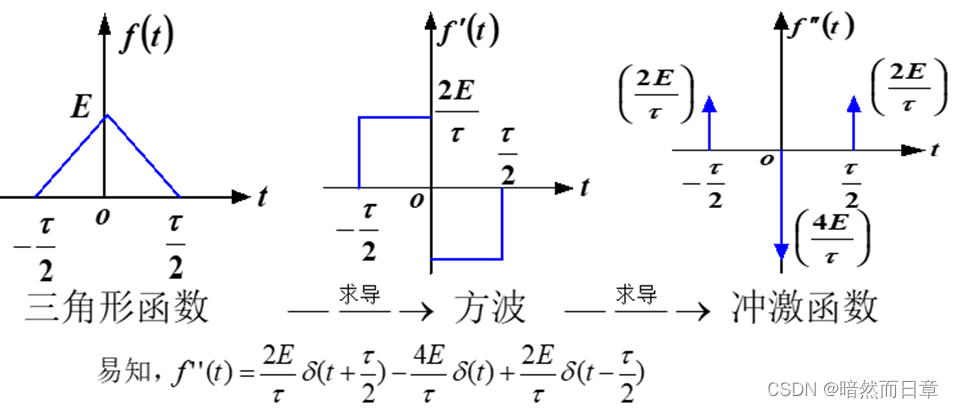
在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
E=2，τ=2时

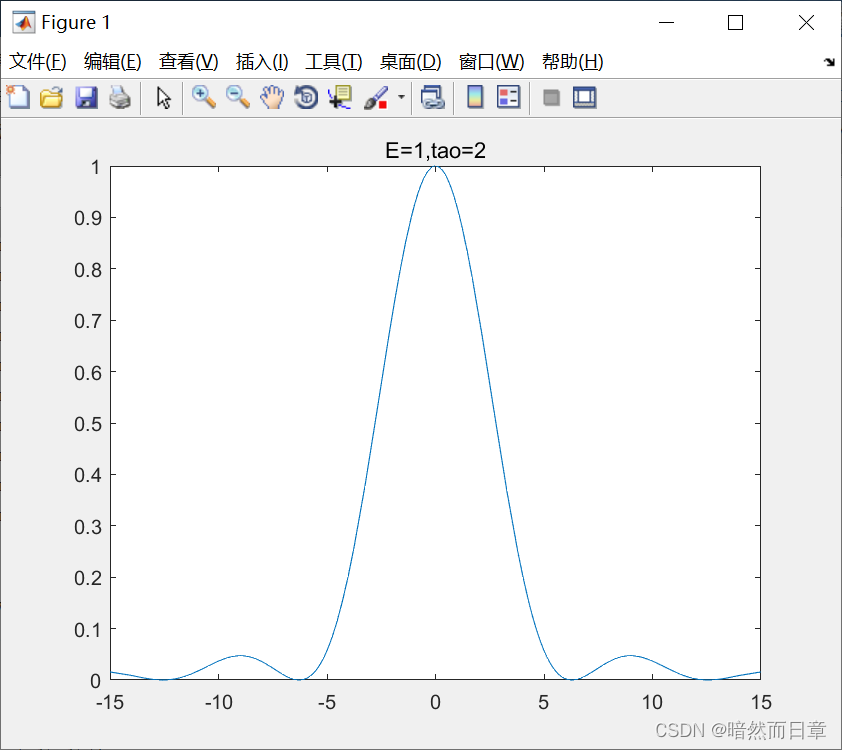
syms w;
Fjw=sinc(0.5*w/pi)^2;
fplot(w,Fjw,[-15,15]);
title('E=1,tao=2');

在这里插入图片描述

三、反思总结

暂无

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.hqwc.cn/news/297268.html

如若内容造成侵权/违法违规/事实不符，请联系编程知识网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

Echarts社区推荐

Echarts社区推荐

Apache Echarts官方示例中，有的demo并不能完全符合我们的需求，下面推荐几个Echarts社区，以便快速搭建项目。 1. isqqw 官方地址 ：https://www.isqqw.com/ 2. makepie 官方地址 ：https://www.makeapie.cn/echarts 3. P…
阅读更多...
神经网络：深度学习优化方法

神经网络：深度学习优化方法

1.有哪些方法能提升CNN模型的泛化能力 采集更多数据：数据决定算法的上限。 优化数据分布：数据类别均衡。 选用合适的目标函数。 设计合适的网络结构。 数据增强。 权值正则化。 使用合适的优化器等。 2.BN层面试高频问题大汇总 BN层解决了什么问…
阅读更多...
2024年【陕西省安全员C证】考试总结及陕西省安全员C证复审考试

2024年【陕西省安全员C证】考试总结及陕西省安全员C证复审考试

题库来源：安全生产模拟考试一点通公众号小程序 陕西省安全员C证考试总结考前必练！安全生产模拟考试一点通每个月更新陕西省安全员C证复审考试题目及答案！多做几遍，其实通过陕西省安全员C证模拟考试题库很简单。 1、【多选题】下列…
阅读更多...
基于SpringBoot的瑜伽馆管理系统 JAVA简易版

基于SpringBoot的瑜伽馆管理系统 JAVA简易版

目录 一、摘要1.1 项目介绍1.2 项目录屏 二、功能模块2.1 数据中心模块2.2 瑜伽课程模块2.3 课程预约模块2.4 系统公告模块2.5 课程评价模块2.6 瑜伽器械模块 三、系统设计3.1 实体类设计3.1.1 瑜伽课程3.1.2 瑜伽课程预约3.1.3 系统公告3.1.4 瑜伽课程评价 3.2 数据库设计3.2.…
阅读更多...
Python时间复杂度计算题答案

Python时间复杂度计算题答案

评论 题目链接 https://blog.csdn.net/qq_33254766/article/details/132255078 答案 时间复杂度：O(n)。 分析：这段代码遍历了n次，所以时间复杂度是线性的，即O(n)。 时间复杂度：O(n^2)。 分析：两个嵌套的…
阅读更多...
Kioptrix-2

Kioptrix-2

环境搭建 这个靶场环境稍微有点麻烦，首次打开的时候，需要将靶机从VM中移除（注意是 从VM里面移除），然后利用nodpad等工具打开vmx文件，然后两步： 所有以“ethernet0”开头的条目并保存更改。然后…
阅读更多...
基于Qt之QChart 图表（优美的曲线图案例）

基于Qt之QChart 图表（优美的曲线图案例）

## 项目演示 平台：ubuntu18.04 Qt版本：QT5.14.2 源码位置GitCode：https://gitcode.com/m0_45463480/QCharts/tree/main ## QChart 图表 自从 Qt 发布以来，给跨平台的用户带来很多便利。在 Qt5.7 之前，Qt 在开源社区版本里没有 Qt Charts（自带的绘图组件库）。这使得像…
阅读更多...
抖店一件代发实操，干货满满！

抖店一件代发实操，干货满满！

我是电商珠珠 没有货源的新手，在店铺刚开始的时候可以搞无货源模式，也就是一件代发，去搬运别人店铺的商品到自己店铺，再去利用信息差去赚取差价。 很多人不知道具体要怎么做，今天我就来给大家讲一讲。 一、入驻 入…
阅读更多...
超维空间S2无人机使用说明书——43、将雷达定位信息通过mavros传给飞控

超维空间S2无人机使用说明书——43、将雷达定位信息通过mavros传给飞控

引言：在实现三维雷达定位后，还需要将定位数据传给飞控，这样无人机才能实现切入定点模式。无人机在有了位置以后，才能实现精确的闭环控制 简介 采用fast-lio定位算法，通过修改源码直接发布定位出来的位置信息和速度信…
阅读更多...
分享 | 软件测试的基本流程是什么？软件测试流程详细介绍

分享 | 软件测试的基本流程是什么？软件测试流程详细介绍

软件测试 软件测试和软件开发一样，是一个比较复杂的工作过程，如果无章法可循，随意进行测试势必会造成测试工作的混乱。为了使测试工作标准化、规范化，并且快速、高效、高质量地完成测试工作，需要制订完整且具体的测试…
阅读更多...
10.3 uinput

10.3 uinput

uinput 简介 uinput 是一个内核驱动，应用程序通过它可以在内核中模拟一个输入设备，其设备文件名是 /dev/uinput 或 /dev/input/uinput。 uinput 使用 使用 uinput 时遵循以下步骤： 通过 open 打开 uinput 设备通过 ioctl 设置属性位图通过…
阅读更多...
前端---html 的介绍

前端---html 的介绍

1. 网页效果图 --CSDN 2. html的定义 HTML 的全称为&#xff1a;HyperText Mark-up Language, 指的是超文本标记语言。 标记&#xff1a;就是标签, <标签名称> </标签名称>, 比如: <html></html>、<h1></h1> 等&#xff0c;标签大多数都是…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023