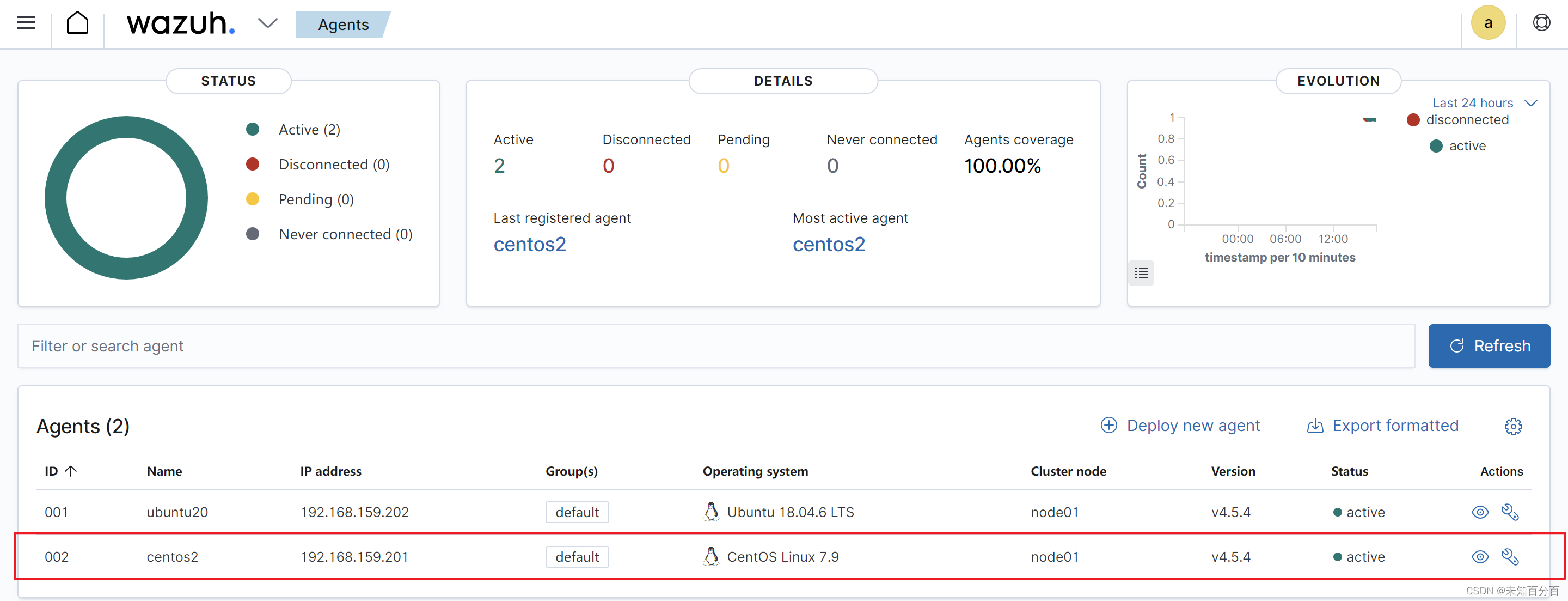
第一次作业
1.下列序列是图序列的是( )
A.1,2,2,3,4,4,5
B.1,1,2,2,4,6,6
C.0,0,2,3,4,4,5
D.2,2,2,2,2,2,2
2.具有3个顶点互不同构的图有( )个
A.4 B.3 C.2 D.1
3.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则 d ( v 1 ) = () d(v_1)=( ) d(v1)=()
A.4 B.3 C.2 D.1
4.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则顶点导出子图 G [ { v 1 , v 2 , v 3 } ] G[\{v_1,v_2,v_3\}] G[{v1,v2,v3}] 中有( )条边
A.5 B.4 C.3 D.2
5.设图 G = ( V , E ) G=(V,E) G=(V,E),其中 V = { v 1 , v 2 , v 3 , v 4 } V=\{v_1,v_2,v_3,v_4\} V={v1,v2,v3,v4}, E = { v 1 v 2 , v 1 v 3 , v 1 v 1 , v 2 v 4 , v 3 v 4 } E=\{v_1v_2,v_1v_3,v_1v_1,v_2v_4,v_3v_4\} E={v1v2,v1v3,v1v1,v2v4,v3v4},则边导出子图 G [ { v 1 v 1 , v 2 v 4 } ] G[\{v_1v_1,v_2v_4\}] G[{v1v1,v2v4}] 是图 G G G 的支撑子图。该说法( )。
A.正确 B.错误
6.若图 G G G 存在 ( u , v ) (u,v) (u,v) 闭途径,则图 G G G 中也一定存在 ( u , v ) (u,v) (u,v) 闭迹。该说法( )。
A.正确 B.错误
7.互不同构的 4 4 4 阶连通图有( )个。
A.6 B.5 C.4 D.3
8.在一个化学实验室里,有 n n n 个药箱,其中每两个不同的药箱恰有一种相同的化学品,而且每种化学品恰好在两个药箱中出现,则每个药箱有( )种化学品;这 n n n 个药箱种共有( )种不同的化学品。
9.平面上有 n n n 个点 S = { p 1 , p 2 , . . . , p n } S=\{p_1,p_2,...,p_n\} S={p1,p2,...,pn},其中任何两个点之间的距离至少是 1 1 1,证明这 n n n 个点中距离为 1 1 1 的点对数不超过 3 n 3n 3n。
证明:
第二次作业
1.每对顶点都相邻的图是完全图。该说法( )。
A.正确 B.错误
2.(多选)设聚会有 n n n 人参加,已知聚会中要么有 3 3 3 个人互相都认识,要么有 3 3 3 个人相互都不认识,则参与这次聚会的人数 n n n 可能是( )。
A.7 B.6 C.5 D.4
3.如下图 G G G 是著名的 P e t e r s e n Petersen Petersen 图,关于此图说法正确的是( )。

A.它是二部图 B.它不是二部图
4.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 , v 4 } , A = { ( v 1 , v 2 ) , ( v 3 , v 4 ) , ( v 1 , v 1 ) , ( v 2 , v 4 ) , ( v 3 , v 4 ) } V=\{v_1,v_2,v_3,v_4\},A=\{(v_1,v_2),(v_3,v_4),(v_1,v_1),(v_2,v_4),(v_3,v_4)\} V={v1,v2,v3,v4},A={(v1,v2),(v3,v4),(v1,v1),(v2,v4),(v3,v4)},则 d + ( v 1 ) = d^+(v_1)= d+(v1)=( )
A.4 B.3 C.2 D.1
5.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 , v 4 } , A = { ( v 1 , v 2 ) , ( v 3 , v 4 ) , ( v 1 , v 1 ) , ( v 2 , v 4 ) , ( v 3 , v 4 ) } V=\{v_1,v_2,v_3,v_4\},A=\{(v_1,v_2),(v_3,v_4),(v_1,v_1),(v_2,v_4),(v_3,v_4)\} V={v1,v2,v3,v4},A={(v1,v2),(v3,v4),(v1,v1),(v2,v4),(v3,v4)},则它有( )个强连通分支。
A.4 B.3 C.2 D.1
6.任何长为奇数的闭途径中一定包含长为奇数的圈。该说法( )。
A.正确 B.错误
7.某次聚会很特别,在这次聚会中,每两个互相认识的人,都没有共同的熟人,但,每两个互不认识的人都恰有两个共同的熟人。有人宣称这次聚会的参加者一定有同样数目的熟人他的说法( )
A.正确 B.错误
8.完全二部图 K m , n K_{m,n} Km,n中有( )条边。
9.构造一个 7 7 7 阶 4 4 4 正则简单图。
第三次作业
1.设 A ( G ) = A(G)= A(G)=
( 1 2 0 2 2 1 0 1 3 ) (3) \begin{pmatrix} 1 & 2 & 0 \\ 2 & 2 & 1 \\ 0 & 1 & 3 \end{pmatrix} \tag{3} 120221013 (3),则顶点 v 1 v_1 v1 的度 d ( v 1 ) = d(v_1)= d(v1)=
A.5 B.4 C.3
2.设 A ( G ) = A(G)= A(G)=
( 1 2 0 2 2 1 0 1 3 ) (3) \begin{pmatrix} 1 & 2 & 0 \\ 2 & 2 & 1 \\ 0 & 1 & 3 \end{pmatrix} \tag{3} 120221013 (3),则顶点 v 2 v_2 v2 到 v 2 v_2 v2 且长为 2 2 2 的不同路径有( )条。
A.9 B.8 C.7 D.6
3.设 A ( G ) = A(G)= A(G)=
( 0 0 1 2 1 1 1 3 0 ) (3) \begin{pmatrix} 0 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 3 & 0 \end{pmatrix} \tag{3} 021013110 (3),则有向图 D D D 中的有向边 ( v 2 , v 3 ) (v_2,v_3) (v2,v3) 有( )条。
A.3 B.2 C.1 D.0
4.设有向图 D = ( V , A ) D=(V,A) D=(V,A),其中 V = { v 1 , v 2 , v 3 } , A = { ( v 1 , v 2 ) , ( v 1 , v 3 ) , ( v 2 , v 3 ) , ( v 3 , v 2 ) } V=\{v_1,v_2,v_3\},A=\{(v_1,v_2),(v_1,v_3),(v_2,v_3),(v_3,v_2)\} V={v1,v2,v3},A={(v1,v2),(v1,v3),(v2,v3),(v3,v2)},则关联矩阵 M ( D ) = M(D)= M(D)=( )
A. [ 1 1 0 0 − 1 0 1 − 1 0 − 1 − 1 1 ] \begin{bmatrix} 1 & 1 & 0 & 0 \\ -1 & 0 & 1 & -1 \\ 0 & -1 & -1 & 1 \end{bmatrix} 1−1010−101−10−11
B. [ − 1 − 1 0 0 1 0 − 1 1 0 1 1 − 1 ] \begin{bmatrix} -1 & -1 & 0 & 0 \\ 1 & 0 & -1 & 1 \\ 0 & 1 & 1 & -1 \end{bmatrix} −110−1010−1101−1
C. [ 1 1 0 0 1 0 1 1 0 1 1 1 ] \begin{bmatrix} 1 & 1 & 0 & 0 \\ 1 & 0 & 1 & 1 \\ 0 & 1 & 1 & 1 \end{bmatrix} 110101011011
5.设 G G G 如下图所示,则 ε ( G − v ) = \varepsilon(G-v)= ε(G−v)= ( )

A.8 B.6 C.4 D.2
6.设 G 1 , G 2 G_1,G_2 G1,G2 分别如下图所示,则 v ( G 1 ∪ G 2 ) = v(G_1 \cup G_2)= v(G1∪G2)=( )

A.5 B.4 C.3 D.2
7.设 G G G 如下图所示,则 G ⋅ e G·e G⋅e 的基础简单图有( )条边。

A.11 B.10 C.9 D.8
8.求下图 v 1 v_1 v1 到 v 2 v_2 v2 的最短路( )。

9.判断下图能否转化为笛卡尔积的形式,简述理由。

第四次作业
1.互不同构的六阶树有( )个。
A.10 B.8 C.6 D.4
2.已知 G G G 为简单图,且 v ( G ) = ε ( G ) = 2023 v(G)=\varepsilon(G)=2023 v(G)=ε(G)=2023,下列说法正确的是( )。
A. G G G 中一定有圈
B. G G G 一定连通
C. G G G 中不一定有圈
D. G G G 不一定联通
3.(多选)下列选项中有可能是树图的度序列的有 ()
A.(1,2,2,2,2,3)
B.(0,1,1,2,3,3)
C.(1,1,1,2,2,3)
D.(1,1,1,1,2,4)
4.(多选)设 G G G 是连通图, e ∈ E ( G ) e \in E(G) e∈E(G),则 w ( G − e ) w(G -e) w(G−e) 可能是( )
A.1 B.2 C.3 D.4
5.设图 G G G 有 v v v 个顶点、 ε \varepsilon ε 条边和 ω \omega ω 个连通分支, G G G 中不同圈的个数为 n n n,则下列关于 n n n 的说法最恰当的是( )。
A. n ≥ ε − v n \geq \varepsilon-v n≥ε−v
B. n ≥ ε − v + ω n \geq \varepsilon-v+\omega n≥ε−v+ω
C. n ≤ ε − v − ω n \leq \varepsilon-v-\omega n≤ε−v−ω
D. n ≤ v − ω n \leq v-\omega n≤v−ω
6.设 G G G 如下图所示,则 τ ( G ) = \tau(G)= τ(G)=( )。

A.8 B.6 C.5 D.4
7. τ ( K 5 ) = \tau(K_5)= τ(K5)=( )。
A. 5 10 5^{10} 510 B. 5 8 5^8 58 C. 5 5 5^5 55 D. 5 3 5^3 53
8.设 G G G 如下图所示,则 G G G 中含有边 e e e 的支撑树有( )。

9.设 T T T 是一棵树,其平均度为 α \alpha α,求 v ( T ) v(T) v(T)。