题目描述

​ 将一个８*８的棋盘进行如下分割：将原棋盘割下一块矩形棋盘并使剩下部分也是矩形，再将剩下的部分继续如此分割，这样割了(n−1)次后，连同最后剩下的矩形棋盘共有 n 块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)

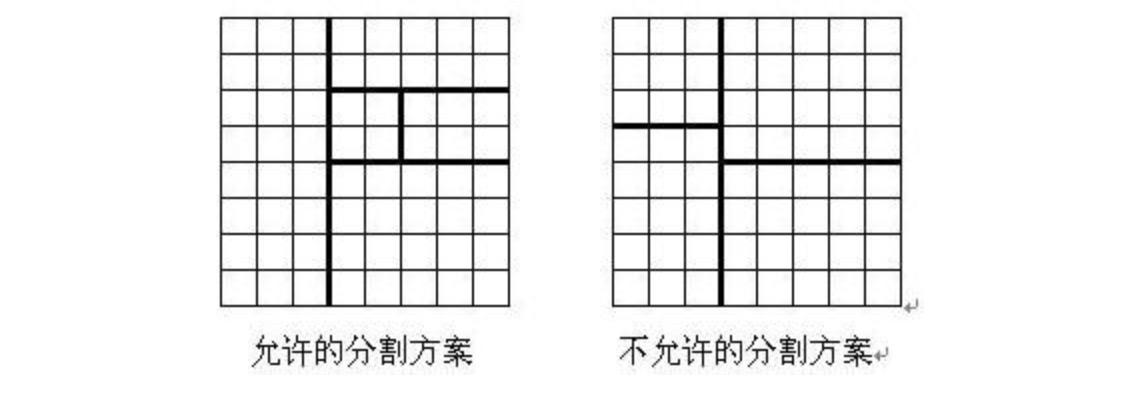
​ 原棋盘上每一格有一个分值，一块矩形棋盘的总分为其所含各格分值之和。现在需要把棋盘按上述规则分割n块矩形棋盘，并使各矩形棋盘总分的平方和最小。

​ 请编程对给出的棋盘及 n，求出平方和的最小值。

---

输入

​ 第1行为一个整数n(1<n<15)。

​ 第2行至第9行每行为8个小于100的非负整数，表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。

输出

​ 仅一个数，为最小的平方和值。

输入样例1

3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3

输出样例1

1460

---

数据规模与限定

时间限制：1 s

内存限制：64 M

解题分析

理解题意后，我们发现，我们每次只能横着切或者竖着切，并且切割下来的棋盘不能再次进行切割，然后题目要求我们去计算所有格子的分值之和的平方，这就考验了我们一个重要的思想，前缀和思想，如果我们每次都去一个一个地加和，那么时间必然消耗很多，所以这里考验我们会使用的第一个小技巧就是前缀和思想。我们不妨设定一个Val[i][j]的二维数组，表示从(1,1)到(i,j)的全部棋盘上的数值之和，根据这个定义，我们很快就可以得知，如果要求(i,j)到(k,l)区间上所有的格子分值总和的公式是Val[i][j]-Val[i][l-1]-Val[k-1][j]+Val[k-1][l-1]。这个公式其实不难理解，画个图就好理解了，我们首先减去(1,1)到(i,l-1)区间的数值和，在减去(1,1)到(k-1,j)的数值和 由于它们的交叉重叠部分Val[k-1][l-1]被我们减去了两次，所以最后我们加上这个值就好了。那我们如何创建一个前缀和数组Val[i][j]呢？首先，我们先读入当前(i,j)位置的值，然后再让，Val[i][j]+=Val[i][j-1]+Val[i-1][j]-Val[i-1][j-1] 所以说，为了防止数组越界和保证正确的计算读入，我们最好从i=1,j=1开始读入数据。

完成准备工作以后，再来审视一下这个题目，可以发现，我们要让棋盘剩下n块，就必须切割棋盘n-1次，那问题就来了，我们如何去思考这一过程的dp数组的更新和决策？又如何把它和一大堆子问题联系在一起呢？其实，第一刀切割的位置是有限的（横着切，m行有m-1种切法，竖着切，p行有p-1种切法），所以说，我们枚举第一刀切割的位置即可，切下的这一大块就是n块中的一块，所以设定一个函数f(i,j,k,l,num)表示切割(i,j)到(k,l)位置，使得棋盘变成num块的最小平方和值。边界条件就是num=1的时候，这个时候直接返回棋盘的平方和的值就好了，所以一个记忆搜索法的程序就出来了。

代码实现1

#include <iostream>
using namespace std;int n,board[9][9]={0};
int dp[10][10][10][10][16]={0};int V(int k,int l,int i,int j){return board[i][j]-board[i][l-1]-board[k-1][j]+board[k-1][l-1];
}int S(int x){return x*x;
}int f(int i,int j,int k,int l,int p){if(p==1){return S(V(i,j,k,l));}if(dp[i][j][k][l][p]) return dp[i][j][k][l][p];int ans=1e9,val1,val2;for(int m=j;m<l;m++){val1=f(i,j,k,m,1)+f(i,m+1,k,l,p-1);val2=f(i,j,k,m,p-1)+f(i,m+1,k,l,1);ans=min(ans,min(val1,val2));}for(int m=i;m<k;m++){val1=f(i,j,m,l,1)+f(m+1,j,k,l,p-1);val2=f(i,j,m,l,p-1)+f(m+1,j,k,l,1);ans=min(ans,min(val1,val2));}dp[i][j][k][l][p]=ans;return ans;
}int main(){scanf("%d",&n);for(int i=1;i<=8;i++){for(int j=1;j<=8;j++){scanf("%d",&board[i][j]);board[i][j] += board[i-1][j] + board[i][j-1] - board[i-1][j-1];}}int result=f(1,1,8,8,n);printf("%d\n",result);return 0;
}

当然啦，直接用for循环打表也是一个很好的选择，而且不太容易爆栈空间。

首先，程序使用一个二维数组val来存储棋盘格子的分值，并使用前缀和的方式计算出每个格子左上方区域的分值和。这样可以在后续计算中快速获取任意矩形棋盘的总分。

然后，程序使用一个五维数组dp来动态规划地计算平方和的最小值。数组dp[t][k][l][i][j]表示将棋盘分割为t块矩形棋盘时，在区域(k,l)到(i,j)之间的平方和的最小值。

接下来，程序使用嵌套的循环遍历所有可能的矩形棋盘区域，并计算出对应的平方和。初始状态下，当t=1时，直接计算出每个矩形棋盘的平方和。

然后，程序通过动态规划的方式计算出将棋盘分割为t块矩形棋盘时的最小平方和。对于每个t，通过遍历所有可能的切割位置，将棋盘切割为两个子区域，然后使用之前计算得到的结果dp[1][k][l][i][c]和dp[t-1][k][c+1][i][j]（或dp[t-1][k][l][i][c]和dp[1][k][c+1][i][j]）计算出当前状态的最小平方和。通过遍历所有切割位置，找到最小的平方和，并将结果存储在dp[t][k][l][i][j]中。

最后，程序输出dp[n][1][1][8][8]，即将整个棋盘分割为n块矩形棋盘时的最小平方和。

这种动态规划的解决方法可以有效地解决棋盘分割问题，并找到平方和的最小值。

代码实现2

#include <iostream>
using namespace std;int val[9][9],n,dp[16][10][10][10][10]={0};int V(int k,int l,int i,int j){return val[i][j]-val[i][l-1]-val[k-1][j]+val[k-1][l-1];
}int S(int x){return x*x;
}int main(){scanf("%d",&n);for(int i=1;i<=8;i++)for(int j=1;j<=8;j++){scanf("%d",&val[i][j]);val[i][j]+=val[i-1][j]+val[i][j-1]-val[i-1][j-1];}for(int i=1;i<=8;i++)for(int j=1;j<=8;j++)for(int k=i;k<=8;k++)for(int l=j;l<=8;l++){dp[1][i][j][k][l]=S(V(i,j,k,l));}for(int t=2;t<=n;t++)for(int k=1;k<=8;k++)for(int l=1;l<=8;l++)for(int i=k;i<=8;i++)for(int j=l;j<=8;j++){int ans=1e9;for(int c=l;c<j;c++){int val1=dp[1][k][l][i][c]+dp[t-1][k][c+1][i][j];int val2=dp[t-1][k][l][i][c]+dp[1][k][c+1][i][j];ans=min(ans,min(val1,val2));}for(int c=k;c<i;c++){int val1=dp[1][k][l][c][j]+dp[t-1][c+1][l][i][j];int val2=dp[t-1][k][l][c][j]+dp[1][c+1][l][i][j];ans=min(ans,min(val1,val2));}dp[t][k][l][i][j]=ans;}printf("%d\n",dp[n][1][1][8][8]);return 0;
}