B2
非对称加密介绍
前面的传统加密算法都是对称加密。就是加密解密用一个密钥。非对称加密就是用不同的密钥,加密复杂度更高。
Diffie-Hellman 密钥交换法
一种密钥交换方法。
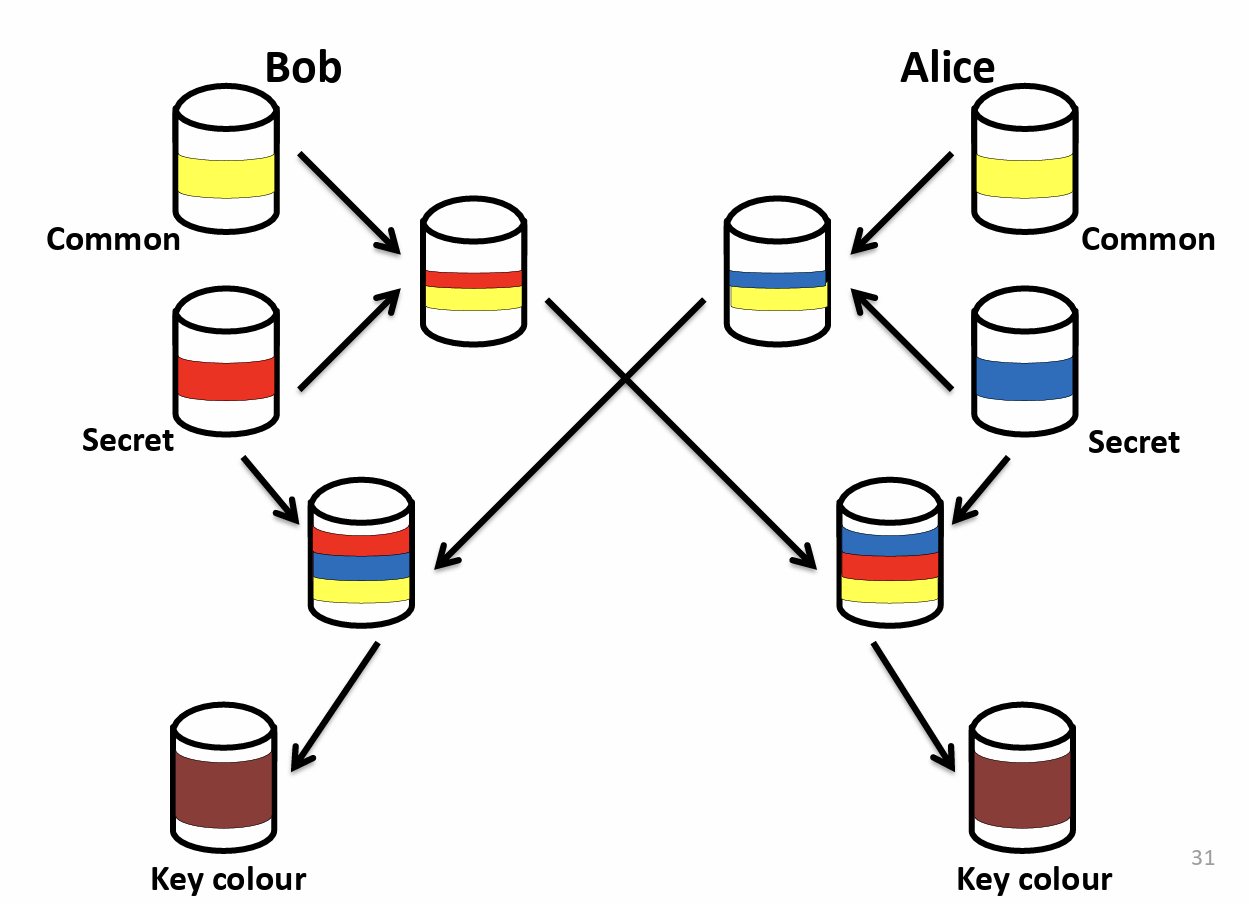
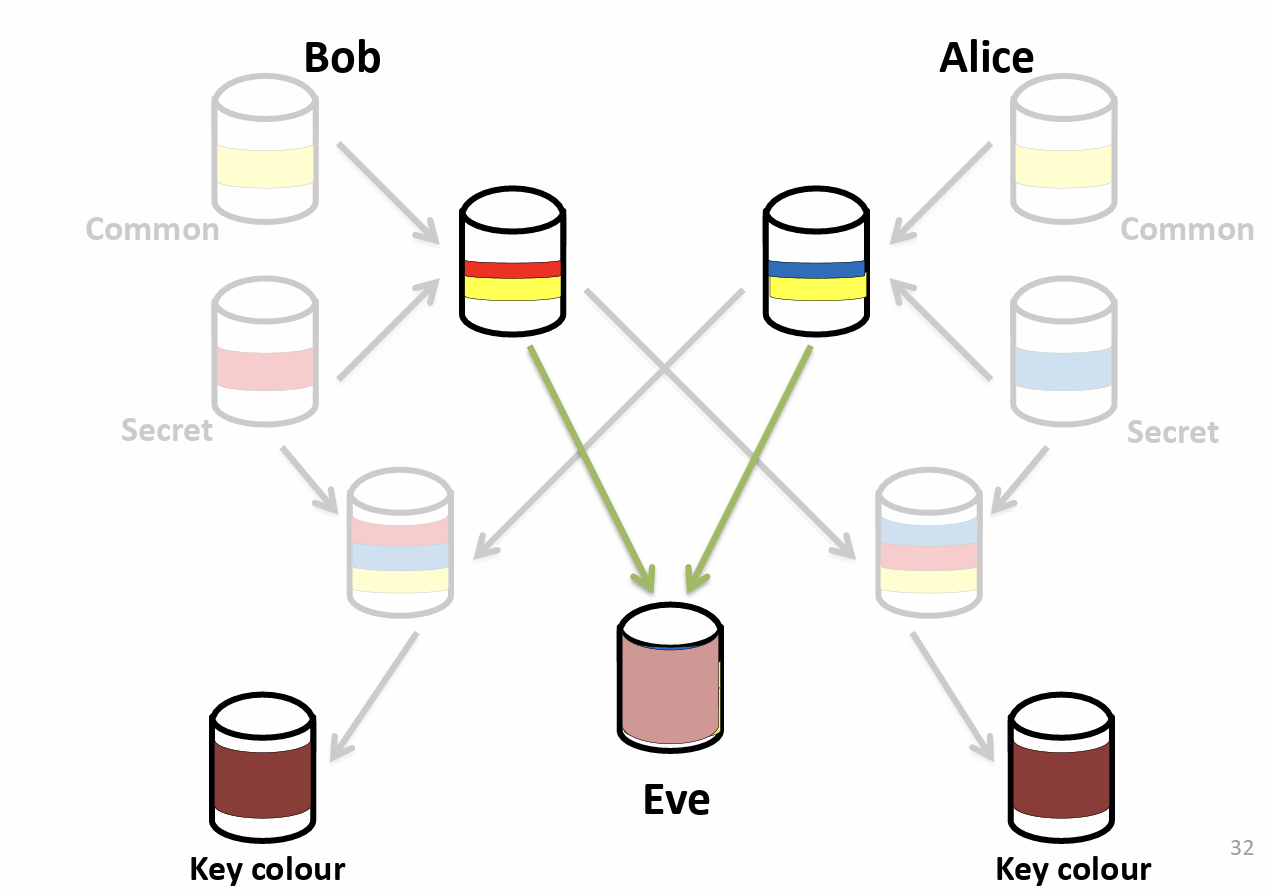
common 是公共基础颜色,secret 是各自私有颜色,公共颜色和自己的私有颜色混合后给对方,对方再和自己的私有颜色混合,两者就都得到了一个共同的秘密颜色。中间被别人截到别人也不会知道密钥颜色是什么,他拿到的是橙色和绿色。哪怕他把这两种颜色混合,也得不到一样的棕色。
Diffie-Hellman 具体实现是通过原始根来实现的,我们先补充一点知识。
数论里学过,很简单的东西。比如 13 mod 12 =1.
原始根 primitive root:如果

那么 a 就是 p 的一个原始根。
比如下图,7是71的原始根,8不是,出现了重复。

对于 Diffie-Hellman,黄色颜色(common)包括 a 和 p。a 是 p 的一个原始根。
Alice 的红色秘密颜色为 x,Bob 的蓝色秘密颜色为 y。
ax mod p 是 Alice 发给 Bob 的混合颜色信息,ay mod p 是 Bob 发给 Alice 的。两者拿到后再做一下取模运算。
证明(q)n mod p = qn mod p 的证明如下:DH算法图解+数学证明-CSDN博客
反正根据上式,我们可知,(ax mod p)y mod p = (ay mod p)x mod p = axy mod p,两者得到的都是棕色的最终颜色。
破解方法:中间人攻击,与两边分别达成一项 DH 密钥协议,然后收发消息的时候分别使用双方的密钥协议加密解密,Alice Bob 都没有收到真正的对方的密钥信息。
Trapdoor One-Way Function
单向陷门函数。y=f(x) 很好计算,x=f-1(y) 很难计算,如果知道 z 后计算逆函数就很方便,那么 z 就是陷门。对于 RSA 来说,私钥就是陷门 trapdoor。
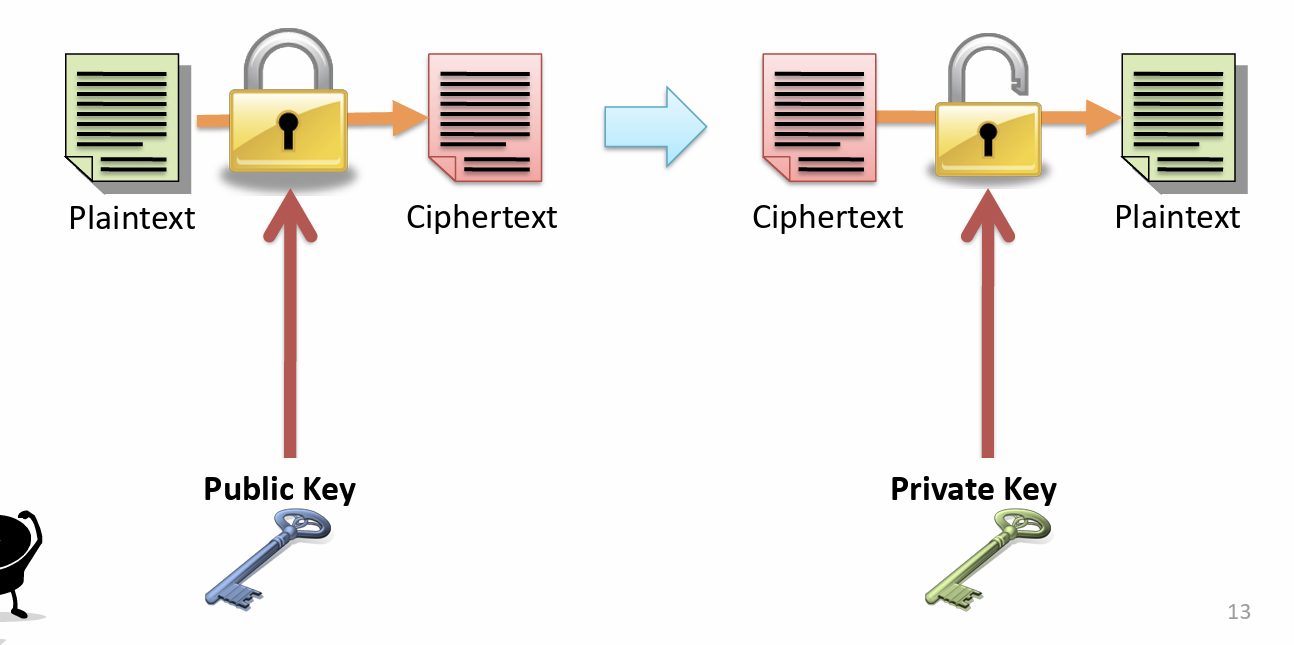
RSA 公钥加密算法
先补充一点数论知识。
互素 relative prime:两个数字没有共同因子(除了1),比如7 和 10,不一定需要两者都是素数。gcd (a, b) = 1
Φ(n):小于n的最大的和n互素的数。比如对于素数p, ϕ ( p ) = p − 1 \phi(p)=p-1 ϕ(p)=p−1 ; ϕ ( 1 ) = 1 \phi(1)=1 ϕ(1)=1
p q 互素,n=pq, ϕ ( n ) = ( p − 1 ) ( q − 1 ) \phi(n)=(p-1)(q-1) ϕ(n)=(p−1)(q−1)
n=p2 , ϕ ( n ) = ( p ) ( p − 1 ) \phi(n)=(p)(p-1) ϕ(n)=(p)(p−1)
同余:模一个数得到的余数相同,则这两个数同余。比如 1 4 对3同余。1≡4 mod 3
欧拉定理:如果 a n 互素,那么 a ϕ ( n ) ≡ 1 ( m o d n ) a^{\phi(n)}≡1 (mod \quad n) aϕ(n)≡1(modn)
RSA 算法:首先对于每次处理的明文 m,有 m<n.
然后,公钥对是 {e, n},加密方法是 c=me mod n。
私钥对是 {d, n},解密方法是 m=cd mod n=med mod n.
那么存在 ed 使得 m mod n = med mod n,而且已知 e n,d 不好找。
常用的算法是,我们使用两个大质数 pq 和给定的 e,n=p*q, ϕ ( n ) = ( p − 1 ) ( q − 1 ) \phi(n)=(p-1)(q-1) ϕ(n)=(p−1)(q−1) , d ≡ e − 1 m o d ϕ ( n ) d≡e^{-1} mod\quad \phi(n) d≡e−1modϕ(n) 或 e d ≡ 1 m o d ϕ ( n ) ed≡1 mod \quad \phi(n) ed≡1modϕ(n)
为什么这样设置 n 可以使得 med mod n=m mod n?
med mod n = m1+k(p-1)(q-1) mod n = m(mk(p-1)(q-1) ) mod n = m*1k mod n=m mod n。好像是因为 n 选取的质数非常大,所以 m n 是互质的,满足欧拉定理;如果不满足,那么也可以根据中国剩余定理证明成立,这里我就不浪费时间补充了,快考试了 qaq。
破解方法:暴力破解法(太慢了),根据素数的一些特性的数学破解法,定时攻击(根据输入输出运算时长判断密钥信息),选择密文攻击(根据 rsa 的特性可以解出一些明文密文对,比如 c1*c2 mod n 就是 m1 * m2 的加密结果。
公钥加密的缺陷:需要密钥长度太大,计算太慢,而且如果长度过长需要 ECB 分块加密,这种方法并不可取,缺少一个分块处理的方法。
Hybrid Encryption 混合加密
结合高效的对称加密和复杂的对称加密。传输大数据量的时候使用。
假定双方有非对称加密密钥,用非对称方式传输对称密钥(session)。然后双方使用对称密钥通信。
Certificates 证书
加密:对方公钥加密,对方用自己的私钥解密。
加签名,确保消息是自己发的:用自己的私钥加密,对方用公钥解密。
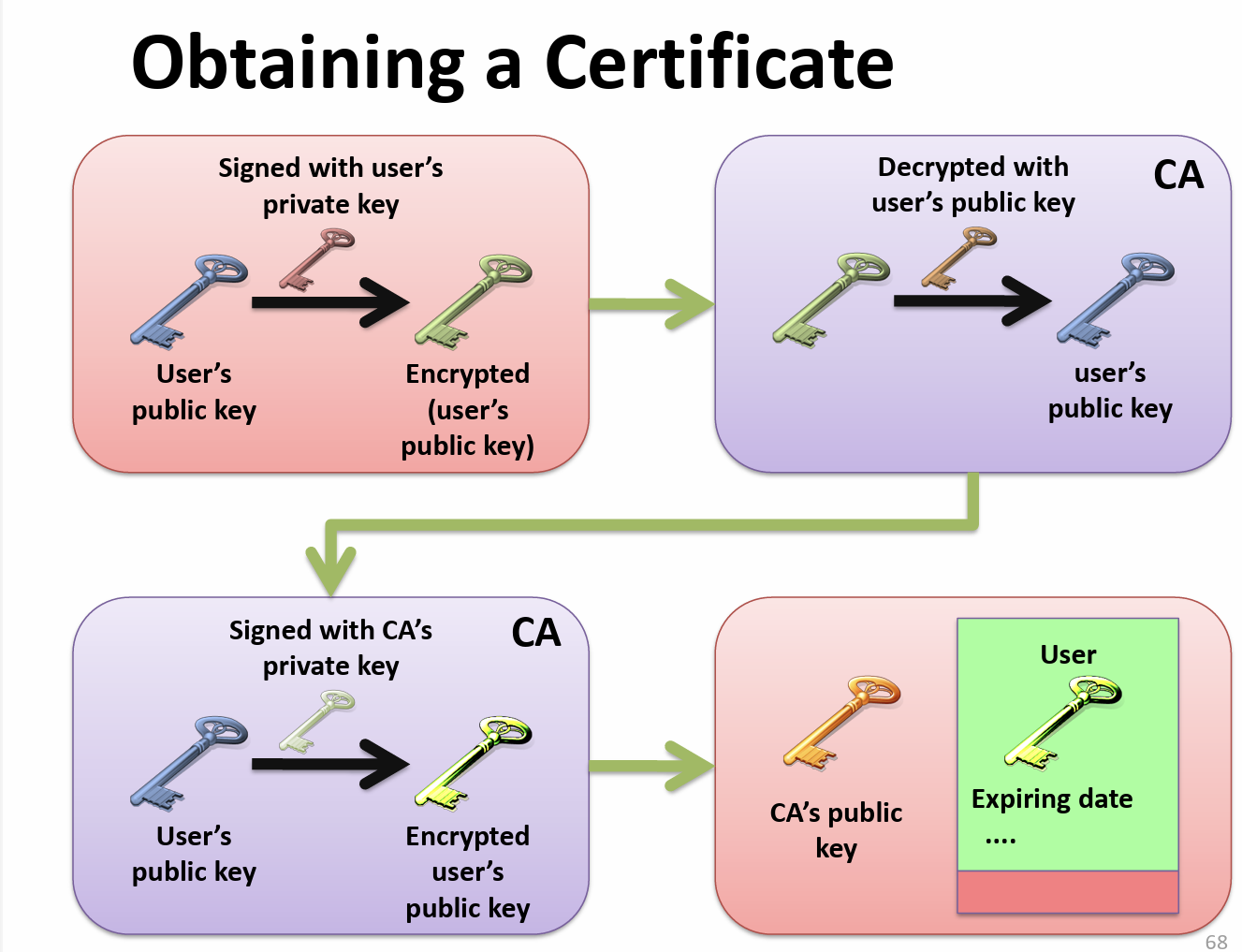
Alice 用自己的私钥加密后,CA 证书授权机构有办法校验签名是否是 Alice 发出的(CA 不用存储私钥信息,就可以有办法校验签名的作者)。CA 自己的私钥加密也可以被其他人校验签名。
发信息流程:Alice 签名 -> CA 认证是 Alice 的信息 -> CA 签名 -> Alice 认证 CA 的签名 -> CA 或 Alice 发送信息给 Bob。
Authentication 授权
数据完整性:数据没有被未授权的方式修改。也就是说篡改数据,或者有个中间人自己伪造了一份数据这些都能被检测出来,不能纠错但是可以检错。
这里有一个很有意思的误区,保密性和真实性的问题。授权只是确保真实性。
如果用传统加密方法,确保 data integrity 的方法如下:
- 保证只有收发双方得到信息。
- 用时间戳核实。
- 用检错序列号核实。
不过传统加密没法通过签名核实身份,也就是说中间人可以自己伪造信息。
而且加密方法来认证授权并不合适,计算量大,不如信息加一个 授权 tag 进行广播,而且现在很多计算机程序自带校验授权方法不用加密实现。
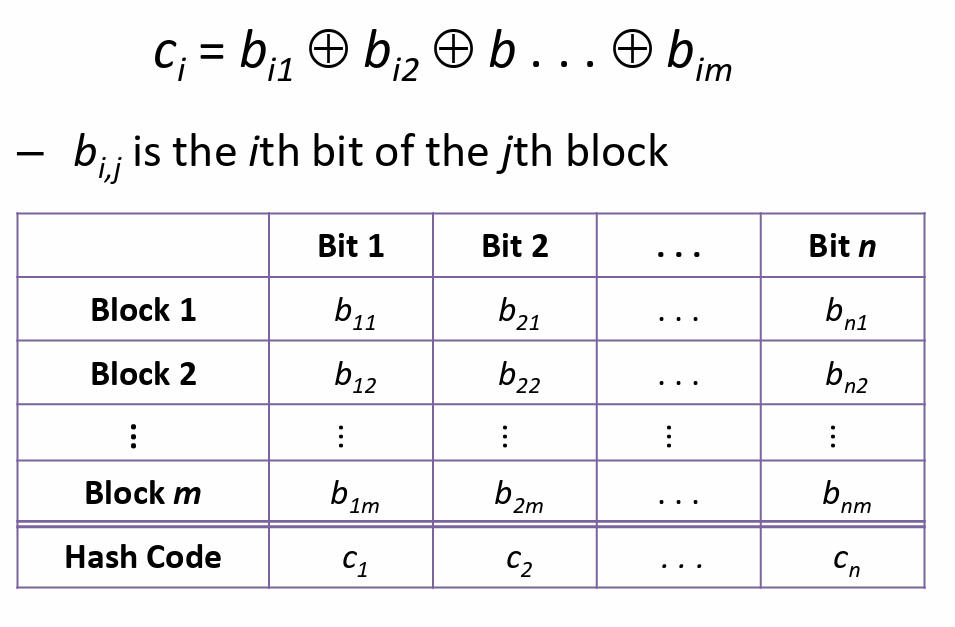
Longitudinal redundancy check (LRC) 纵向冗余校验
每个块的第i位拿出来异或一下得到校验码。随机数据很合适,但是对可预测的格式化数据不太合适。
Hash functions
输入永远得到固定长度的输出,算法公开,输入容易计算输出,输出很难反过来计算输入。
-
Preimage Resistance:给定h(m)=c,很难根据这个c找到m。可以用于数据库保存用户密码,数据库管理员看到c不知道原密码是啥。
-
Second Preimage Resistance:给定 m 和 h(m),很难找到n≠m且h(m)=h(n)。下载软件后计算哈希值核实软件完整性。
-
Collision Resistance:对于哈希函数h,很难出现n≠m且h(m)=h(n)。比如 bob 给 alice 发消息说借我100,alice 在这条消息的 hash 上签名了;但是如果 bob 找到了另一条消息:借你100000元,也和"借你100元"有一样的 hash 值,那他可以说其实 alice 答应借我 100000。要避免这种事情发生。
这样发送方发送自己的消息和消息的哈希值,接收方就可以校验完整性(保密性没法校验)了。
还可以用于生成伪随机数。
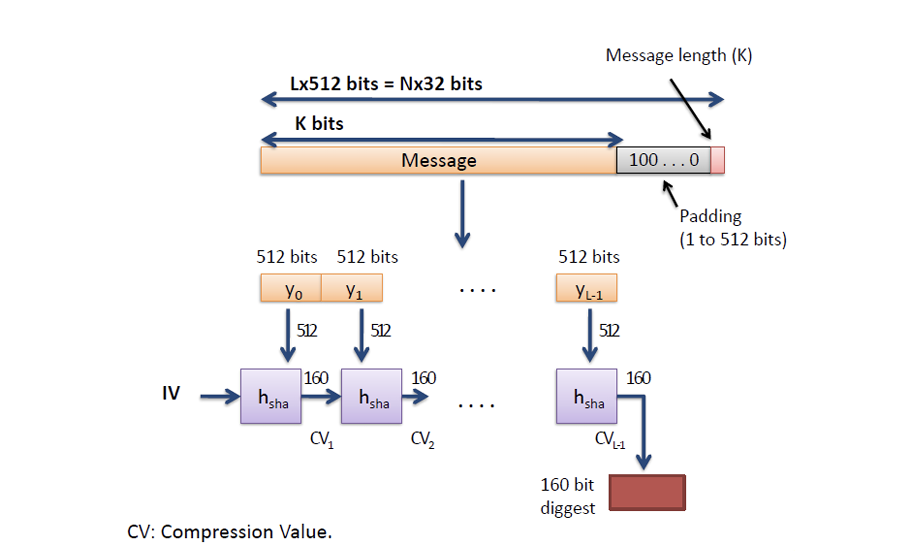
比如 SHA1:简单说就是先扩展到512位的整数倍,然后每次拿512位出来处理一次,不断迭代最后得到一个512位的哈希值。
破解办法就是暴力破解或密码分析。
Preimage Resistance & second Preimage Resistance:平均需要尝试 2m-1 次。
Collision Resistance:2m/2 代表 Collision Resistance 的强度(碰撞可能性)。生成的哈希值当然越长越小可能碰撞。
生日攻击
birthday attack。如果我们想让一群人里面至少有两个同一天生日,应该选多少人?令人非常吃惊的是70个人就能达到90%的概率(会发生生日重复)了。
所以哈希值的问题我们也不需要尝试几乎所有组合。比如对于64位消息,创建232 个消息变体很大概率上就能出现重合的哈希值了。
MAC
也是一种 散列算法,消息和密钥一起算散列值,然后附着在消息上发给对方。对方知道密钥的情况下,计算消息+密钥看 mac 值是否一样,不一样就说明消息变过或者发送人不对。
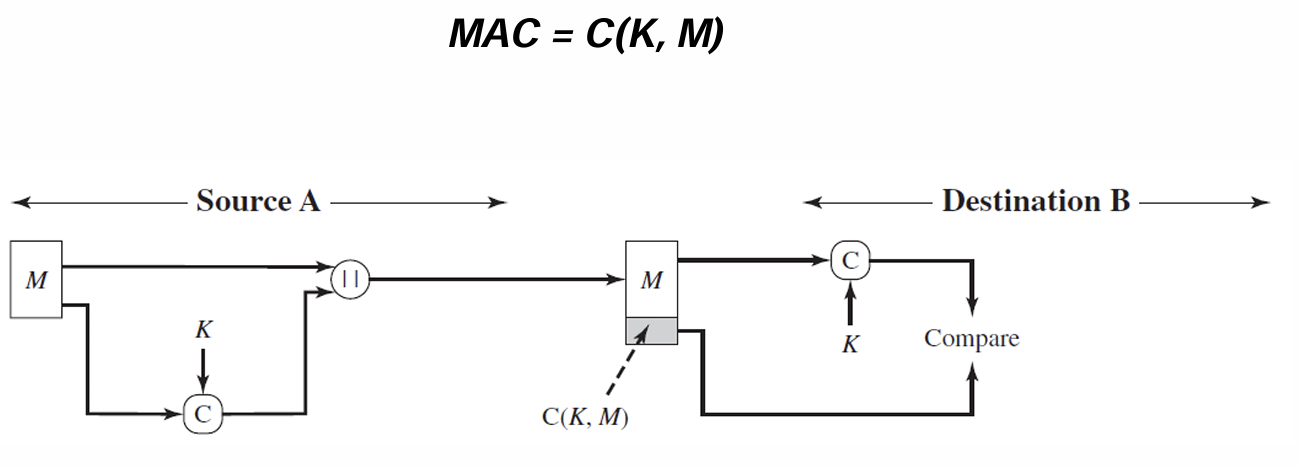
和单向函数相比,单向函数只能确保数据完整性,mac 还能 authentication(因为密钥只有自己和对方知道,所以 mac 对上了也能说明发送信息的人确实是和自己共享密钥的对方)。
HMAC
MAC 基于多种加密方式,hmac 是专于 hash 的。并且 HMAC 很方便更换散列函数,只需要删除(remove)有的散列函数模块并插入(drop in)新的即可。
数字签名
用于:
- 确保数据完整性和签名者的授权身份。
- 不可抵赖性 Non-repudiation,签名者无法抵赖自己发的数据。
实现上感觉类似 MAC,数据信息+secret 参数信息,通过哈希算法得到签名。