少年们,大家好。我是博主
那一脸阳光,今天和分享数组交换和二分查找。
前言:探索C语言中的数组交换操作与二分查找算法在计算机编程领域,特别是以C语言为代表的低级编程语言中,对数据结构的理解和熟练运用是至关重要的。数组作为最基本的数据结构之一,在C语言中被广泛应用,它允许我们一次性存储和管理相同类型的一系列数据元素。
数组交换操作是数组处理中常见的基本操作之一,常用于排序算法、冒泡排序、选择排序等过程中,通过交换数组中两个指定位置的元素来达到改变数组元素顺序的目的。在C语言中,交换数组元素通常需要借助一个临时变量来实现,这既体现了程序设计的灵活性,也展示了指针操作的精妙之处。
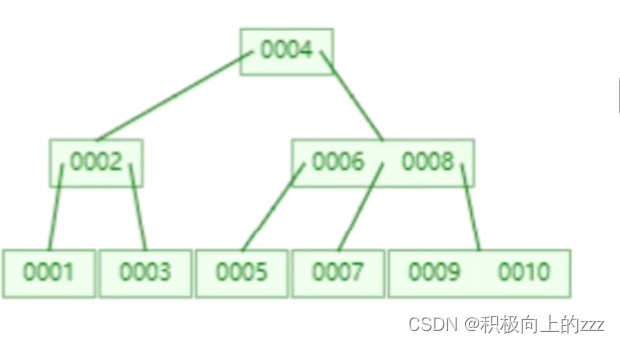
另一方面,二分查找算法是一种基于有序数组的高效搜索算法。其核心思想是在有序数组中,每次通过比较中间元素将待查找区间缩小一半,直至找到目标值或确定目标不存在于数组中。在C语言中实现二分查找,不仅能够提升代码的运行效率,而且能帮助我们深入理解递归和循环等控制结构的应用,以及如何有效利用数组的有序特性进行问题求解。
综上所述,掌握C语言中数组交换操作以及二分查找算法,不仅有助于日常编程实践,也有利于提高逻辑思维和问题解决能力。接下来,我们将详细介绍这两种操作的具体实现方式和应用场景。
我来分享一道题,交换两个数组,然后打印出来。
数组内容:
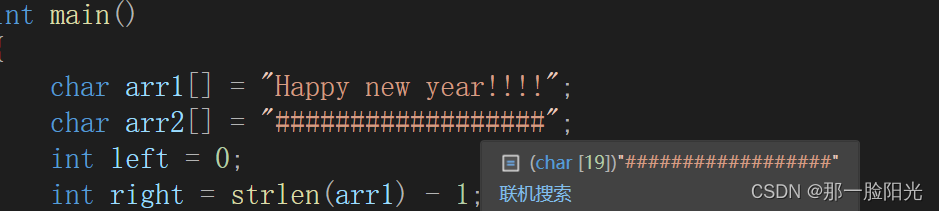
第一个数组Happy new year!!!!
第二个数组 "##################";
```交换两个数组内容> 这是个思维导图,我们我把这个给规划一下,从而使得这个问题变得简单明了。
>
> **>第一步创建两个数组;```c> char array1[]={"Happy new year!!!!"};
> char array2[]={"###################"};

这时候我们需要计算交换次数,那交换多少次呢?我们再来规划一下这个问题。
可以看到他们元素大小都是一样的才能交换,负责没写的部分因为没有斜杠,会出现乱码,
所以得出结论,他们数组元素的内容是一样多的。我们想要访问某个元素的时候就需要使用到下标,一个元素的下标是【0】,好我们确定一个元素的下标,那我们找到最后一个元素的下标是,数组元素所有的内容减1,就是下标。
int left=0;
int right=strlen(arr1)-1;
这里left是数组第一个元素的下标,strlen计算出的是数组元素的大小所以减1就是数组下标。
那接下来我们该如何访问数组下标呢?那介绍一下遍历数组
在C语言编程中,数组是最基础且广泛使用的数据结构之一。它允许我们将相同类型的数据元素存储在一起,并通过索引进行访问。本篇将详细介绍如何在C语言中遍历数组,包括常见的遍历方法以及相关示例。
在C语言中,遍历数组通常指的是访问数组中的每一个元素。以下是一些常用的遍历数组的方法:
- 使用for循环遍历数组
. // 假设有一个整数数组arr,长度为n
int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int n = sizeof(arr) / sizeof(arr[0]); // 获取数组元素个数for (int i = 0; i < n; ++i) {printf("数组的第 %d 个元素是: %d\n", i + 1, arr[i]);
}
int arr[10] = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10};
int i = 0;
int n = sizeof(arr) / sizeof(arr[0]);while (i < n) {printf("数组的第 %d 个元素是: %d\n", i + 1, arr[i]);++i;
}
好大家有所理解遍历数组了,那我们把这道题解决一下吧
char arr1[] = "Happy new year!!!!";char arr2[] = "##################";int left = 0;int right = strlen(arr1) - 1;```while(left <= right){arr2[left] = arr1[left];arr2[right] = arr1[right];left++;right--;printf("%s\n", arr2);}return 0;}这段代码通过遍历数组,访问数组元素实行交换,大家应该已经能有所理解了吧。好我们下篇来分享二分查找。