PyTorch 节省显存技巧：Activation Checkpointing-编程知识

参考资料

官方文档： https://pytorch.org/docs/2.0/checkpoint.html
官方博客：https://medium.com/pytorch/how-activation-checkpointing-enables-scaling-up-training-deep-learning-models-7a93ae01ff2d

Activation Checkpointing 介绍

激活检查点 (Activation Checkpointing) 是一种用于减小内存占用的技术，代价是需要更多的计算资源。它利用一个简单的观察，即如果我们只是在需要时重新计算反向传播所需的中间张量，就可以避免保存这些中间张量。

目前在 PyTorch 中有两种 Activation Checkpointing 的实现，即可重新进入 (reentrant) 和不可重新进入(non-reentrant)。不可重新进入版本是后来实现的，以解决可重新进入检查点的一些限制，这些限制在 PyTorch 的官方文档中有详细说明。可以通过传递 use_reentrant 标志来指定使用哪个版本的检查点。目前，use_reentrant 标志是可选的，可重新进入版本是默认的。然而，在 2.1 版本中，不明确传递该标志将被弃用。在 PyTorch 的将来版本中，不可重新进入版本将成为默认值。

在本文中，我们首先提供一些关于 PyTorch 自动求导如何工作的一般背景。然后，我们探讨了激活检查点的新的不可重新进入实现，并将其与早期的可重新进入实现进行了比较。所呈现的实现将被简化以便于读者理解。

PyTorch 中的自动求导

在我们深入讨论之前，让我们简要回顾一些后续需要的概念。

PyTorch 用于存储和操作数据的基本构建块是张量（tensor）。默认情况下，张量与带有 GPU 支持的 NumPy 数组没有太大区别。当一个张量的 .requires_grad 属性被设置为 True 时，自动求导引擎就会启动。

然后对张量应用的每个变换都会创建一个特殊的对象，该对象除了包含生成的张量外，还知道如何计算反向传播的转换。可以通过结果张量的 .grad_fn 属性访问该对象。

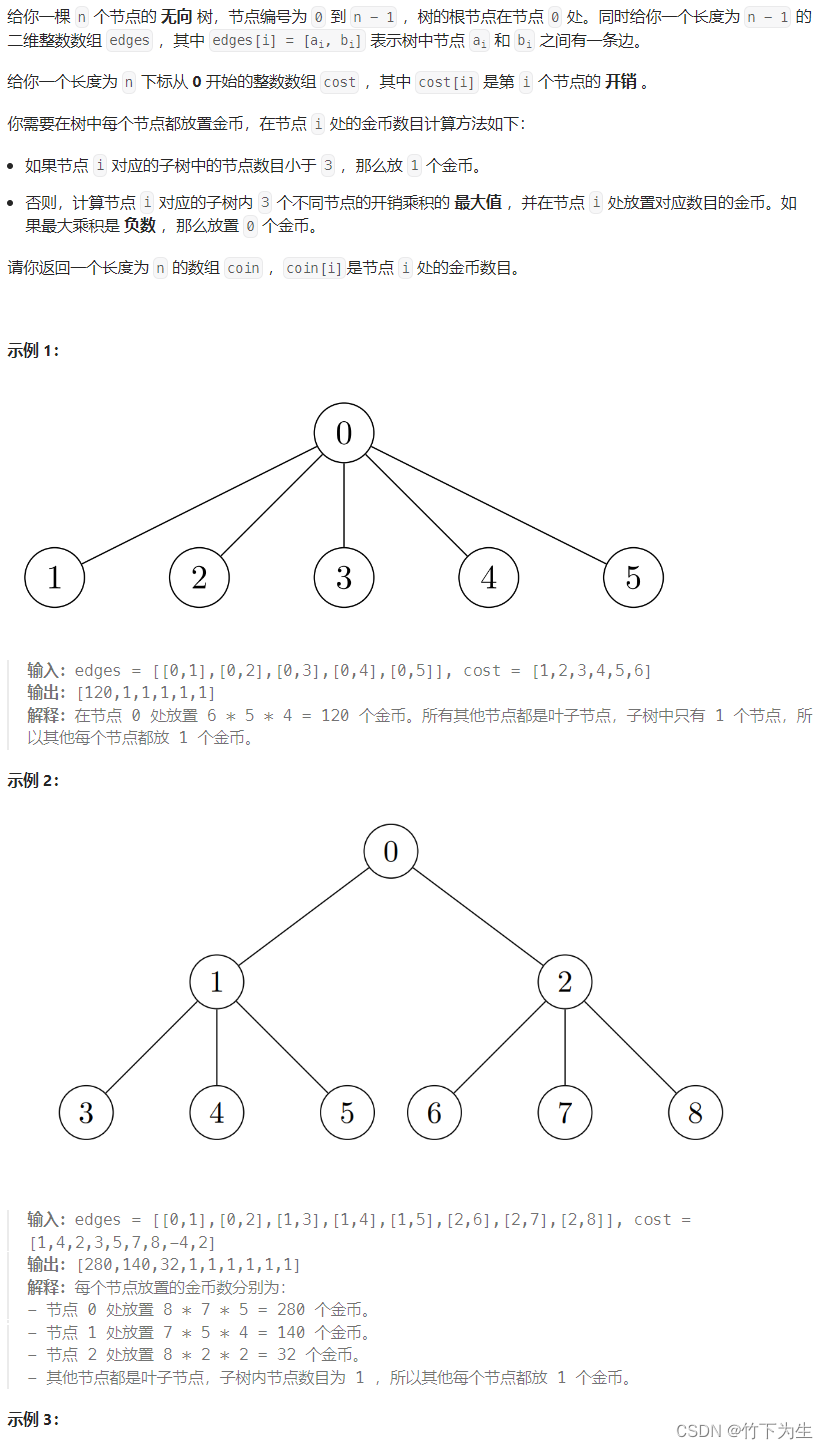
同样的对象还连接到其他类似的对象，所有这些对象都作为有向无环图（DAG）中的节点，称为计算图。当创建一个新节点时，自动求导通过使其 .next_functions 属性指向创建它的现有节点，将其添加到图中。

让我们关注一个具体的例子。在以下代码片段中：

a = torch.tensor([2.], requires_grad=True)
b = torch.tensor([3.], requires_grad=True)
c = a + b
d = c.sin()

c 和 d 分别对应于加法和正弦函数的反向传播的节点。

a 和 b 是直接创建而不是作为操作的一部分创建的张量，被称为叶子张量。

这样的节点具有一个特殊的 AccumulateGrad 节点，该节点具有一个指向它们张量的 .variable 属性。

一个有帮助的思考方式是将它们视为两个层次 - 一个用于张量，一个用于构建计算图的反向函数。一个层次（图中的底部）由不相互连接的张量组成，但可以通过 .grad_fn 属性连接到反向函数；另一个层次（图中的顶部）用于反向函数，这些函数不知道张量 - 除了 AccumulateGrad 特殊函数外 - 并使用 .next_functions 属性连接。

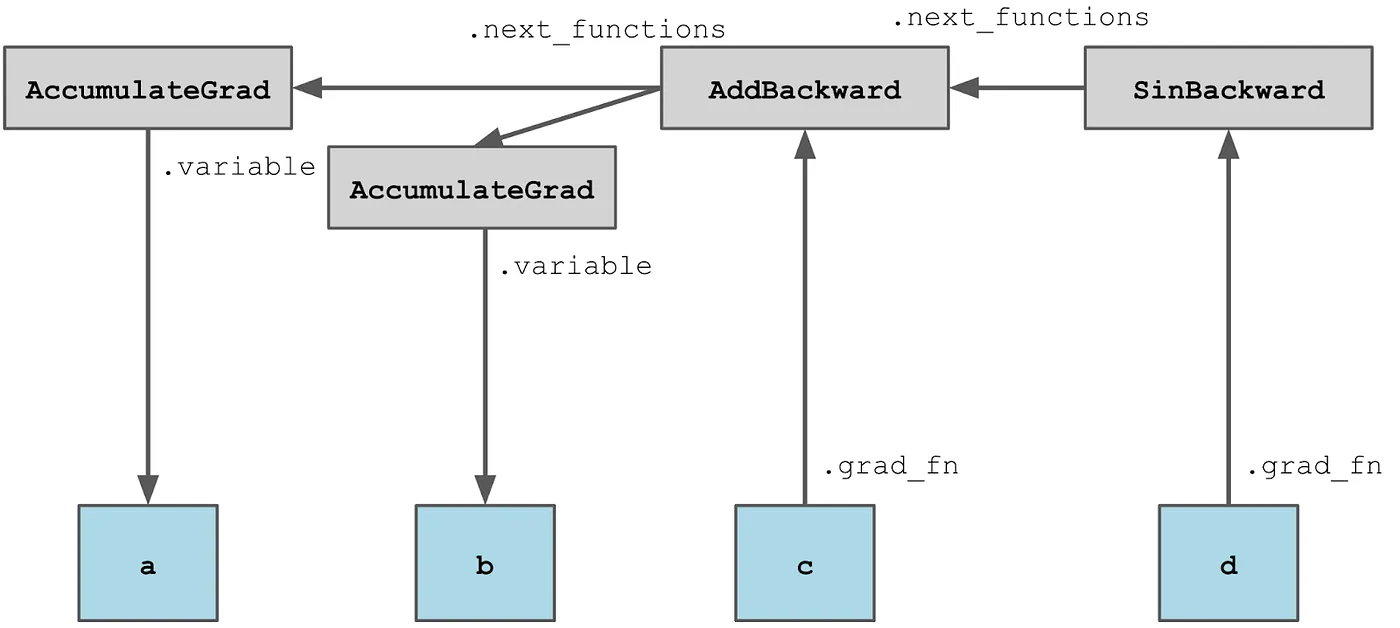
在这里插入图片描述

对具有 requires_grad 的张量执行的每个操作都会在计算图中创建一个新节点，这种行为可以在 torch.no_grad() 上下文管理器中禁用，并在内部的 torch.enable_grad() 上下文管理器中重新启用。

然而，并不是张量类的所有函数都会在计算图中创建节点 - 例如，torch.detach() 复制没有 .grad_fn 的张量，作为一个与任何计算图断开连接的新张量。

torch.nn 包中的更高级模块，如 Linear 和 MultiheadAttention，在计算图中并不直接参与。相反，当它们被调用时，它们只是添加了它们由低级节点组成的图。

例如，考虑一个 Linear 块，它由多个操作组成，包括与权重张量的矩阵乘法和与偏置张量的加法：

x = torch.tensor([2.])
fc = nn.Linear(1, 1)
y = fc(x)

为了简化，将临时中间张量分组，这是它在内部的样子：
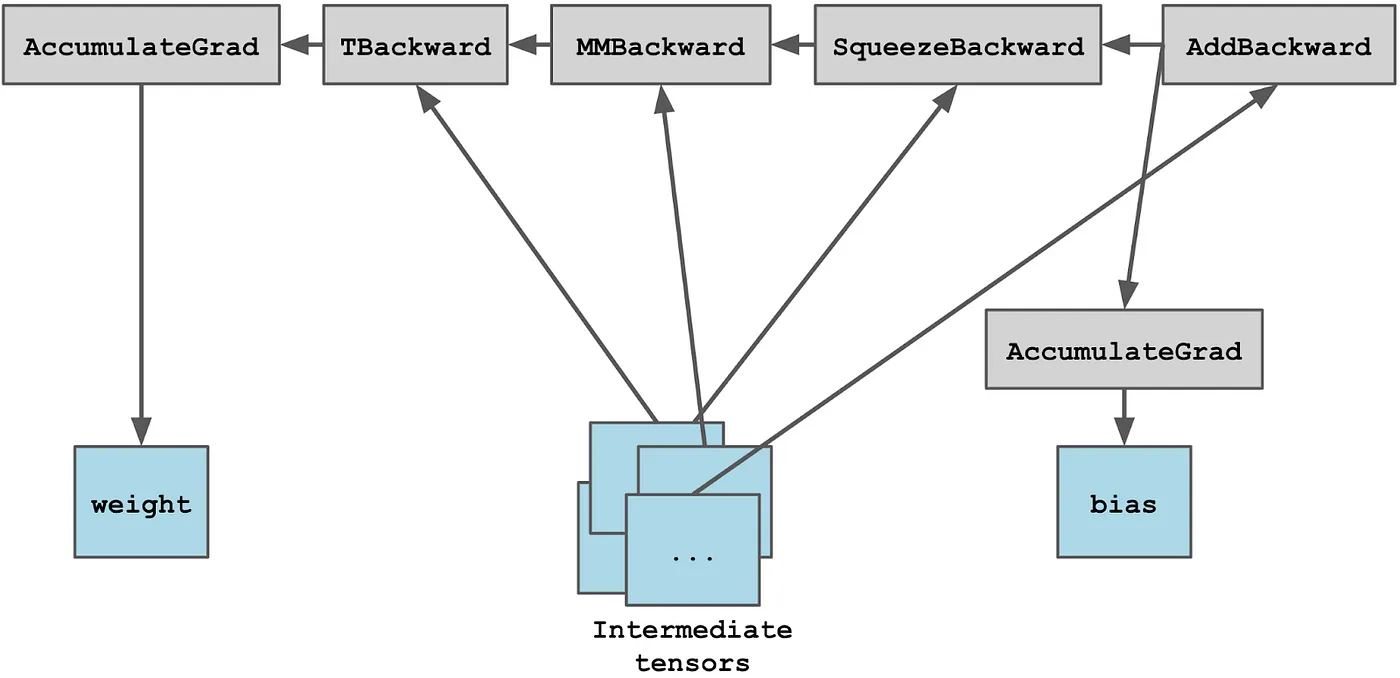
在这里插入图片描述

一旦构建了计算图，对 tensor.backward() 的调用 - 实际上是调用 torch.autograd.backward() - 将递归地计算梯度，直到存储了 .grad 的叶子节点。当这个过程停止时，计算图的角色结束并被丢弃（除非指定了 retain_graph=True）。

基于钩子的非可重入变体

激活检查点的非可重入变体利用了autograd的保存变量钩子机制。

以下是如何使用钩子的简单示例：

storage = []def pack(x):storage.append(x)return len(storage) - 1def unpack(x):return storage[x]x = torch.randn(1024, requires_grad=True)
with torch.autograd.graph.saved_tensors_hooks(pack, unpack):y = torch.square(x)
y.sum().backward()

在幕后，square 操作符保存了其输入以进行反向计算（因为 f(x) = x² 的导数是 2*x）。在这里，我们不是保存“大”张量，而是只存储其在图中的（轻量级）索引，并在以后使用该索引进行重构。尽管在这个简单的示例中实际张量也被存储了（因此没有节省空间），但这将成为激活检查点的实际非可重入版本的基础。

有了这个理解，让我们来探讨基于保存张量钩子的激活检查点的非可重入实现。为了清晰起见，它已经被简化，但整体结构保持不变：

class Frame:  # 用于共享变量的结构def __init__(self):self.recomputed = []self.count = 0class RecomputationHook(torch.autograd.graph.saved_tensors_hooks):def __init__(self, frame):def pack(x):frame.recomputed.append(x.detach())return x.detach()def unpack(X):  # 仅适用于更复杂的场景return xsuper().__init__(pack, unpack)class CheckpointHook(torch.autograd.graph.saved_tensors_hooks):def __init__(self, frame, run_function, args):def pack(unused_x): i = frame.countframe.count += 1return idef unpack(i):if not frame.recomputed:  # 仅一次，在反向传播期间解包第一个张量时with RecomputationHook(frame), torch.autograd.enable_grad():run_function(*args)res = frame.recomputed[i]frame.recomputed[i] = Nonereturn ressuper().__init__(pack, unpack)def checkpoint_without_reentrant(run_function, *args):with CheckpointHook(Frame(), run_function, args):res = run_function(*args)return res

在调用非可重入激活检查点时，函数的前向传递在 CheckpointHook 上下文管理器中运行。在此上下文管理器下，为反向传递打包和保存的任何张量都会被丢弃，并替换为占位符（这里我们任意使用其索引 i）。

在反向传递期间，尝试访问和解包其保存的张量的第一个反向函数会触发使用 RecomputationHook 重新计算 forward() 函数，该钩子截取任何保存的张量以将它们存储在 recomputed 列表中（从计算图中分离以避免引用循环）。重要的是要注意整个机制依赖于在前向和反向中按相同顺序访问 recomputed 张量。为确保这一点，实际的实现还包含保存/恢复全局状态的代码（例如，保留 RNG 状态，这对于确保像 Dropout 这样的模块在对 run_function 的两次调用中产生相同的输出很重要）。

这里未显示更复杂的情况 - 在实际代码中，每个变量的张量每个图只保存一次，并且还有一种早期停止机制以最小化不必要的计算。然而，总体结构是相同的。

torch 2.1 版本新特性

以下是2.1版本中的非可重入激活检查点的一些支持的情景：

嵌套检查点：在检查点内调用另一个被检查点的函数。这个功能允许用户在内存和计算之间做出更极端的权衡，可能将理论最小值进一步降低到 O(log(n))（在非嵌套情况下是 O(sqrt(n))）：
```
def inner1(x):...def inner2(x):...def outer(x):y = checkpoint(inner1, x)z = checkpoint(inner2, y)return za = torch.ones(1, requires_grad=True)
out = checkpoint(outer, a)
out.backward()
```
在检查点内调用 .grad()/.backward() 的支持：这对于高阶梯度计算很有用。
非确定性的改进检查和更好的调试性：从 torch 2.1 版本开始，将存储和检查基本张量元数据，以帮助验证原始和重新计算的前向调用必须以完全相同的顺序保存张量用于反向。此外，如果任何非确定性检查失败，用户可以使用 debug=True 运行检查点，这可以提供在原始运行和重新计算运行期间执行的操作的跟踪，以及在调用这些操作的时间点的堆栈跟踪，以帮助用户准确定位非确定性发生的地方。
在指定 retain_graph 时的内存节省改进

有关更多信息，请参阅文档。代码内还有一些详细的注释，详细说明了处理的各种情况，可能需要查阅以获得完整的理解。这个设计文档还包含一些关于为什么做出这些选择以及支持了哪些新情景的信息。

可重入变体

早期的实现，称为可重入变体，不使用保存的变量钩子，而是使用自定义的 autograd Function，修改了计算图。

由于官方实现包含了许多细节，我们只关注一个简化的版本：

class Checkpoint(torch.autograd.Function):@staticmethoddef forward(ctx, run_function, input):ctx.run_function = run_functionctx.save_for_backward(input)with torch.no_grad():output = run_function(input)return output@staticmethoddef backward(ctx, output_grad):run_function = ctx.run_functioninput = ctx.saved_tensorsdetached_input = input.detach()detached_input.requires_grad_(input.requires_grad)with torch.enable_grad():output = run_function(detached_input)torch.autograd.backward(output, output_grad)return None, input.grad

在前向传递中，我们计算给定输入上给定 run_function 模块的输出。由于调用在 with torch.no_grad() 上下文管理器内，不会创建中间节点和反向节点 - 操作的输出直接通过 CheckpointBackward 连接到输入的反向函数。

在反向传递中，我们首先加载传递给前向传递的对象。然后，我们分离输入并重新运行前向计算，这次在 torch.enable_grad() 上下文管理器中，以允许构建一个直到输出的计算图，然后我们通过该图反向传播以更新此块内的参数。请注意，我们必须返回两个值，一个是给 run_function，另一个是给 input，但前者是 None，因为模块不是可微分张量。

值得注意的是梯度计算不再是主要计算图的一部分 - 每次都会构建一个“迷你计算图”，在其中进行实际的梯度计算，而原始图只是协调和转发梯度。

下面以图表形式展示了这些动态:
请添加图片描述

内部图不是完全独立的 - 我们确实需要将 grad_output 传递给它，并将它计算的 input.grad 返回给外部图的其余部分。但是，当前块的所有参数，隐藏在 run_function 背后，都会在该内部 backward() 调用中得到其 .grad 属性的填充。

为简化起见，我们省略了一些详细信息，例如为第二次前向传递保存/恢复全局状态，允许不同数量的参数和输出，其中不是所有都是张量。

这个实现被称为可重入变体，因为它使用了嵌套的反向传递，在 PyTorch 术语中称为“可重入反向传递”。虽然使用嵌套的反向传递可能看起来很简单，但实际上，这个实现有一些限制，例如在某些情况下无法很好地与 DDP 和 FSDP 一起使用。

用法

幸运的是，这两种设计的复杂性都包装在一个简单易用的 API 中 - 要使用的新实现是通过 use_reentrant 标志指定的，其中使用 False（即新实现）将在将来的版本中成为默认值：

from torch.utils.checkpoint import checkpointcheckpoint(run_function, args, use_reentrant=False)

总结

本文介绍了 PyTorch 中的激活检查点技术，旨在减小内存占用，同时提供更多计算资源。其中详细讨论了 PyTorch 中的自动求导机制，以及两种激活检查点的实现方式：可重新进入（reentrant）和不可重新进入（non-reentrant）。特别关注了非可重新进入版本的新特性，包括嵌套检查点、在检查点内调用 .grad()/.backward() 的支持、非确定性检查和调试性的改进、在指定 retain_graph 时的内存节省等。同时，还介绍了可重新进入变体的实现方式，并提供了简单的用法示例。