【二分答案】是分治的一种,这类问题很经典,接下来几篇文章会关于二分答案相关的文章,希望同学们可以完成10道以上的【二分答案】相关问题,以此来加深对【二分答案】这类问题的个人理解。
原公众号链接:分治第二讲:二分答案之砍树问题
一、题目
题目链接:
https://www.luogu.com.cn/problem/P1873

题意:找到一个最恰当的高度砍树,使得砍树得到的树木高度之和刚好大于等于M即可。看题目数据范围,1<=n<=10^6,通过这个数据范围,可以反推出你的算法时间复杂度只能是低于O(nlogn),因此瞬间想到二分,往二分上靠拢。
二、题目分析
题意很简单,如何求解呢?其实会发现,直接求解不是很容易求解,该问题可以归纳总结为【最小值最大问题】,即需要求解的砍树高度,在满足题目要求的情况下要最大。【最小值最大】和【最大值最小】问题均可以通过【二分答案】思路完成,在完成【二分】之前,我们先用暴力实现,然后再修改为二分即可。
对于任何一个问题,一般有两种方式解决,一种是直接求解,另一种是检验,检验指的是给一个可能解,带入题目中检查该解是否满足题目,检验类似于数学中的选择题,如果不会直接求解,那么可以依次把四个选项带入题目中检验验证即可;我个人认为:检验的难度小于直接求解。
该题目求解最恰当的砍树高度h,假设最高的那棵树的高度为maxH, 则h的取值范围为[0, maxH];可以依次让k从maxH开始依次递减直到0,递减过程中,如果某个取值恰当满足砍的树的高度之和大于等于M,则当前k就是最终解,直接输出并结束程序即可。
三、题目解决
上一部分分析了题目的求解方法并可以通过暴力的方法依次从maxH到0遍历,找到第一个满足题目要求的高度即可,试想一个问题,如果某个高度hi砍树不能满足砍掉的树的高度和大于等于M,那么对于大于等于hi的高度hj来说也无法满足题意,理解了上面这个特性就可以通过二分来快速求解高度h了。
二分的左边界left为0,右边界right为maxH,在这里扩展一个点,如果根据题意不好确定二分的初始边界left和right,那么可以直接暴力将left初始化为0,right初始化为一个很大的值,比如1e8;
Step1:取二分的中间值mid = left + (right-left)/2,检查以mid为砍树高度,是否可以得到高度大于等于M的树木;
Step2:如果不行,那么大于等于mid的高度均无法得到,因此缩小二分区间,right = mid-1;
Step3:如果可以,那么mid就是可能的一个解,保存在ans中,缩小二分区间,left = mid+1; (一定要记住,使用二分,禁止出现left = mid,因为这样很有可能陷入死循环,所以务必要避免left = mid,但是可以有right = mid);
二分问题解决了,如何实现检验函数check呢?也很简单,给你一个高度mid,遍历所有树木的高度,用sum记录砍掉的树的高度和,则如果当前树的高度小于mid,则没有得到树木,否则,在当前树上可以砍下树的高度减掉mid的差值的高度的树木,最终只需要判断sum是否大于M即可。
四、code编码
暴力代码O(n^2)
#include "iostream"
using namespace std;
const int M = 1000010;
int n, m, a[M], l = 0, r = -1, ans = -1;// check函数的功能是:给一个高度x,返回该高度是否可以砍出高度和为m的树木,如果可以返回true,否则返回false
bool check(int x) {long long sum = 0;for(int i=1; i<=n; i++) { // 遍历所有树木sum += max(0, a[i]-x); // 求解x的高度,每个树可以砍多少树木}return sum >= m; // 砍出的总和是否大于m,如果大于m则返回true,否则返回false;
} int main() {cin >> n >> m;for(int i=1; i<=n; i++) {cin >> a[i];r = max(r, a[i]); // 确定右边界,为最高的树的高度}for(int x = r; x>=l; x--) {if(check(x)) { cout << x << endl;return 0;}}}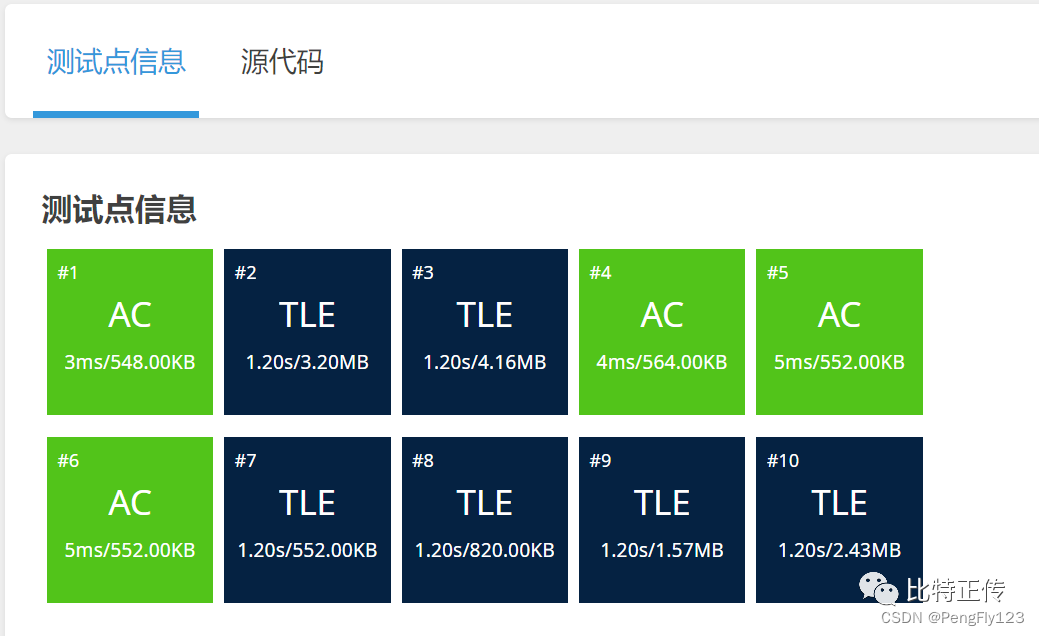
暴力超时6个点,AC了4个点,因此通过二分优化如下:
二分代码O(nlogn)
#include "iostream"
using namespace std;
const int M = 1000010;
int n, m, a[M], l = 0, r = -1, ans = -1;// check函数的功能是:给一个高度x,返回该高度是否可以砍出高度和为m的树木,如果可以返回true,否则返回false
bool check(int x) {long long sum = 0;for(int i=1; i<=n; i++) { // 遍历所有树木sum += max(0, a[i]-x); // 求解x的高度,每个树可以砍多少树木}return sum >= m; // 砍出的总和是否大于m,如果大于m则返回true,否则返回false;
} int main() {cin >> n >> m;for(int i=1; i<=n; i++) {cin >> a[i];r = max(r, a[i]); // 确定右边界,为最高的树的高度}while(l <= r) { // 二分答案int mid = l + (r-l)/2; // 找出区间的中间值if(check(mid)) { // 如果当前mid高度可以砍出m的树木高度,则说明mid是一个可能解,保存并缩小区间ans = mid; // 保存可能解l = mid + 1; // 缩小区间} else {r = mid-1; // mid高度不行,因此需要缩小右边界,答案在左区间}}cout << ans;}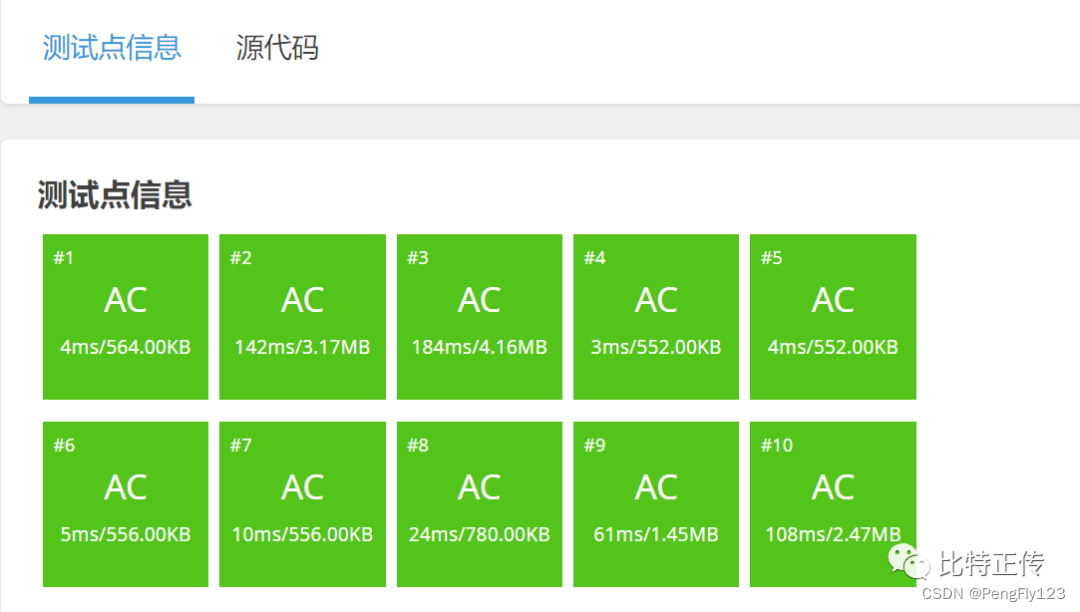
二分细节是魔鬼呀,琢磨什么时候是while(left<right),什么时候是while(left <= right)?