1 冒泡排序

1.1 冒泡排序原理

冒泡排序如同泡泡上升一样，逐个逐个向上冒，一个接一个的冒上去。两两比较，较大者（较小者）向后挪动。全部遍历一遍即可完成排序。

1.2 排序步骤

1. 首先从头开始，两两相互比较。每次排好一个最大（最小）
2. 然后在从头开始，两两比较 至已排序部分之前。
3. 依次往复，全部遍历一遍。
4. 完成排序。
   

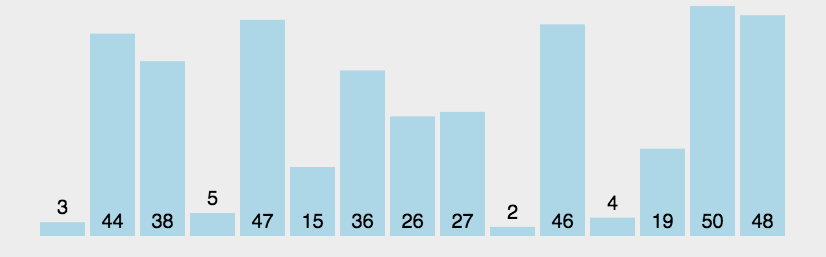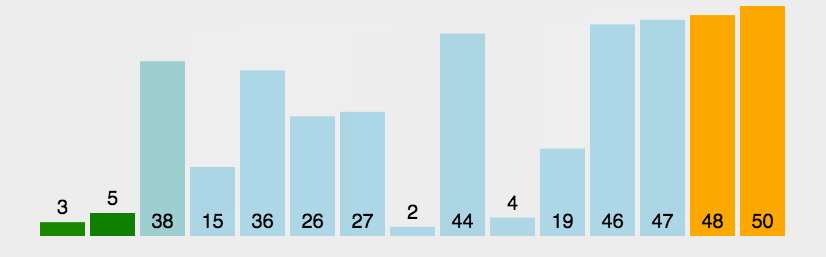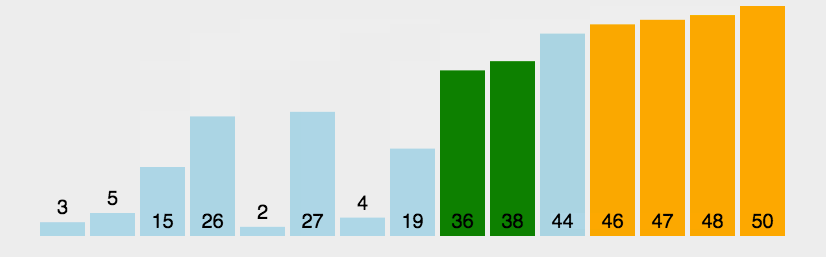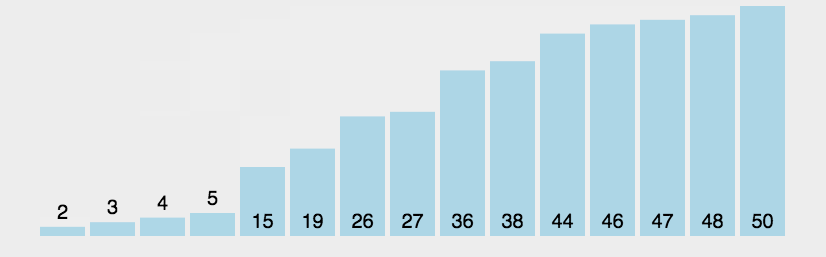
1.3 代码实现

以排升序为例

void BubbleSort(int* a, int n){for (int i = 0; i < n; i++) //从头开始遍历{//每次遍历 会排完一个 需排序部分减少 1 for (int j = 0; j < n - 1 - i;j++) {   //结束条件 a[n-2] > a[n-1]if (a[j] > a[j + 1]) //如果大，向上冒{      int tmp = a[j];a[j] = a[j + 1];a[j + 1] = tmp;}}}
}

排序结果，非常顺利。

冒泡排序的特性总结：

1. 冒泡排序是一种非常容易理解的排序
2. 时间复杂度：O(N^2)
3. 空间复杂度：O(1)
4. 稳定性：稳定

2 快速排序

2.1 快速排序原理

快速排序是一种高效快速的算法，是Hoare于1962年提出的一种二叉树结构的交换排序方法，
其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。
根据其思想 ，便有递归版本 和 非递归版本。
递归版本中有 Hoare版本， Hole版本，前后指针版本。
非递归版本使用 栈 来实现。

2.1.1 Hoare版本

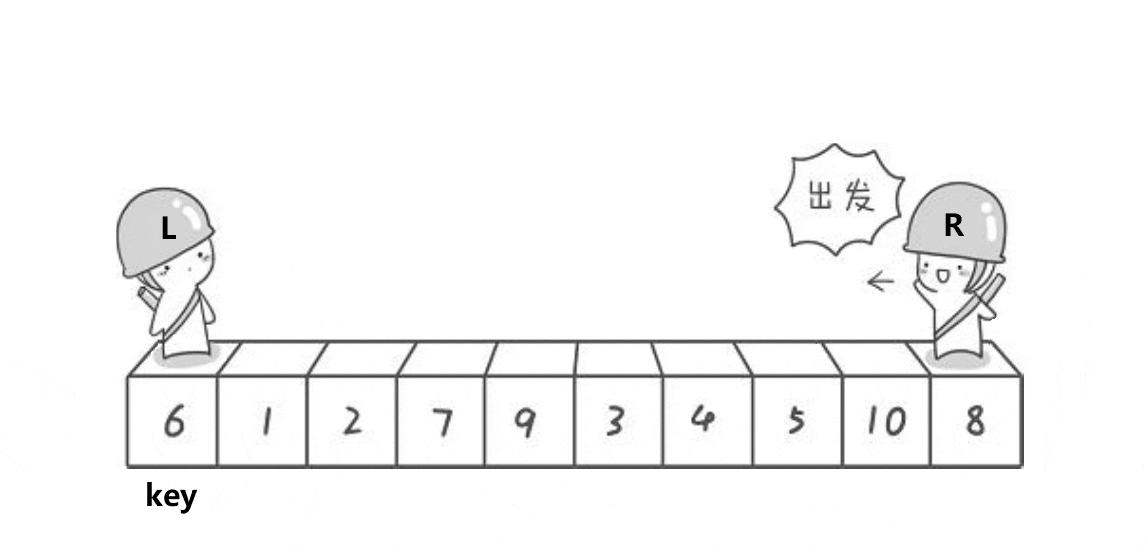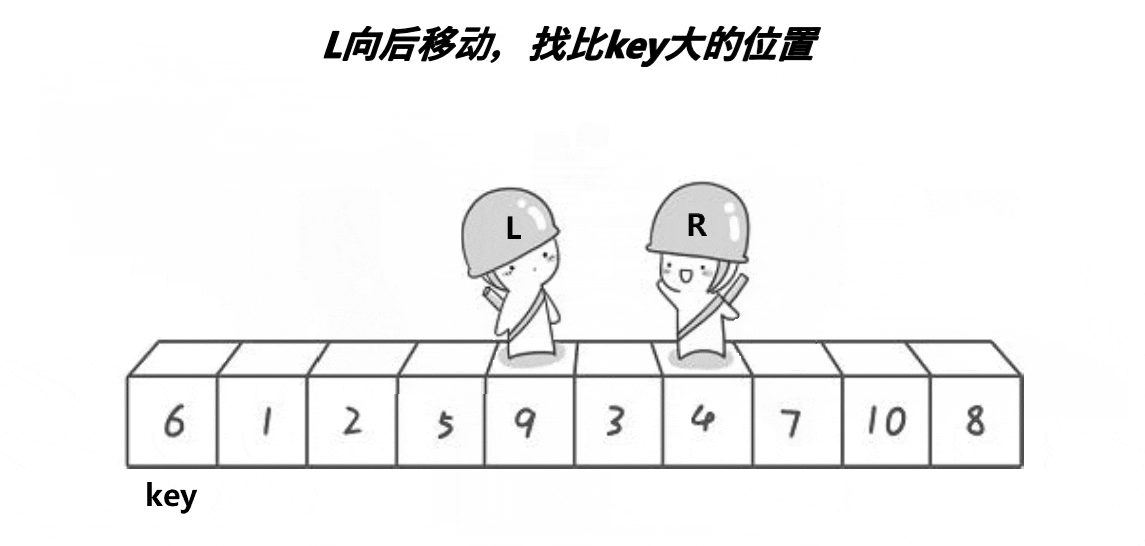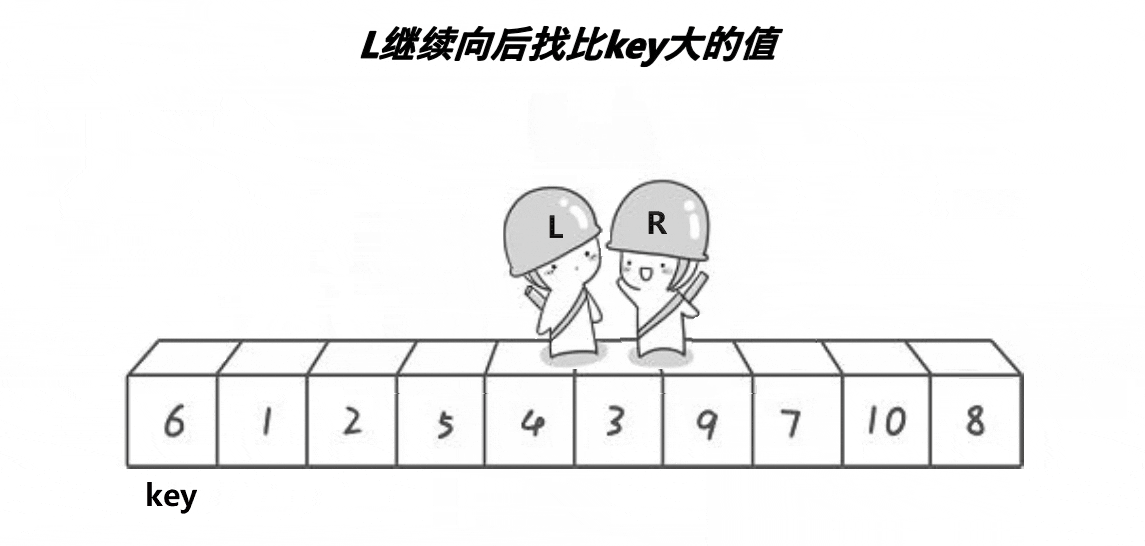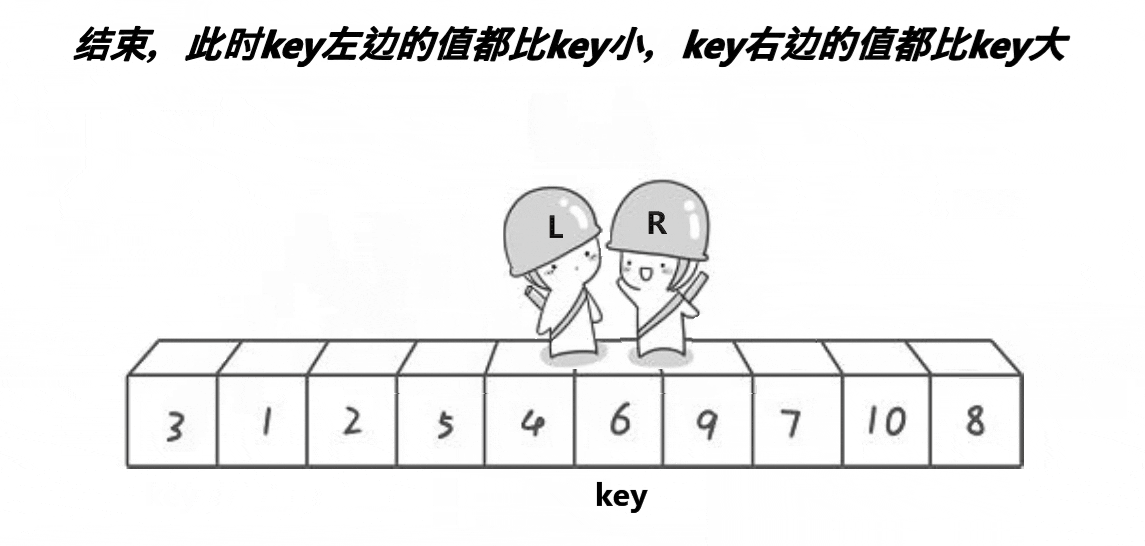
Hoare版本是一种非常巧妙的版本，其思路大致为（以排升序为例）

1. 确定一个key值，然后右找较大值，左找较小值
2. 交换，直到左右相遇，
3. 相遇时， 相遇位置的值一定小于key值（取决于先找大还是先找小，先找大，则为较小值，否则反之），交换key 与 相遇位置的值。
4. 此时满足左边都比key小，右边都比key大
5. 然后再分别进行左部分和右部分的排序。
6. 全部递归完毕，排序完成。
   

代码实现

//交换函数
void Swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
//key 取中位数
int getmidi(int *a,int begin,int end) {int midi = (begin + end) / 2;if (a[midi] > a[begin]) {if (a[midi] < a[end]) return midi;else if (a[begin] > a[end]) return begin;else return end;}else {//a[midi]<a[begin]if (a[begin] < a[end])	return begin;else if (a[midi] > a[end]) return midi;else return end;
}//Hoare版本快速排序
int PartSort1(int* a, int left, int right) {//取key 为首元素int keyi = left;//开始交换，右找大，左找小while (left < right) {//右找大while (left < right && a[right] >= a[keyi]) {right--;}//左找小while (left < right && a[left] <= a[keyi]) {left++;}//交换Swap(&a[left], &a[right]);}//将key与相遇位置值交换，//满足左边都比key小，右边都比key大Swap(&a[keyi], &a[left]);keyi = left;
}
//快速排序主体
void QuickSort(int* a, int begin, int end) {//递归实现if (begin >= end) return;// 定义左边，右边与key相应位置。int left = begin, right = end ;int keyi = begin;//该步骤优化十分重要。int midi = getmidi(a, begin, end);Swap(&a[left], &a[midi]);//排序int key = PartSort1(a, left, right);QuickSort(a, begin, key-1);QuickSort(a, key+1, end);
}

我们来看看运行效果。

2.1.2 hole版本

Hole版本即为挖坑法，是对Hoare版本的优化，避免了许多容易出现的错误。其基本思路为（排升序为例）

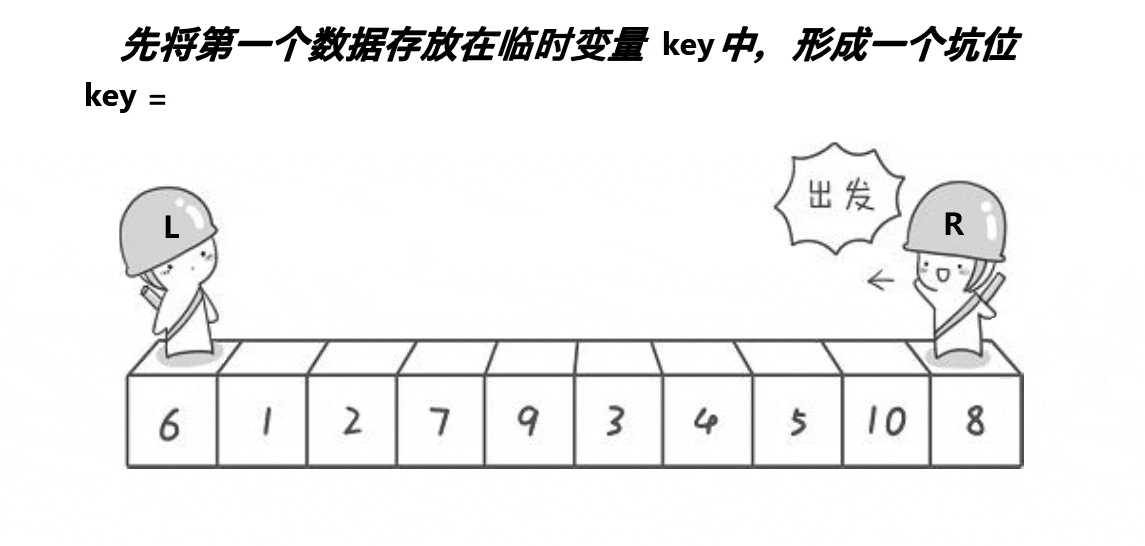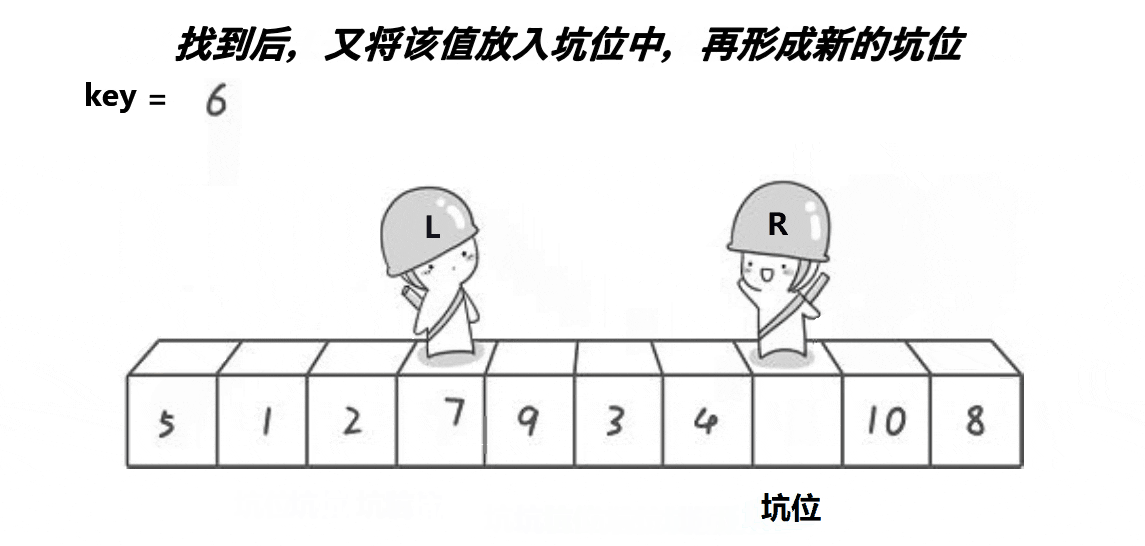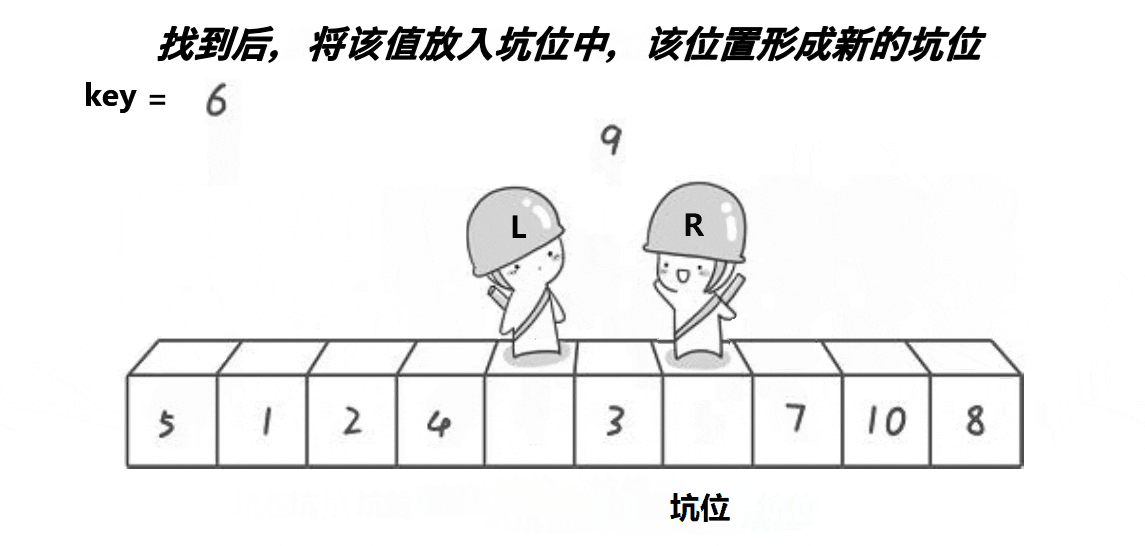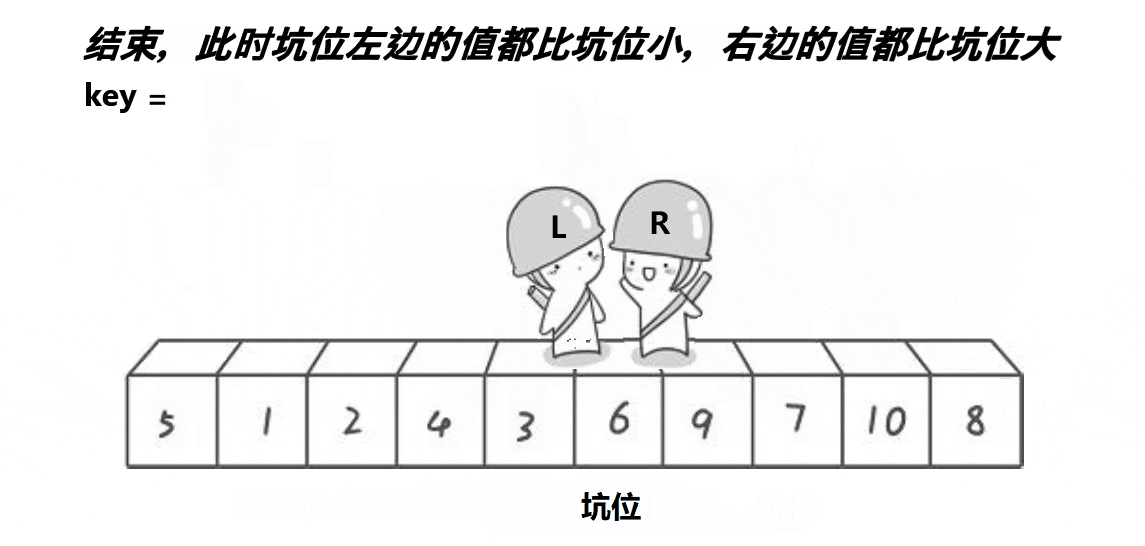
1. 确定一个key值，在该处形成坑位
2. 右找较大值，进入坑位，然后在该较大值处形成新的坑位
3. 左找较小值，进入坑位，然后在该较小值处形成新的坑位。
4. 。。。反复进行至相遇时，把key值放入该坑位。
5. 此时满足左边都比key小，右边都比key大
6. 然后再分别进行左部分和右部分的排序。
7. 全部递归完毕，排序完成。
   

代码实现

主体与上面的Hoare相同，这里提供挖坑法的函数部分。

int PartSort2(int* a, int left, int right) {int key = a[left]; //key取左值int holei = left;//开始排序while(left < right){//右找大while (a[right] >= key && right > left) {right--;}//进坑 挖坑a[holei] = a[right];holei = right;//左找小while (a[left] <= key && right > left) {left++;}//进坑 挖坑		a[holei] = a[left];holei = left;}//结束时，key进坑。完成排序a[holei] = key;return left;
}

2.1.3 前后指针法

前后指针算法是不同于上面两种的独特算法，较为简单。其基本思路为（以排升序为例）：

1. 首先取key值，并定义两个指针，分别指向当前位置与下一位置
2. 如果cur 指向的值比key小，prev++。然后交换prev和cur指针指向的内容
3. cur++;
4. 直到cur到末位置。
5. 交换key和prev指针指向的内容交换。
6. 此时满足左边都比key小，右边都比key大
7. 然后再分别进行左部分和右部分的排序。
8. 全部递归完毕，排序完成。
   

代码实现

主体与上面的Hoare相同，这里提供前后指针法的函数部分。

void Swap(int* p1, int* p2) {int tmp = *p1;*p1 = *p2;*p2 = tmp;
}
int PartSort3(int* a, int begin, int end) {int key = a[begin];int prev = begin, cur = prev + 1;while (cur <= end) {if (a[cur] < key) {prev++;if (prev != cur)Swap(&a[cur], &a[prev]);}cur++;}Swap(&a[begin], &a[prev]);return prev;
}

2.1.4 注意

取中位数

接下来来看两组测试数据，一组为随机十万数据，一组为有序十万数据。
不取中位数版本 与 取中位数版本。

这是肉眼可见的性能提升，防止了再有序情况下的逐个遍历。因此取中位数是很重要的一步，当然一般情况下不会遇到最坏情况。

局部优化

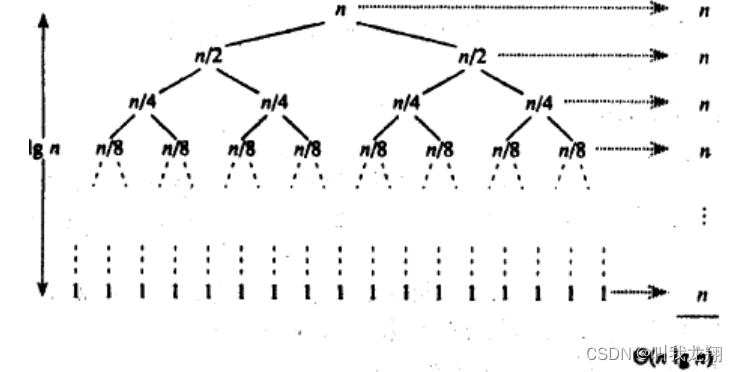
根据二叉树的相关知识，最后一层包含50%数据，倒数第二层包含25%数据，倒数第三层包含12.5%数据。
第n层 递归 1 次 第 n-1 层 递归 2 次 第 n - 2 层 递归 4 次 … 第 1 层 递归 2^n 次
所以在进行绝大部分的排序后，如果继续进行递归会存在问题，此时递归次数非常多。所以我们进行局部优化，在数据小于10个（取决于具体数据）时改换为插入排序等稳定算法即可。

2.1.5 非递归版本

非递归算法通常要使用一些循环来达到全部遍历的目的。也使得 非递归版本 比 递归版本 更需要对“递归”的深入理解，这里快速排序的非递归版本使用栈来模拟递归过程。

非递归原理

先看递归的实现过程，先对整体排，然后排左部分，排右部分。接着对左进行相同处理，对右进行相同处理。
这样的过程可以通过栈来实现（当然使用数组进行指定操作也可以）

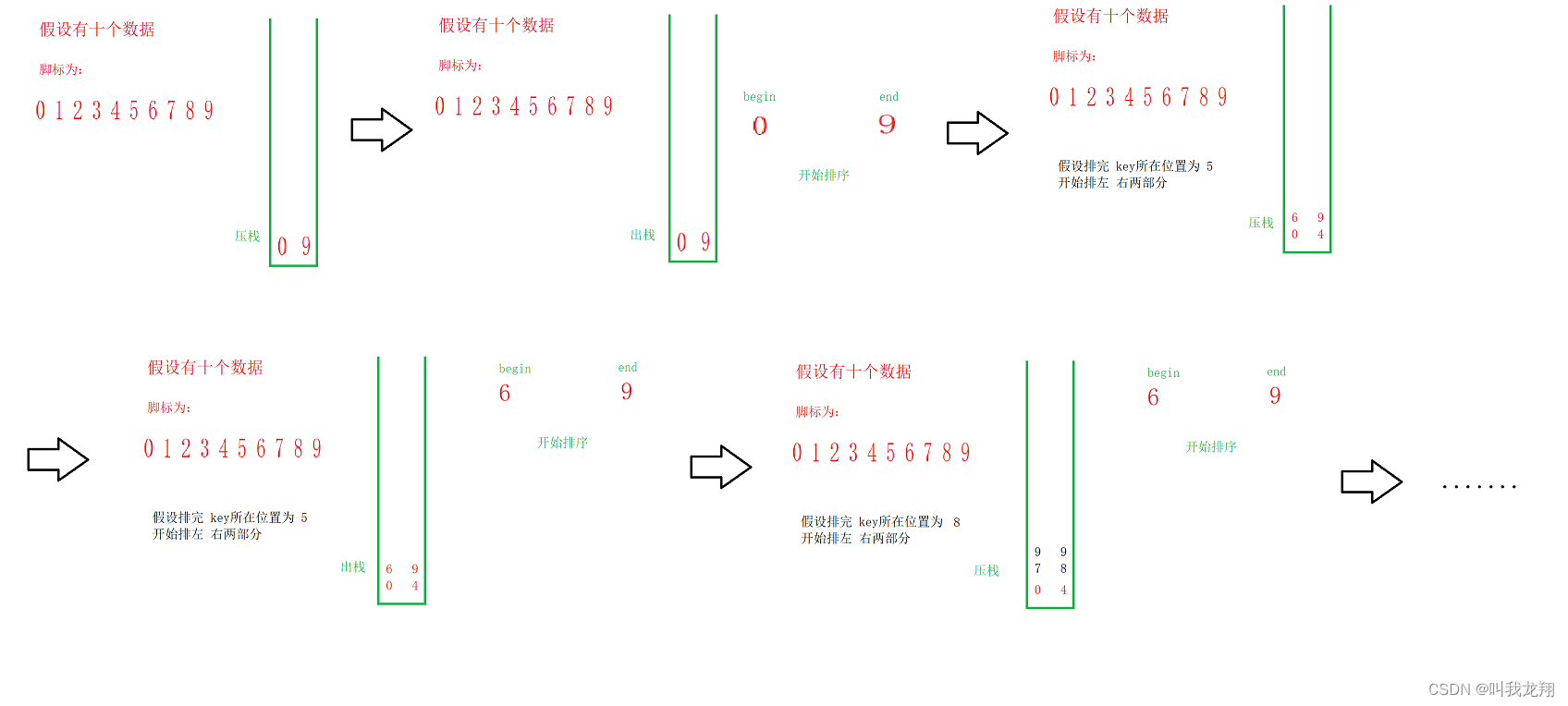
栈里面依次存放了应该排序的部分，每次取出两个，来进行排序（注意取出顺序与存入顺序相反，若先入左 则先取的为右），排序完毕，存入左右部分的开始位置与结束位置，直到有序。
排序步骤

1. 存入开始位置begin 结束位置end ，key值取左值。
2. 依次出栈 记录右位置 right ，左位置 left（读取顺序很重要），排序 该部分
3. 以key值分割左右两部分，压栈存入左部分的开始与结束位置，压栈存入右部分的开始与结束位置。(若left >= key不读取左部分 若 right<=key 不读取右部分)
4. 依次出栈 记录右位置 right ，左位置 left（读取顺序很重要），排序 该部分
5. 重复2 - 3步骤,直到栈为空。
6. 完成排序

代码实现

需要使用栈的相应函数，栈的具体内容请看
栈相关知识

//非递归排序
void QuickSortNonR(int* a, int begin, int end) {//建立栈Stack s ;StackInit(&s);//初始化//压入开始与结束位置StackPush(&s, begin);StackPush(&s, end);//开始排序while (!StackEmpty(&s)) {//不为空就继续进行//出栈读入右位置int right = StackTop(&s);//读取后删除StackPop(&s);//出栈读入左位置int left = StackTop(&s);//读取后删除StackPop(&s);//对该部分进行排序 这里使用前后指针法（使用三种其一即可）int keyi = PartSort3(a, left, right);//读取左部分 若left>=key不进行读入if (left < keyi) {//入栈 StackPush(&s, left);StackPush(&s, keyi - 1);}//读取右部分 若right<=key不进行读入if (right > keyi) {//入栈StackPush(&s, keyi + 1);StackPush(&s, right);}		}
}

2.2 特性总结

快速排序的特性总结：

1. 快速排序整体的综合性能和使用场景都是比较好的，所以才敢叫快速排序

2. 时间复杂度：O(N*logN)
   

3. 空间复杂度：O(logN)

4. 稳定性：不稳定
   总的来说快速排序的内容十分丰富。我个人感觉使用前后指针来实现快速排序比较简单。同时非递归版本可以让我们更深刻的认识递归过程。而且不同版本的性能大差不差，基本相同。

谢谢阅读Thanks♪(･ω･)ﾉ

下一篇文章见！！！