第三部分、栈(Stack)和队列(Queue)详解

栈和队列,严格意义上来说,也属于线性表,因为它们也都用于存储逻辑关系为 "一对一" 的数据,但由于它们比较特殊,因此将其单独作为一章,做重点讲解。
使用栈结构存储数据,讲究“先进后出”,即最先进栈的数据,最后出栈;使用队列存储数据,讲究 "先进先出",即最先进队列的数据,也最先出队列。
既然栈和队列都属于线性表,根据线性表分为顺序表和链表的特点,栈也可分为顺序栈和链表,队列也分为顺序队列和链队列,这些内容都会在本章做详细讲解。
五、[数据结构实践项目]括号匹配算法(C语言实现)
在编写代码的时候,经常会用到两种括号:圆括号 “()” 和大括号 “{}” 。不管使用哪种括号,程序编译没有问题的其中一个重要因素就是所使用的括号是否能够匹配上.
在编写程序时,括号可以嵌套,即: “({()})” 这种形式,但 “({)” 或者 “({}” 都不符合要求。
括号匹配项目要求:给出任意搭配的括号,判断是否匹配。
1、设计思路
编写程序判断括号匹配问题的时候,使用栈结构会很容易:
- 如果碰到的是左圆括号或者左大括号,直接压栈;
- 如果碰到的是右圆括号或者右大括号,就直接和栈顶元素配对:如果匹配,栈顶元素弹栈;反之,括号不匹配;
2、实现代码
#include <stdio.h>
#include <string.h>
int top=-1;//top变量时刻表示栈顶元素所在位置
void push(char * a,int elem){
a[++top]=elem;
}
void pop(char* a){
if (top==-1) {
return ;
}
top--;
}
char visit(char * a){
//调取栈顶元素,不等于弹栈,如果栈为空,为使程序不发生错误,返回空字符
if (top!=-1) {
return a[top];
}else{
return ' ';
}
}
int main() {
char a[30];
char bracket[100];
printf("请输入括号序列:");
scanf("%s",bracket);
getchar();
int length=(int)strlen(bracket);
for (int i=0; i<length; i++) {
//如果是左括号,直接压栈
if (bracket[i]=='('||bracket[i]=='{') {
push(a, bracket[i]);
}else{
//如果是右边括号,判断与栈顶元素是否匹配,如果匹配,栈顶元素弹栈,程序继续运行;否则,发现括号不匹配,输出结果直接退出
if (bracket[i]==')') {
if (visit(a)=='(') {
pop(a);
}else{
printf("括号不匹配");
return 0;
}
}else{
if (visit(a)=='{') {
pop(a);
}else{
printf("括号不匹配");
return 0;
}
}
}
}
//如果所有括号匹配完成,栈内为空,说明所有括号全部匹配成功
if (top!=-1) {
printf("括号不匹配");
}else{
printf("括号匹配");
}
}
运行结果:
请输入括号序列:{}(){
括号不匹配
六、如何用栈结构求表达式的值?
通过前面章节的学习,读者已经了解了什么是栈以及栈存储结构的 2 种实现方式(顺序栈和链栈)。在此基础上,本节教读者用栈解决一个实际问题:如何用栈结构求一个表达式的值?
所谓表达式,就是由变量、常量以及运算符组合而成的式子。其中,常用的运算符无非 !(阶乘运算符)、^(指数运算符)、+、-、*、/ 、( ) 这几种,比如3!+4*2/(1-5)^2就是一个表达式。
那么,如何用栈结构求一个表达式的值呢?实际上,已经有前辈设计好了一种完美的解决方案。
1929 年,波兰逻辑学家 J・卢卡西维兹提出了一种全新的表示表达式的方法,称为后缀表达式或者逆波兰表达式。和普通表达式不同,后缀表达式习惯将运算符写在它的运算项之后,且整个表达式中不用括号 () 表明运算的优先级关系。
以 3! 为例,! 为 运算符,3 为运算项,因此 3! 本身就是一个后缀表达式;再以 4*2 为例,* 为运算符,4 和 2 作为它的运算项,其对应的后缀表达式为 4 2+。
在此基础上,我们试着将 3!+4*2/(1-5)^2 转换成后缀表达式,其过程也就是将表达式中所有运算符放置在它的运算项之后:
- ! 运算符对应的运算项为 3,转换后得到
3 !; - + 运算符对应的运算项是 3! 和 4*2/(1-5)^2,转换之后得到:
3! 4*2/(1-5)^2 +; - * 运算符对应的运算项是 4 和 2,转换之后得到
4 2 *; - / 运算符对应的运算项是 4 2 * 和 (1-5)^2,转换后得到
4 2 * (1-5)^2 /; - - 运算符对应的运算项是 1 和 5,转换后得到
1 5 -; - ^ 运算符对应的运算项是 1 5 - 和 2 ,转换后得到
1 5 - 2 ^。
整合之后,整个普通表达式就转换成了3 ! 4 2 * 1 5 - 2 ^ / +,这就是其对应的后缀表达式。
不难发现,后缀表达式完全舍弃了表达式本该有的可读性,但有失必有得,相比普通表达式,后缀表达式的值可以轻松借助栈存储结构求得。具体求值的过程是:当用户给定一个后缀表达式时,按照从左到右的顺序依次扫描表达式中的各个运算项和运算符,对它们进行如下处理:
- 遇到运算项时,直接入栈;
- 遇到运算符时,将位于栈顶的运算项出栈,对于 ! 运算符,取栈顶 1 个运算项;其它运算符,取栈顶 2 个运算项,第一个取出的运算项作为该运算符的右运算项,另一个作为左运算项。求此表达式的值并将其入栈。
经过以上操作,直到栈中仅存在一个运算项为止,此运算项即为整个表达式的值。
以3 ! 4 2 * 1 5 - 2 ^ / +表达式为例,求值的过程为:
1) 从 3 开始,它是运算项,因此直接入栈:

2) ! 作为运算符,从栈顶取 1 个运算项(也就是 3),求 3! 的值(3! = 3*2*1=6)并将其入栈:

3) 将 4 和 2 先后入栈:

4) 对于 * 运算符,取栈顶 2 个运算项( 2 和 4),其中先取出的 2 作为 * 的右操作数,4 作为左操作数。求的 4* 2 的值 8 ,并将其入栈:

5) 将 1 和 5 先后入栈:

6) 对于 - 运算符,取栈顶 2 个运算项(5 和 1),计算出 1-5 的值为 -4,将其入栈:

7) 将 2 入栈:

8) 对于 ^ 运算符,取栈顶 2 个运算项(2 和 -4),计算出 -4^2 的值 16 ,将其入栈

9) 对于 / 运算符,取栈顶 2 个运算项(16 和 8),计算出 8/16 的值 0.5,将其入栈:

10) 对于 + 运算符,取栈顶 2 个运算符(0.5 和 6),计算出 6+0.5 的值 6.5,将其入栈:

由此,整个求值的过程就结束了,最终表达式的值为 6.5。如下给出了实现此过程的参考代码:
//根据给定的后缀表达式 postexp,计算它的值
typedef struct
{
double data[MAXSIZE];
int top;
}Stack_num;
void InitStack_num(Stack_num **s)
{
*s = (Stack_num *)malloc(sizeof(Stack_num));
(*s)->top = -1;
}
bool Push_num(Stack_num **s, double e)
{
if ((*s)->top == MAXSIZE - 1)
return false;
(*s)->top++;
(*s)->data[(*s)->top] = e;
return true;
}
bool Pop_num(Stack_num **s, double *e)
{
if ((*s)->top == -1)
return false;
*e = (*s)->data[(*s)->top];
(*s)->top--;
return true;
}
//计算后缀表达式的值
double compvalue(char *postexp)
{
Stack_num *num;
int i = 1;
double result;
double a, b;
double c;
double d;
InitStack_num(&num);
//依次扫描整个表达式
while (*postexp != '\0')
{
switch (*postexp)
{
case '+':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算 b+a 的值
c = b + a;
Push_num(&num, c);
break;
case '-':
//计算 b-a 的值
Pop_num(&num, &a);
Pop_num(&num, &b);
c = b - a;
Push_num(&num, c);
break;
case '*':
Pop_num(&num, &a);
Pop_num(&num, &b);
//计算 b*a 的值
c = b * a;
Push_num(&num, c);
break;
case '/':
Pop_num(&num, &a); // a是除数
Pop_num(&num, &b);
//计算 b/a 的值
if (a != 0)
{
c = b / a;
Push_num(&num, c);
}
else
{
printf("除0错误!\n");
exit(0);
}
break;
case '^':
Pop_num(&num, &a); // a是指数
Pop_num(&num, &b);
//计算 b^a 的值
if (a != 0)
{
i = 1;
c = 1;
while(i <= a) {
c = c * b;
i++;
}
}
else if(b != 0)
{
c = 1;
}
else {
c = 0;
}
Push_num(&num, c);
break;
case '!':
Pop_num(&num, &a);
//计算 a! 的值
c = 1;
i = a;
while (i != 0) {
c = c * i;
i--;
}
Push_num(&num, c);
break;
default:
//如果不是运算符,就只能是字符形式的数字,将其转换成对应的整数
d = 0;
while (*postexp >= '0' && *postexp <= '9')
{
d = 10 * d + (*postexp - '0');
postexp++;
}
Push_num(&num, d);
}
postexp++; //继续下一个字符
}
Pop_num(&num, &result);
return result;
}
根据上面的讲解,我们学会了如何求后缀表达式的值。但对于普通用户来讲,另其输入一个正确的后缀表达式显然是不实现的,我们只能要求他们输入一个正确的普通表达式。这就引出了一个问题,即如何将一个普通表达式转换成后缀表达式?
1、后缀表达式的转换
幸运的是,针对这个问题,伟人迪杰斯特拉给出了一个完美的解决方案,称为调用场算法,该算法可以实现将一个普通表达式转换成后缀表达式。
调用场算法的实现,需要借助一个空栈(假设栈名为 Optr)和一个空数组(假设数组名为 postexp)。对于给定的一个普通表达式,调用场算法的转换过程是:逐个遍历表达式中的每个字符:
- 如果为 '0'~'9' 的字符,将其添加到 postexp 数组的末尾;
- 如果该字符为除 ‘(’ 和 ')' 以外的运算符,将其与 Optr 栈顶的运算符进行大小比较,如果该运算符大于栈顶运算符,则将其入栈;反之,如果该运算符小于栈顶运算符,则将栈顶运算符出栈并添加到 postexp 数组的尾部,然后继续拿当前运算符同新的栈顶运算符做大小比较,以此类推。
- 如果该字符为 '(' 运算符,直接入栈;如果为 ')' 运算符,依次取 Optr 栈顶运算符并将其添加到 postexp 数组末尾,直到遇到 '(' 字符为止(注意,'(' 字符也从栈顶取出,但不将其添加 postexp 数组中)。
依照以上处理过程,直到将普通表达式遍历完毕,如果 Optr 栈中仍有运算符,依次将它们出栈并添加到 postexp 数组尾部。最终,postexp 数组内存储的表达式就是转换后的后缀表达式。
值得一提的是,第 2 步中关于运算符的大小比较,迪杰斯塔拉给出了如下所示的表格:
| 当前运算符 | |||||||
|---|---|---|---|---|---|---|---|
| + | - | * | / | ^ | ! | ||
| 栈顶运算符 | + | > | > | < | < | < | < |
| - | > | > | < | < | < | < | |
| * | > | > | > | > | < | < | |
| / | > | > | > | > | < | < | |
| ^ | > | > | > | > | > | < | |
| ! | > | > | > | > | > | > | |
| ( | < | < | < | < | < | < | |
如表 1 所示,假设栈顶运算符为 *,当前遍历到的运算符为 +,则根据表 1 中第 3 行第 1 列可知,* > +(注意不是 + > * ),即当前运算符小于栈顶运算符。根据调用场算法的处理规则,需将 * 出栈并添加到 postexp 数组的尾部,继续用 + 运算符同新的栈顶运算符做比较,以此类推。
以3!+4*2/(1-5)^2为例,接下来为大家演示调用场算法的整个转换过程。遍历整个表达式:
1) 对于字符 3,直接将其添加 postexp 数组的尾部:

2) 遍历至 !,将其与 Optr 栈顶字符进行比较,由于此时 Optr 为空栈,因此直接将 ! 入栈:

3) 遍历至 +,Optr 栈顶运算符! > +,将 ! 从 Optr 栈中取出并添加到 postexp 数组末尾。此时,Optr 栈为空,将 + 入栈:
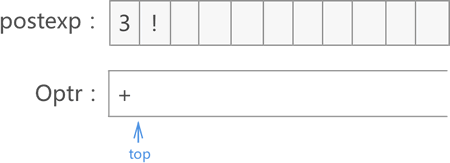
4) 遍历至 4,直接添加到 postexp 数组末尾:

5) 遍历至 *,Optr 栈顶运算符+ < *,所以将 * 入栈:
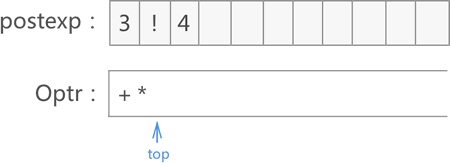
6) 遍历至 2,将其添加至 postexp 数组的末尾:
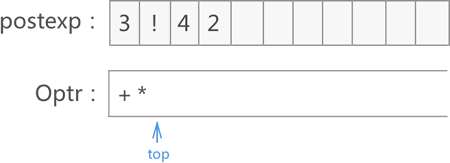
7) 遍历至 /,Optr 栈顶运算符* > /,将 * 取出并添加到 postexp 数组末尾:
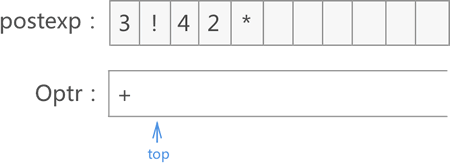
继续用 / 同 Optr 栈顶的 + 运算符比较,+ < /,将 / 入栈:
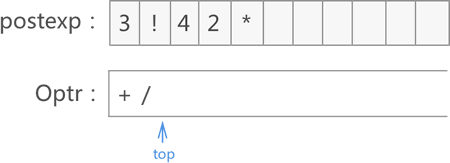
8) 遍历至 (,直接入栈:
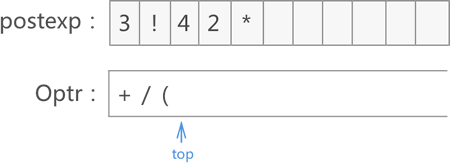
9) 遍历至 1 ,将其添加到 postexp 数组末尾:
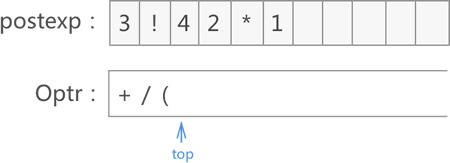
10) 遍历至 -,Optr 栈顶运算符( < -,将 - 入栈:
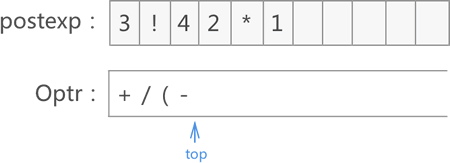
11) 遍历至 5,添加到 postexp 数组末尾:
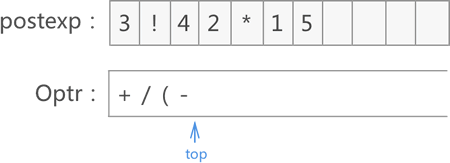
12) 遍历至 ),对 Optr 栈一直做出栈操作并将出栈元素添加到 postexp 数组末尾,直到将 ( 取出:

13) 遍历至 ^,Optr 栈顶运算符/ < ^,将 ^ 入栈:
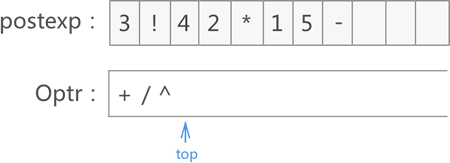
14) 遍历至 2,将其添加到 postexp 数组末尾:
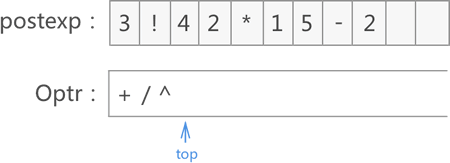
15) 将 Optr 栈做出栈操作,并逐个将出栈元素添加到 postexp 数组末尾,直至 Optr 栈为空:

显然,postexp 数组中存储的就是3!+4*2/(1-5)^2对应的后缀表达式。
如下为调度场算法的实现代码:
// 字符栈
typedef struct
{
char data[MAXSIZE];
int top;
}Stack;
void InitStack(Stack **s)
{
*s = (Stack*)malloc(sizeof(Stack));
(*s)->top = -1;
}
bool Push(Stack *s, char e)
{
if (s->top == MAXSIZE - 1)
return false;
s->top++;
s->data[s->top] = e;
return true;
}
bool Pop(Stack **s, char *e)
{
if ((*s)->top == -1)
return false;
*e = (*s)->data[(*s)->top];
(*s)->top--;
return true;
}
bool GetTop(Stack **s, char *e)
{
if ((*s)->top == -1)
return false;
*e = (*s)->data[(*s)->top];
return true;
}
bool StackEmpty(Stack **s)
{
if ((*s)->top == -1)
return true;
return false;
}
// 将中缀表达式转换成后缀表达式
void trans(char *exp, char postexp[])
{
int i = 0;
char e;
Stack *Optr;
InitStack(&Optr); //初始化操作符栈,为存储后缀表达式做准备
while (*exp != '\0') // 对每个字符进行判断处理
{
switch (*exp)
{
//单独处理括号
//如果是左括号,直接入栈
case '(':
Push(Optr, '(');
exp++;
break;
//如果为右括号,一直出栈操作,直到将 ( 也出栈
case ')':
Pop(&Optr, &e);
while (e != '(')
{
postexp[i++] = e;
Pop(&Optr, &e);
}
exp++;
break;
// + - 优先级相同,当做同一种情况处理
case '+':
case '-':
//由于 + - 的优先级只比 ( 大,所有只要栈顶字符不为 ( 就一直出栈;反之,则将 + - 入栈。
while (!StackEmpty(&Optr))
{
GetTop(&Optr, &e);
if (e == '(')
break;
else
{
postexp[i++] = e;
Pop(&Optr, &e);
}
}
//最后将 + - 入栈
Push(Optr, *exp);
exp++;
break;
case '*':
case '/':
// * / 优先级比 * / ^ ! 小,所有如果栈顶运算符是它们,就出栈;反之就将 * / 入栈
while (!StackEmpty(&Optr))
{
GetTop(&Optr, &e);
if (e == '/' || e == '*' ||e=='^' || e=='!') // * / 的优先级仅仅低于它前面的 * /,高于前面的 + -,所以要将前面的 * / 弹出栈;+ - 保留,因为新的 * / 会放在栈低,优先级高。
{
postexp[i++] = e;
Pop(&Optr, &e);
}
else
break; // 其他情况( + - 左括号 )退出,
}
//最后将 / * 入栈
Push(Optr, *exp);
exp++;
break;
case '^':
// ^ 优先级仅比 ^ ! 小,如果栈顶运算符是它们,则出栈;反之将 ^ 入栈
while (!StackEmpty(&Optr))
{
GetTop(&Optr, &e);
if (e == '^' || e == '!')
{
postexp[i++] = e;
Pop(&Optr, &e);
}
else
break; // 其他情况( + - * / ( )退出,
}
Push(Optr, *exp); //最后将 ^ 入栈
exp++;
break;
case '!':
// ! 优先级仅比 ! 小,所有如果栈顶运算符为 !,则将其出栈;反之,将 ! 入栈
while (!StackEmpty(&Optr))
{
GetTop(&Optr, &e);
if (e == '!')
{
postexp[i++] = e;
Pop(&Optr, &e);
}
else
break; // 其他情况( + - * / ^ ( )退出,
}
//最后将 ! 入栈
Push(Optr, *exp);
exp++;
break;
default:
while (*exp > '0' && *exp < '9') //循环判断是否为数字字符,如果是则保存到postexp,循环判断是因为可能是多位数字
{
postexp[i++] = *exp;
exp++;
}
//以#分隔各个数字字符
postexp[i++] = '#';
}
}
while (!StackEmpty(&Optr)) //扫描完exp后,操作符栈可能还有操作符,将其存到postexp
{
Pop(&Optr, &e);
postexp[i++] = e;
}
postexp[i] = '\0'; //结束字符串
free(Optr); //销毁栈
}
由此,用栈结构求表达式的值的完整解决方案为:
- 将用户输入的普通表达式,借助调用场算法转换为后缀表达式;
- 由第一步得到的后缀表达式,计算出它的值。
为了方便读者理解整个用栈求表达式的值的过程,本文给大家提供了可直接编译运行的源码(点击栈求表达式的值即可下载)。