上次讲了选择排序和堆排序：数据结构排序——选择排序与堆排序

今天就来快排和冒泡

---

---

1.快排

1.1基本介绍

快速排序（Quick Sort）是一种常用的排序算法，它是由英国计算机科学家Tony Hoare于1959年发明的。快速排序的基本思想是通过分治的策略将一个数组分成两个子数组，然后分别对这两个子数组进行排序。具体步骤如下：

1. 选择一个基准元素（通常是数组的第一个元素，右边先行）。
2. 将数组分割成两部分，使得左边的元素都小于等于基准元素，右边的元素都大于基准元素。这个过程叫做分区（Partition）
3. 对分割后的两个子数组分别重复步骤1和2（利用递归），直到子数组的大小为1或0，此时数组已经有序

==优化：==如果本身就很接近有序，那效率就慢了（一个逆序变升序，keyi就一直在左边，递归也只有右侧，所以选择三个数来找中间大小，能让keyi尽量向数组中间靠近），所以设计了Getmid函数来取中间大小的数

1.2不同的分区方法及代码实现

1.2.1Hoare版

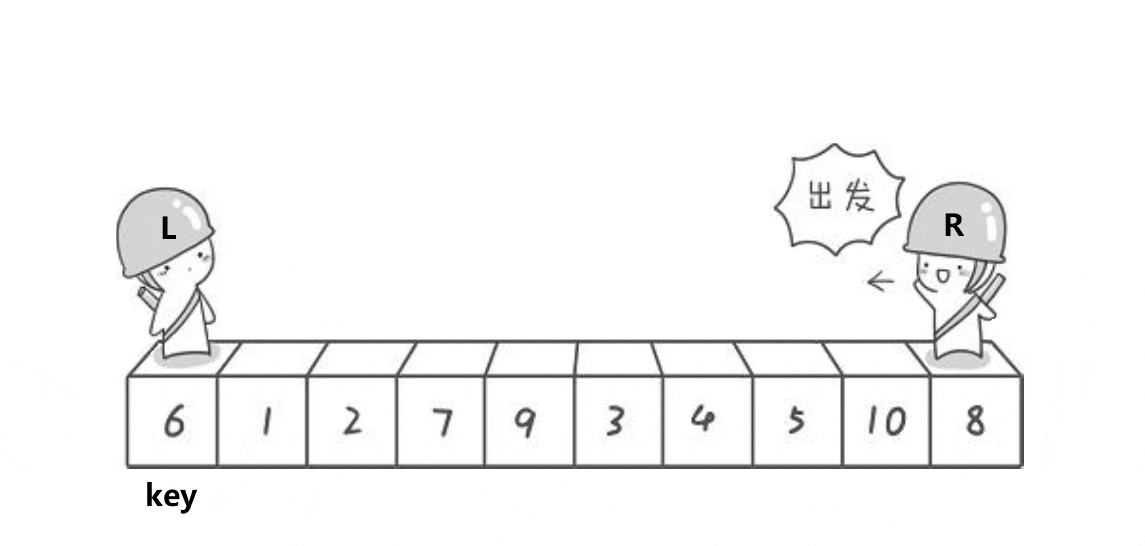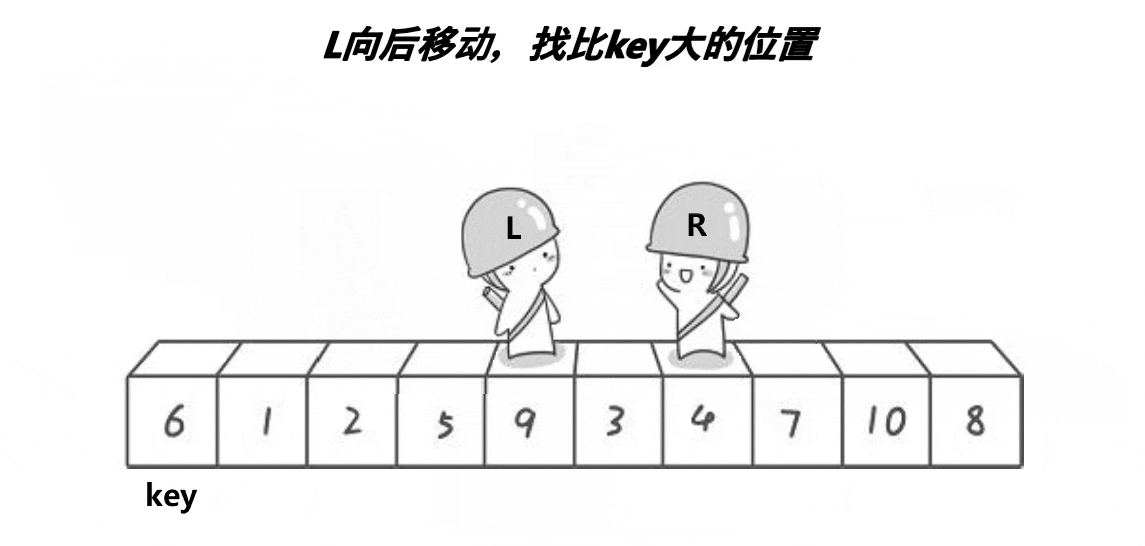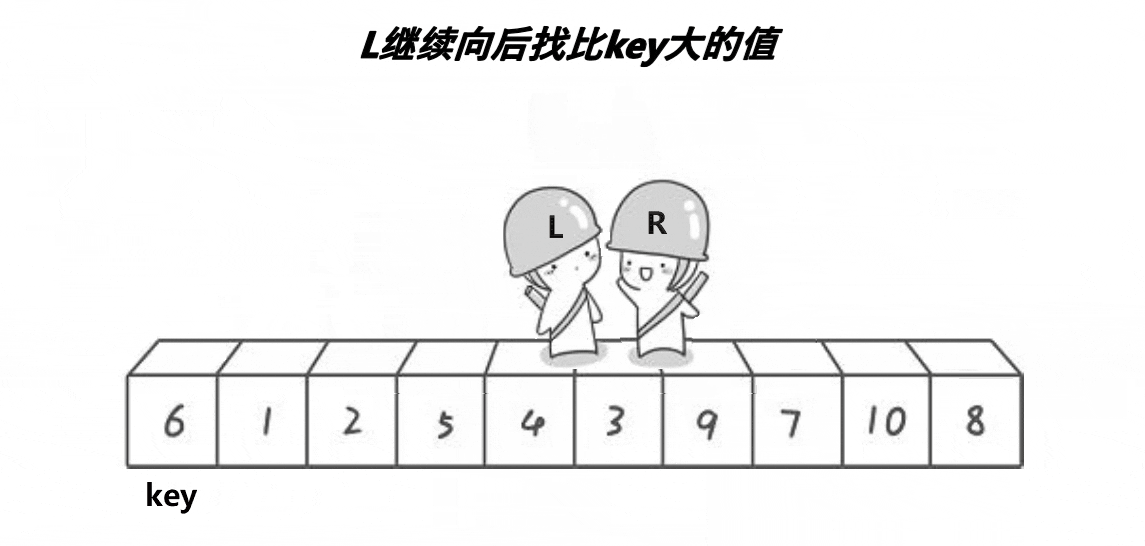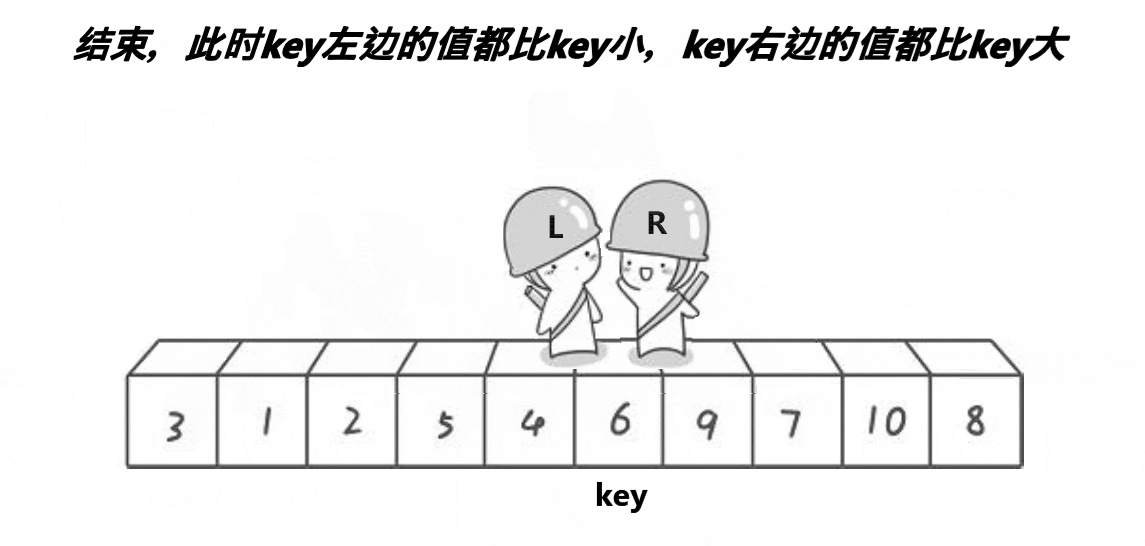
使用两个索引，一个从数组的左边开始向右移动，另一个从数组的右边开始向左移动，直到它们相遇。在这个过程中，如果左指针指向的元素大于基准元素且右指针指向的元素小于基准元素，则交换这两个元素。当两个指针相遇时，将基准元素（keyi指向的）与相遇位置的元素交换，这样基准元素就归位了

void Swap(int* x, int* y)
{int tmp = *x;*x = *y;*y = tmp;
}int GetMid(int* a,int left, int right)//找中间的
{// a[left]      a[mid]           a[right]int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right])  // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[left] < a[right]){return left;}else if (a[mid] < a[right]){return right;}else{return mid;}}
}
//一次排序
int OneSort1(int* a, int left, int right)//使keyi位置的元素处于正确的位置上
{int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);//现在left处是三者的中间值了//左边第一个为key，右边先走才能保证相遇处比啊a[keyi]小int keyi = left;while (left < right){while (a[right] >= a[keyi] && left < right)//右边先走{right--;}while (a[left] <= a[keyi] && left < right)//左侧找大的{left++;}Swap(&a[left], &a[right]);//找到一个大和一个小的就交换}Swap(&a[keyi], &a[left]);//把keyi放相遇位置return left;//返回相遇的索引
}void QuickSort(int* a, int begin, int end)//升序
{if (begin >= end){return;}// [begin, keyi-1] keyi [keyi+1, end]int keyi = OneSort1(a, begin, end);//找到keyi索引，才能分左右QuickSort(a, begin, keyi - 1);//左侧QuickSort(a, keyi + 1, end);//右侧
}int main()
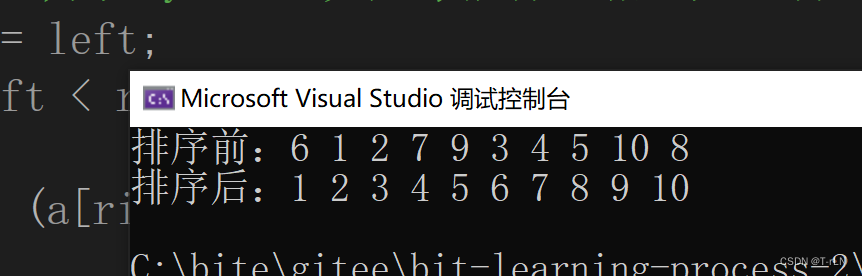
{int a[] = { 6,1,2,7,9,3,4,5,10,8 };printf("排序前：");for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}printf("\n");QuickSort(a, 0,sizeof(a) / sizeof(int)-1);printf("排序后：");for (int i = 0; i < sizeof(a) / sizeof(int); i++){printf("%d ", a[i]);}printf("\n");return 0;
}

1.2.2挖坑版

选择基准元素后，先将基准元素保存到临时变量中，然后使用左右索引的方式找到需要交换的元素，将这些元素填入基准元素的位置，最后将基准元素填入最后一个空出来的位置

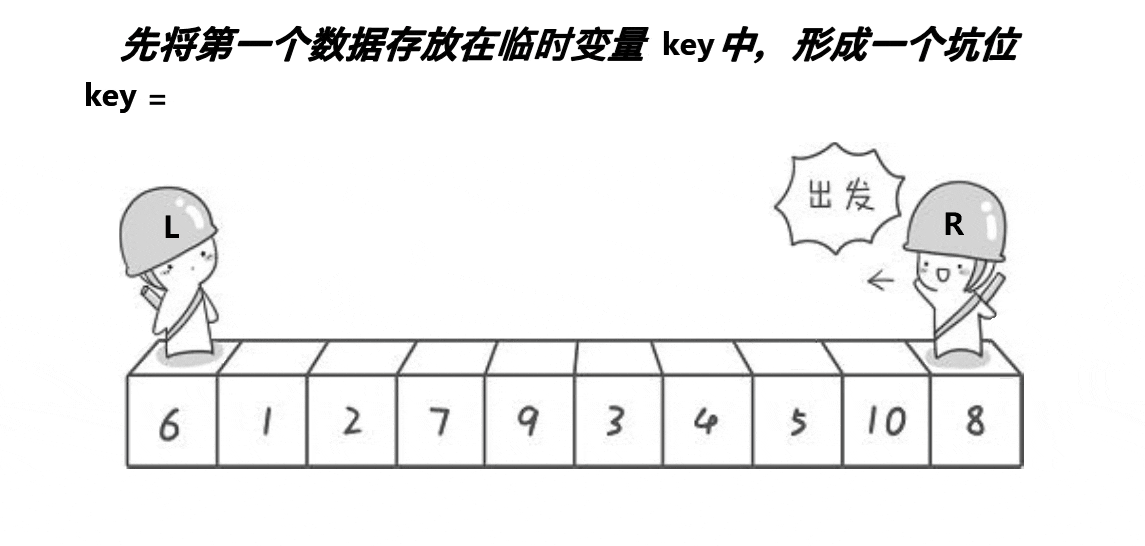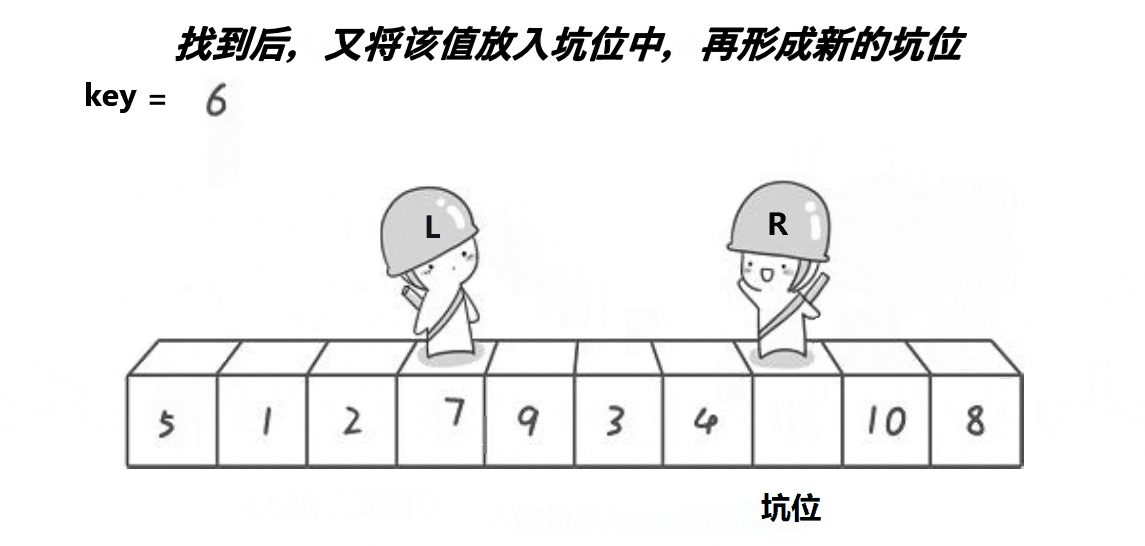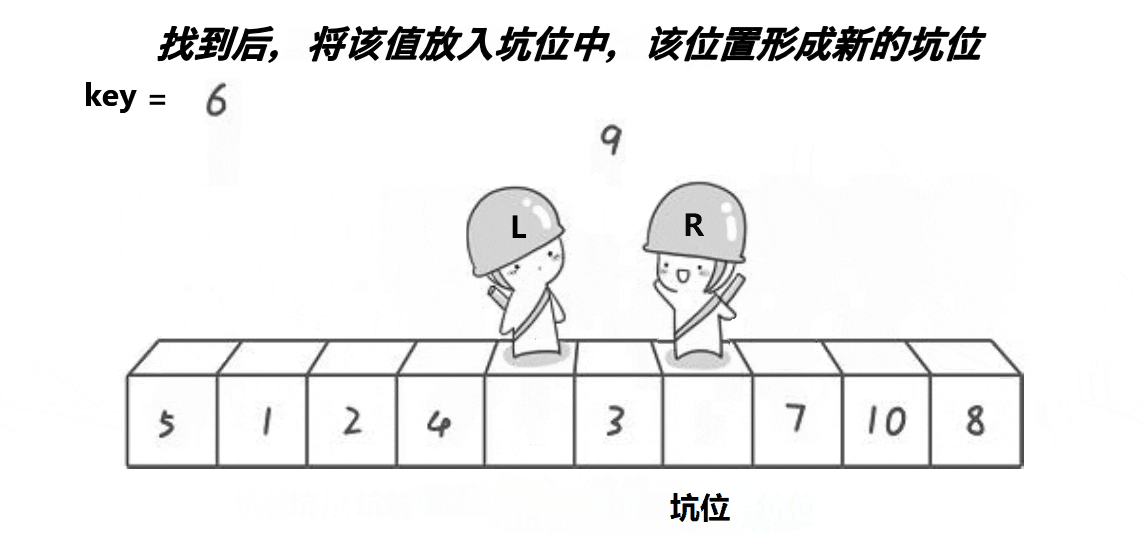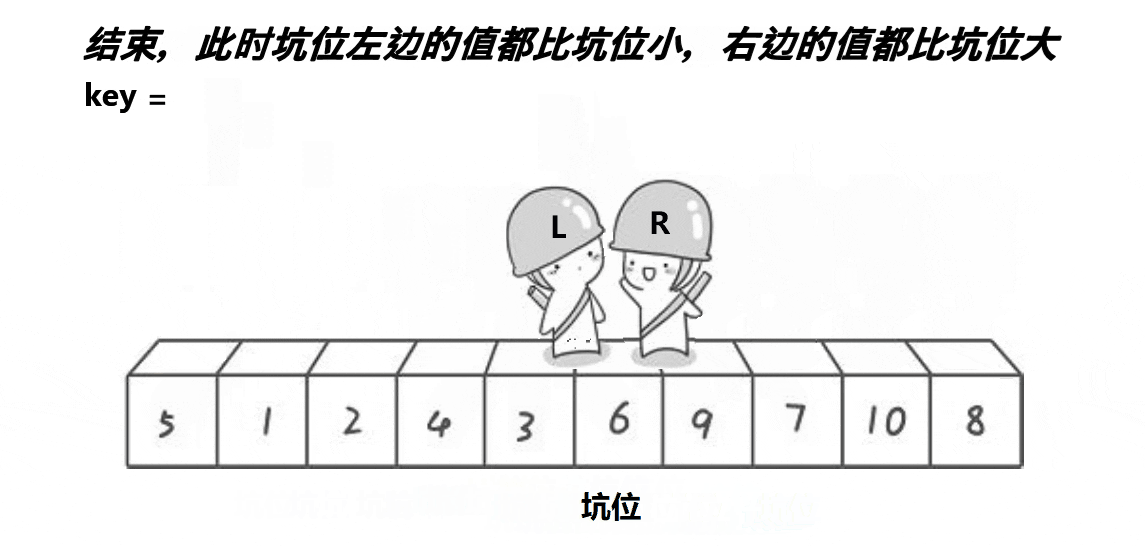
int OneSort2(int* a, int left, int right)//挖坑
{int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);//现在left处是三者的中间值了int key = a[left];//保存基准元素int hole = left;//储存坑下标，不能直接赋值为0while (left < right){while (a[right] >= key && left < right)//右边先走,没有等号两侧出现相同值会死循环{right--;}//找到了就去赋值到第一个“坑”a[hole] = a[right];hole = right;//更新坑while (a[left] <= key && left < right)//左侧找大的{left++;}a[hole] = a[left];hole = left;}Swap(&key, &a[left]);//把keyi放相遇位置return left;//返回相遇的索引
}

1.2.3 前后指针版

pre指向第一个，cur指向下一个。cur找小后，pre++，然后交换（做到大的向后推），最后cur出数组结束

prev的情况有两种：

1. 在cur还没遇到比key大的值时候，prev紧跟着cur
2. 在cur还遇到比key大的值时候，prev在比key大的一组值的前面

本质是把一段大于key的区间，往后推，同时小的甩到左边去

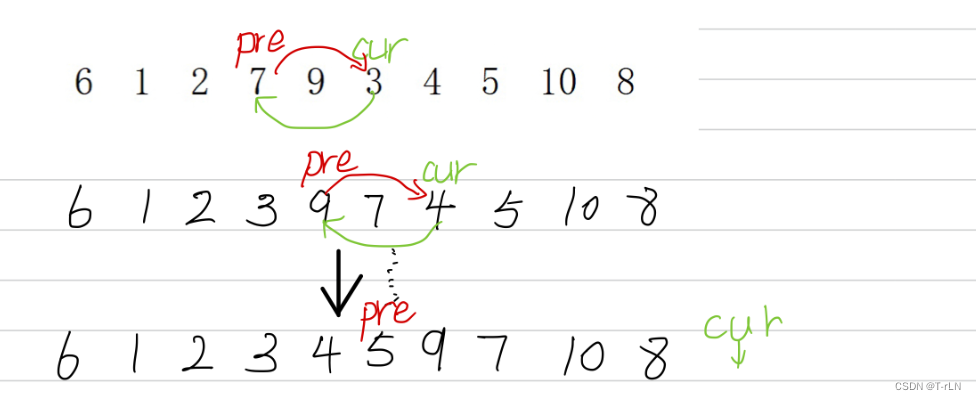
int OneSort3(int* a, int left, int right)//挖坑
{int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);int keyi = left;int pre = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi]){pre++;Swap(&a[cur], &a[pre]);}cur++;}Swap(&a[pre], &a[keyi]);return pre;
}

1.3快排的优化

1.3.1三数取中选key

从待排序数组的首、尾和中间位置各选取一个元素，然后取它们的中间值作为基准元素，确保选择的基准元素相对中间位置的元素更为接近

代码在Hoare版已经展示过了

int GetMid(int* a,int left, int right)//找中间的
{// a[left]      a[mid]           a[right]int mid = (left + right) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right])  // mid是最大值{return left;}else{return right;}}else // a[left] > a[mid]{if (a[left] < a[right]){return left;}else if (a[mid] < a[right]){return right;}else{return mid;}}
}

1.3.2递归到小的子区间时，可以考虑使用插入排序

当递归到小的子区间时，可以考虑使用插入排序来优化快速排序。因为插入排序在小规模数据上的排序效率通常比快速排序更高==(当数量比较少时，也没必要在递归好几层了)==

void InsertSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){int end = i;int tmp = a[end + 1];while (end >= 0){if (a[end] > tmp){a[end + 1] = a[end];}else{break;}end--;}a[end + 1] = tmp;}
}int OneSort3(int* a, int left, int right)//挖坑
{int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);int keyi = left;int pre = left;int cur = left + 1;while (cur <= right){if (a[cur] < a[keyi]){pre++;Swap(&a[cur], &a[pre]);}cur++;}Swap(&a[pre], &a[keyi]);return pre;
}void QuickSort(int* a, int begin, int end)//升序
{if (begin >= end){return;}if ((end - begin + 1) > 10){// [begin, keyi-1] keyi [keyi+1, end]int keyi = OneSort3(a, begin, end);QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}else{//用插入排序InsertSort(a + begin, end - begin + 1);}
}

1.3.3大量重复数据采用三路划分

快速排序的三路划分通过将数组分为小于、等于=和大于基准元素的三个部分==，有效地处理了重复元素，提高了算法的效率

快速排序的三路划分算法的基本思想是使用三个指针/下标来维护三个区域：小于基准元素的区域、等于基准元素的区域和大于基准元素的区域。在每一次遍历数组的过程中，将数组分为这三个区域，并将指针移动到合适的位置。最终，数组会被划分成小于基准元素、等于基准元素和大于基准元素的三个部分

基本步骤：

void QuickSort(int* a, int left, int right)
{if (left >= right){return;}int begin = left;int end = right;int mid = GetMid(a, left, right);Swap(&a[mid], &a[left]);int cur = left + 1;int key = a[left];//储存一下，后面比较来用，用a[left]会被替代while (cur <= right){if (a[cur] < key){Swap(&a[cur], &a[left]);cur++;left++;}else if (a[cur] == key){cur++;}else{Swap(&a[cur], &a[right]);right--;}}QuickSort(a, begin, left - 1);QuickSort(a, right + 1, end);
}

1.4快排非递归

快速排序的非递归实现通常使用栈来模拟递归调用的过程。在快速排序的递归实现中，每次递归调用都将函数参数压入栈中，然后在递归返回时再从栈中弹出参数(二者性质相同)。

非递归实现则需要手动维护一个栈，将需要处理的子序列的起始和结束位置压入栈中，然后循环处理栈中的元素，直到栈为空（递归一次就用一次）

void QuickSortNonR(int* a, int begin, int end)//利用栈，先想好先排左侧再排右侧
{ST st;STInit(&st);STPush(&st,end);//把各个区间的两侧的索引（整形）插入进Stack中STPush(&st,begin);//栈（后进先出），先排左侧所以后入左while (!STEmpty(&st)){int left = STTop(&st);STPop(&st);int right = STTop(&st);STPop(&st);int keyi = OneSort1(a, left, right);//得到基准元素下标// [begin, keyi-1] keyi [keyi+1, end]if (keyi + 1 < right)//等于说明就一个，没必要{STPush(&st, right);STPush(&st, keyi);}if (left < keyi-1){STPush(&st, keyi-1);STPush(&st, left);}}STDestroy(&st);
}

---

2.冒泡排序

它重复地遍历要排序的列表，比较每对相邻的元素，并按照大小顺序交换它们。重复这个过程直到整个列表排序完成

步骤：

1. 从列表的第一个元素开始，依次比较相邻的两个元素，如果它们的顺序不正确就交换它们。
2. 继续遍历列表，重复上述比较和交换的过程，直到没有任何一对相邻元素需要交换为止。
3. 列表排序完

void BobbleSort(int* a, int n)
{for (int i = 0; i < n - 1; i++){for (int j = 0; j < n - 1 - i; j++){if (a[j] > a[j + 1]){Swap(&a[j], &a[j + 1]);}}}
}

---

好啦，这次内容就到这里啦，下次带来归并排序，感谢大家支持！！！