文章目录
- 0 前言
- 1 课题背景
- 2 实现效果
- 3 设计原理
- QTCharts
- arma模型预测
- K-means聚类算法
- 算法实现关键问题说明
- 4 部分核心代码
- 5 最后
0 前言
🔥 优质竞赛项目系列,今天要分享的是
🚩 基于大数据的股票量化分析与股价预测系统
该项目较为新颖,适合作为竞赛课题方向,学长非常推荐!
🥇学长这里给一个题目综合评分(每项满分5分)
- 难度系数:3分
- 工作量:3分
- 创新点:4分
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate
1 课题背景
基于大数据的股票可视化分析平台设计,对股票数据进行预处理,清洗以及可视化分析,同时设计了软件界面。
2 实现效果
价格可视化
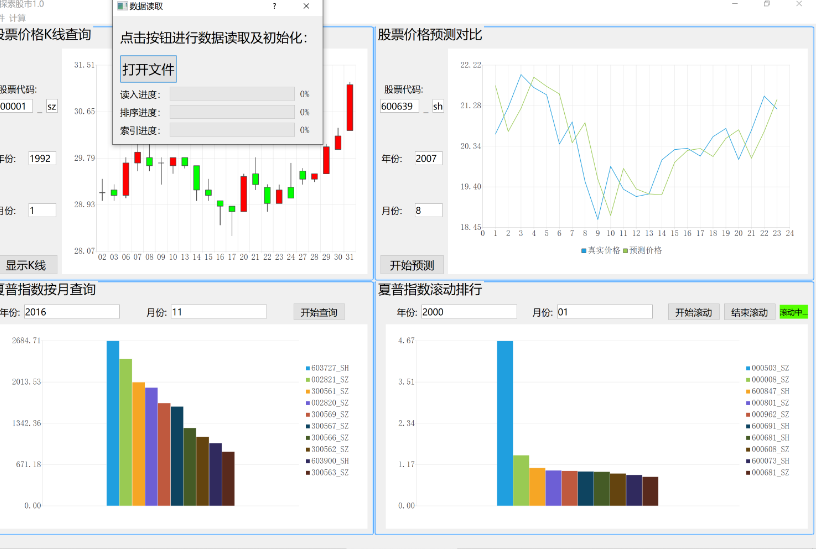
魔梯访问与指标计算
聚类分析

3 设计原理
QTCharts
简介
QtCharts是Qt自带的组件库,其中包含折线、曲线、饼图、棒图、散点图、雷达图等各种常用的图表。而在地面站开发过程中,使用折线图可以对无人机的一些状态数据进行监测,更是可以使用散点图来模拟飞机所在位置,实现平面地图的感觉。
使用Qt
Charts绘制,大概可以分为四个部分:数据(QXYSeries)、图表(QChart)、坐标轴(QAbstractAXis)和视图(QChartView)。这里就不一一给大家介绍了,下面给大家说一下QtCharts的配置安装。
QtCharts模块的C++类
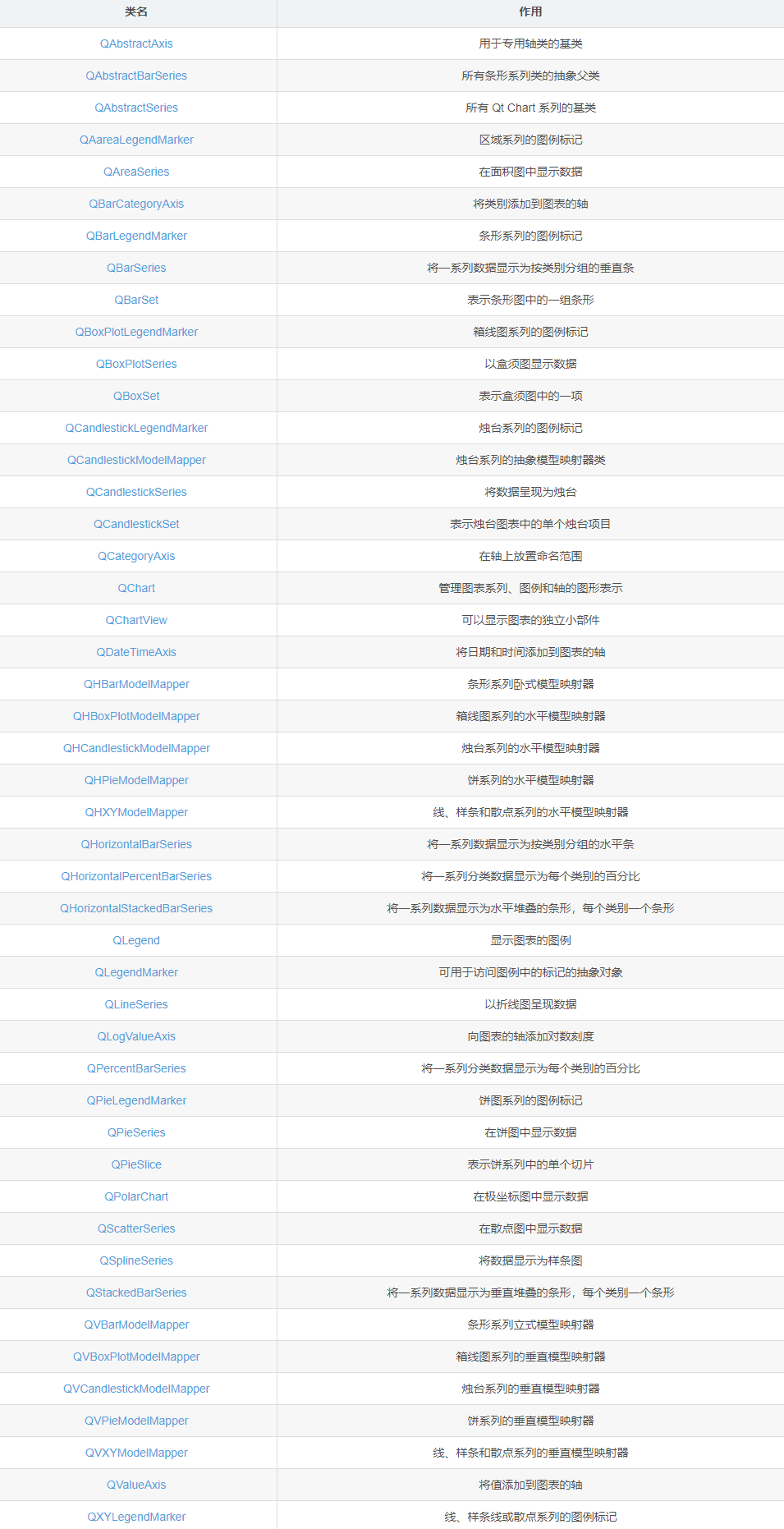
arma模型预测
简介
ARMA模型,又称为ARMA
(p,q)模型。其核心思想就是当前正如名字所显示的,整个模型的核心就是要确定p和q这两个参数。其中,p决定了我们要用几个滞后时期的价格数据,而q决定了我们要用几个滞后时期的预测误差。
简单来说,ARMA模型做了两件事。一是基于趋势理论,用历史数据来回归出一个当前的价格预测,这个预测反映了自回归的思想。但是这个预测必然是有差异的,所以ARMA模型根据历史的预测误差也回归出一个当前的误差预测,这个预测反映了加权平均的思想。用价格预测加上误差预测修正,才最终得到一个理论上更加精确的最终价格预测。
比起简单的自回归模型或者以时间为基础的简单趋势预测模型,ARMA模型最大的优势,在于综合了趋势理论和均值回归理论,理论上的精确度会比较高。
'''自回归滑动平均模型'''from statsmodels.tsa.arima_model import ARMAfrom itertools import product ```
def myARMA(data):p = range(0, 9)q = range(0, 9)parameters = list(product(p, q)) # 生成(p,q)从(0,0)到(9,9)的枚举best_aic = float('inf')result = Nonefor param in parameters:try:model = ARMA(endog=data, order=(param[0], param[1])).fit()except ValueError:print("参数错误:", param)continueaic = model.aicif aic < best_aic: # 选取最优的aicbest_aic = model.aicresult = (model, param)return result
```K-means聚类算法
基本原理
k-Means算法是一种使用最普遍的聚类算法,它是一种无监督学习算法,目的是将相似的对象归到同一个簇中。簇内的对象越相似,聚类的效果就越好。该算法不适合处理离散型属性,但对于连续型属性具有较好的聚类效果。
聚类效果判定标准
使各个样本点与所在簇的质心的误差平方和达到最小,这是评价k-means算法最后聚类效果的评价标准。
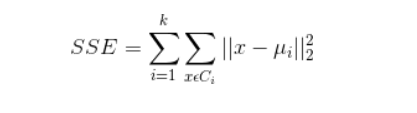
算法实现步骤
1)选定k值
2)创建k个点作为k个簇的起始质心。
3)分别计算剩下的元素到k个簇的质心的距离,将这些元素分别划归到距离最小的簇。
4)根据聚类结果,重新计算k个簇各自的新的质心,即取簇中全部元素各自维度下的算术平均值。
5)将全部元素按照新的质心重新聚类。
6)重复第5步,直到聚类结果不再变化。
7)最后,输出聚类结果。
算法缺点
虽然K-Means算法原理简单,但是有自身的缺陷:
1)聚类的簇数k值需在聚类前给出,但在很多时候中k值的选定是十分难以估计的,很多情况我们聚类前并不清楚给出的数据集应当分成多少类才最恰当。
2)k-means需要人为地确定初始质心,不一样的初始质心可能会得出差别很大的聚类结果,无法保证k-means算法收敛于全局最优解。
3)对离群点敏感。
4)结果不稳定(受输入顺序影响)。
5)时间复杂度高O(nkt),其中n是对象总数,k是簇数,t是迭代次数。
算法实现关键问题说明
K值的选定说明
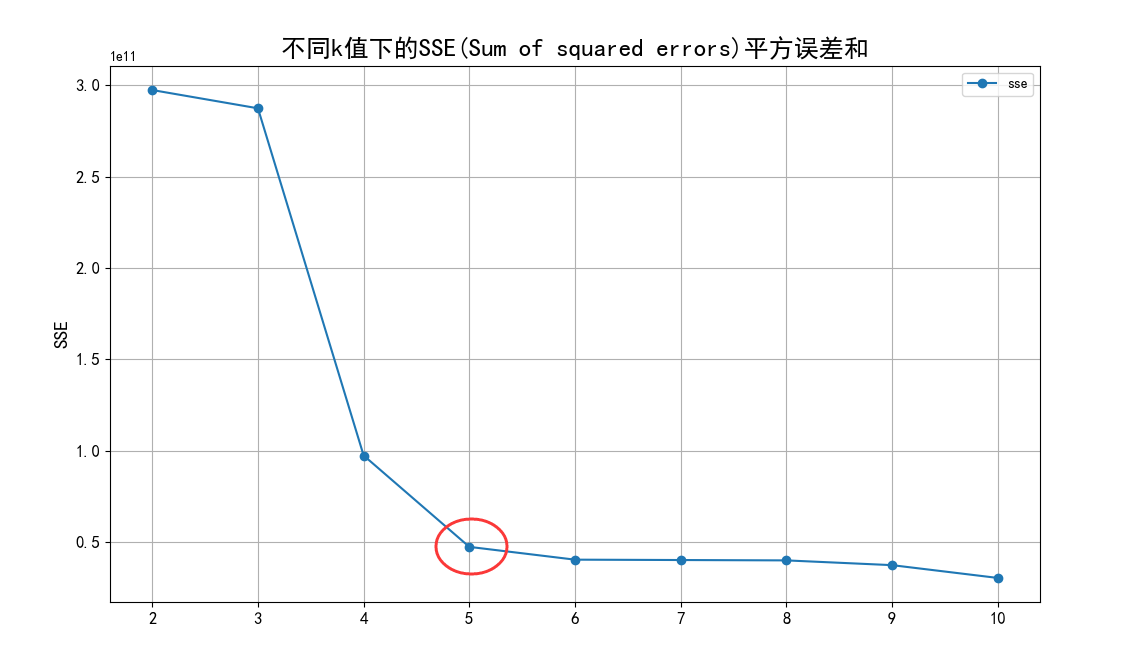
根据聚类原则:组内差距要小,组间差距要大。我们先算出不同k值下各个SSE(Sum of
squared
errors)值,然后绘制出折线图来比较,从中选定最优解。从图中,我们可以看出k值到达5以后,SSE变化趋于平缓,所以我们选定5作为k值。
初始的K个质心选定说明
初始的k个质心选定是采用的随机法。从各列数值最大值和最小值中间按正太分布随机选取k个质心。
关于离群点
离群点就是远离整体的,非常异常、非常特殊的数据点。因为k-
means算法对离群点十分敏感,所以在聚类之前应该将这些“极大”、“极小”之类的离群数据都去掉,否则会对于聚类的结果有影响。离群点的判定标准是根据前面数据可视化分析过程的散点图和箱线图进行判定。
4 部分核心代码
#include "kmeans.h"
#include "ui_kmeans.h"kmeans::kmeans(QWidget *parent) :QDialog(parent),ui(new Ui::kmeans)
{this->setWindowFlags(Qt::Dialog | Qt::WindowMinMaxButtonsHint | Qt::WindowCloseButtonHint);ui->setupUi(this);
}kmeans::~kmeans()
{delete ui;
}void kmeans::closeEvent(QCloseEvent *)
{end_flag=true;
}void kmeans::on_pushButton_clicked()
{end_flag=false;//读取数据QFile sharpe("sharpe.txt");sharpe.open(QIODevice::ReadOnly|QIODevice::Text);std::vector<std::array<double,2>> data;while(!sharpe.atEnd()){QStringList linels=QString(sharpe.readLine()).split(',');qreal mean=linels[3].toDouble();qreal sd=linels[4].toDouble();if(mean>-0.06&&mean<0.06&&sd<0.12)data.push_back({mean,sd});}std::random_shuffle(data.begin(),data.end());sharpe.close();//聚类ui->pushButton->setText("聚类中...");QApplication::processEvents();auto labels=std::get<1>(dkm::kmeans_lloyd(data,9));ui->pushButton->setText("开始");QApplication::processEvents();//作图QChart *chart = new QChart();//chart->setAnimationOptions(QChart::SeriesAnimations);//chart->legend()->setVisible(false);QList<QScatterSeries*> serieses;QList<QColor> colors{QColor(Qt::black),QColor(Qt::cyan),QColor(Qt::red),QColor(Qt::green),QColor(Qt::magenta),QColor(Qt::yellow),QColor(Qt::gray),QColor(Qt::blue),QColor("#A27E36")};for(int i=0;i<9;i++){QScatterSeries *temp = new QScatterSeries();temp->setName(QString::number(i));temp->setColor(colors[i]);temp->setMarkerSize(10.0);serieses.append(temp);chart->addSeries(temp);}chart->createDefaultAxes();/*v4
-------------------------------------------------------------Percentiles Smallest1% -.023384 -.359855% -.0115851 -.349373
10% -.0078976 -.325249 Obs 613,849
25% -.0037067 -.324942 Sum of Wgt. 613,84950% .0000567 Mean .0004866Largest Std. Dev. .0130231
75% .0041332 1.28376
90% .0091571 1.52169 Variance .0001696
95% .0132541 2.73128 Skewness 95.21884
99% .0273964 4.56203 Kurtosis 28540.15v5
-------------------------------------------------------------Percentiles Smallest1% .0073016 4.68e-075% .0112397 7.22e-07
10% .0135353 7.84e-07 Obs 613,849
25% .0180452 8.21e-07 Sum of Wgt. 613,84950% .0248626 Mean .0282546Largest Std. Dev. .0213631
75% .0343356 3.2273
90% .0458472 3.32199 Variance .0004564
95% .0549695 4.61189 Skewness 68.11651
99% .0837288 4.75981 Kurtosis 11569.69*/QValueAxis *axisX = qobject_cast<QValueAxis *>(chart->axes(Qt::Horizontal).at(0));axisX->setRange(-0.06,0.06);axisX->setTitleText("平均值");axisX->setLabelFormat("%.2f");QValueAxis *axisY = qobject_cast<QValueAxis *>(chart->axes(Qt::Vertical).at(0));axisY->setRange(0,0.12);axisY->setTitleText("标准差");axisY->setLabelFormat("%.2f");ui->widget->setRenderHint(QPainter::Antialiasing);ui->widget->setChart(chart);int i=0;auto labelsiter=labels.begin();for(auto &&point : data){if(end_flag)return;serieses[*labelsiter]->append(QPointF(point[0],point[1]));i++;labelsiter++;if(i%1000==0){QApplication::processEvents();}}
}void kmeans::on_pushButton_2_clicked()
{end_flag=true;
}
5 最后
🧿 更多资料, 项目分享:
https://gitee.com/dancheng-senior/postgraduate