文章目录
- 行星碰撞
- 机器人碰撞
- 补充题目:2731. 移动机器人
- 参考资料
本文记录了两个使用栈来处理碰撞问题的算法题目。
行星碰撞
https://leetcode.cn/problems/asteroid-collision/
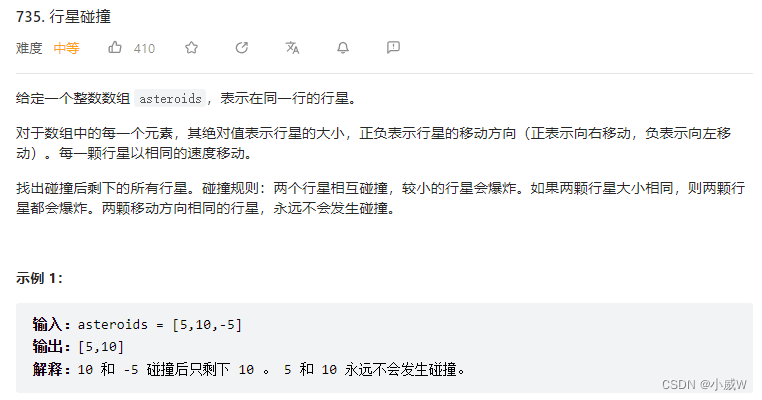
对于这种题目,各个元素分别会向左或向右移动,可以使用栈模拟碰撞的过程。
由于从左往右进行遍历,因此遍历当前元素时,如果它是向右移动的,就只可能会碰撞到它右边还没有被遍历到的元素,因此可以将其直接放入栈中。
当遍历到向左移动的元素时,它只可能碰撞到当前已经在栈中的元素,需要进行一些处理。
class Solution {public int[] asteroidCollision(int[] asteroids) {Deque<Integer> stk = new ArrayDeque();for (int asteroid: asteroids) {if (asteroid > 0) { // 向右移动的直接放入栈中stk.push(asteroid);continue;}boolean f = true; // 记录这个向左的陨石是否还活着while (!stk.isEmpty() && stk.peek() > 0) {if (stk.peek() + asteroid >= 0) {if (stk.peek() + asteroid == 0) stk.pop();f = false; // 被撞死了break;}f = true;stk.pop();}if (f) stk.push(asteroid); // 没被撞死就放入栈中}int n = stk.size(); // 由于下面取元素的时候,栈中元素会不断减少,因此需要提前声明 nint[] ans = new int[n];for (int i = 0; i < n; ++i) ans[n - 1 - i] = stk.pop();return ans;}
}
对于这道题目来说,无非只有三种结果:1.没撞过 2.撞过了 3.同归于尽了。分类写 if 即可。
注意在取出栈中元素的过程中,stk.size() 一直在发生变化,因此代码最后不能写成:
for (int i = 0; i < stk.size(); ++i) ans[stk.size() - 1 - i] = stk.pop();
而必须是事先 通过 int n = stk.size() 接收原始结果中元素的个数。
机器人碰撞
https://leetcode.cn/problems/robot-collisions/
题目出自:第 351 场周赛
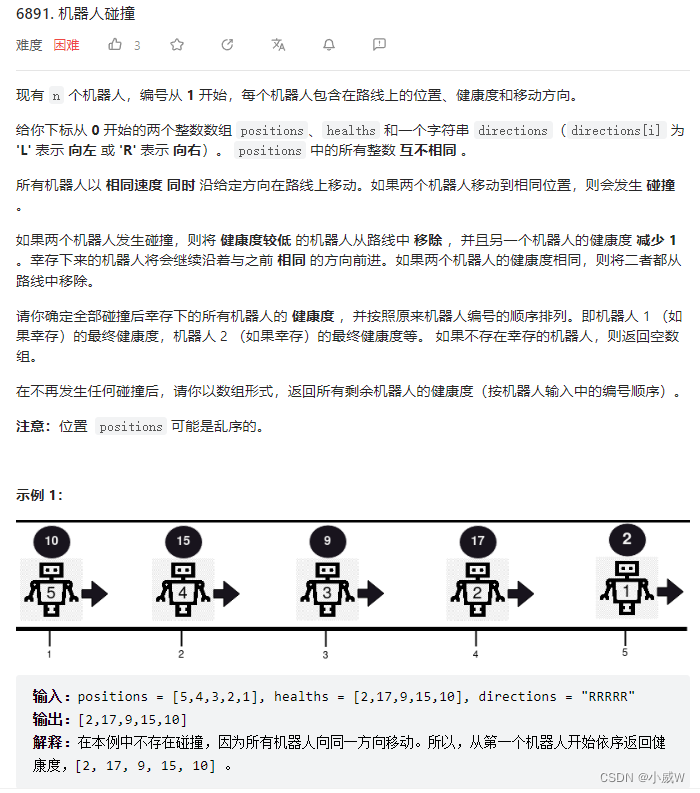
这道题目与 行星碰撞 几乎如出一辙,因此代码模板是一样的,差异几乎只存在于 遍历到向左移动的元素时,处理的方式不同。
class Solution {public List<Integer> survivedRobotsHealths(int[] positions, int[] healths, String directions) {int n = positions.length;Integer[] id = new Integer[n];for (int i = 0; i < n; ++i) id[i] = i; // 记录下标用于排序Arrays.sort(id, (i, j) -> positions[i] - positions[j]); // 按照位置从左往右排序Deque<Integer> stk = new ArrayDeque();for (int i: id) {if (directions.charAt(i) == 'R') { // 向右,加入栈stk.push(i);continue;}while (!stk.isEmpty()) {int top = stk.peek();if (healths[top] > healths[i]) { // 栈顶的健康度大healths[top]--;healths[i] = 0;break;}if (healths[top] == healths[i]) { // 一样大healths[stk.pop()] = 0;healths[i] = 0;break;} // 新来的健康度大healths[stk.pop()] = 0; healths[i]--;// 不需要将向左移动的机器人加入栈,因为如果它撞完了左边向右移动的,就不会再与任何机器人发生碰撞了}}List<Integer> ans = new ArrayList();for (int h: healths) {if (h != 0) ans.add(h);}return ans;}
}
注意由于机器人的 positions 是乱序的,而我们是需要按照位置的从左到右关系进行遍历,因此常用如下操作对下标进行排序。
Integer[] id = new Integer[n];
for (int i = 0; i < n; ++i) id[i] = i; // 记录下标用于排序
Arrays.sort(id, (i, j) -> positions[i] - positions[j]); // 按照位置从左往右排序
之所以声明 Integer[] 而不是 int[] 是因为 在 Java 中 int[] 不支持自定义排序。(关于Java 自定义排序可见:【Java】自定义排序)
注意虽然 int[] 不支持,但 int[][] 是支持的,因为 int[][] 的元素是 int[],已经是引用类型了。
补充题目:2731. 移动机器人
2731. 移动机器人

乍一看这道题目很像是这一类题目,因为两个机器人相撞之后只是改变位置而已,不会对两者的数值或是否存在造成影响。
因此这道题目更像是脑筋急转弯,需要将其相撞转换成——擦肩而过,两者的相撞并不会对结果造成什么影响。既然如此,那么可以把机器人都看成是完全一样的,无法区分。
class Solution {public int sumDistance(int[] nums, String s, int d) {int n = nums.length;final int mod = (int)1e9 + 7;long[] lnums = new long[n];for (int i = 0; i < n; ++i) {lnums[i] = nums[i];if (s.charAt(i) == 'R') lnums[i] += d;else lnums[i] -= d;}Arrays.sort(lnums);long last = 0, ans = 0;for (int i = 1; i < n; ++i) {last = (i * (lnums[i] - lnums[i - 1]) + last) % mod;ans = (ans + last) % mod;}return (int)ans;}
}
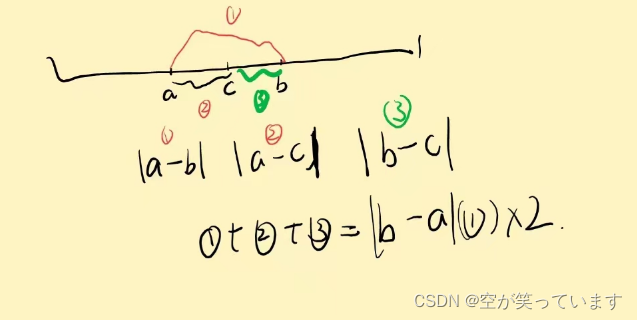
关于机器人之间的两两距离如何计算:

计算时,为了避免溢出,需要取模。(关于取模参见:【算法】数学相关知识总结)
参考资料
栈模拟(Python/Java/C++/Go)