算法动态分析及Java例题讲解-编程知识

动态规划

动态规划（英语：Dynamic programming，简称 DP），是一种在数学、管理科学、计算机科学、经济学和生物信息学中使用的，通过把原问题分解为相对简单的子问题的方式求解复杂问题的方法。动态规划常常适用于有重叠子问题和最优子结构性质的问题。

简单来说，动态规划其实就是，给定一个问题，我们把它拆成一个个子问题，直到子问题可以直接解决。然后呢，把子问题答案保存起来，以减少重复计算。再根据子问题答案反推，得出原问题解的一种方法。

我们可以举一个例子来更好的理解动态规划问题

我们来看下，网上比较流行的一个例子：

★

A ： “1+1+1+1+1+1+1+1 =？”
A ： “上面等式的值是多少”
B ：计算 “8”
A : 在上面等式的左边写上 “1+” 呢？
A : “此时等式的值为多少”
B : 很快得出答案 “9”
A : “你怎么这么快就知道答案了”
A : “只要在8的基础上加1就行了”
A : “所以你不用重新计算，因为你记住了第一个等式的值为8!动态规划算法也可以说是 ‘记住求过的解来节省时间’”

特点

动态规划有几个典型特征，最优子结构、状态转移方程、边界、重叠子问题。

让我们利用下面的例题来分析一下

121. 买卖股票的最佳时机

给定一个数组 prices ，它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。

你只能选择 某一天 买入这只股票，并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。

返回你可以从这笔交易中获取的最大利润。如果你不能获取任何利润，返回 0 。

示例 1：

输入：[7,1,5,3,6,4]
输出：5
解释：在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格；同时，你不能在买入前卖出股票。

示例 2：

输入：prices = [7,6,4,3,1]
输出：0
解释：在这种情况下, 没有交易完成, 所以最大利润为 0。

class Solution {public int maxProfit(int[] prices) {int cost=Integer.MAX_VALUE;int profit=0;   			//边界           for(int price : prices){//最优子机构cost = Math.min(price,cost);profit = Math.max(profit,price-cost);//状态转义方程//每一次的具体遍历就为 重叠子问题}return profit;}
}

LCR 013. 二维区域和检索 - 矩阵不可变

给定一个二维矩阵 matrix，以下类型的多个请求：

计算其子矩形范围内元素的总和，该子矩阵的左上角为 (row1, col1) ，右下角为 (row2, col2) 。

实现 NumMatrix 类：

NumMatrix(int[][] matrix) 给定整数矩阵 matrix 进行初始化
int sumRegion(int row1, int col1, int row2, int col2) 返回左上角 (row1, col1) 、右下角 (row2, col2) 的子矩阵的元素总和。

示例 1：

输入: 
["NumMatrix","sumRegion","sumRegion","sumRegion"]
[[[[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]],[2,1,4,3],[1,1,2,2],[1,2,2,4]]
输出: 
[null, 8, 11, 12]解释:
NumMatrix numMatrix = new NumMatrix([[3,0,1,4,2],[5,6,3,2,1],[1,2,0,1,5],[4,1,0,1,7],[1,0,3,0,5]]]);
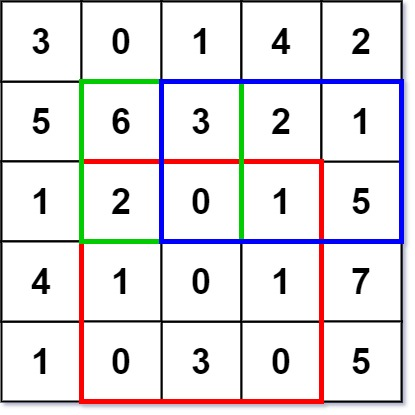
numMatrix.sumRegion(2, 1, 4, 3); // return 8 (红色矩形框的元素总和)
numMatrix.sumRegion(1, 1, 2, 2); // return 11 (绿色矩形框的元素总和)
numMatrix.sumRegion(1, 2, 2, 4); // return 12 (蓝色矩形框的元素总和)

class NumMatrix {int[][] matrixSum;public NumMatrix(int[][] matrix) {matrixSum = new int[matrix.length+1][matrix[0].length+1];//隐含边界 matrixSum[0][i]与matrixSum[i][0]都为0for(int i=1;i<=matrix.length;++i){for(int j=1;j<=matrix[0].length;++j){matrixSum[i][j] = matrixSum[i-1][j]+matrixSum[i][j-1]-matrixSum[i-1][j-1]+matrix[i-1][j-1];//状态转义方程  里面的各个部分就为最优子结构}}}public int sumRegion(int row1, int col1, int row2, int col2) {return matrixSum[row2+1][col2+1] - matrixSum[row1-1+1][col2+1] - matrixSum[row2+1][col1-1+1]+matrixSum[row1-1+1][col1-1+1];}
}/*** Your NumMatrix object will be instantiated and called as such:* NumMatrix obj = new NumMatrix(matrix);* int param_1 = obj.sumRegion(row1,col1,row2,col2);*/