题目描述
观察下面的数字金字塔。写一个程序查找从最高点到底部任意处结束的路径,使路径经过数字的和最大。每一步可以从当前点走到左下方的点也可以到达右下方的点。
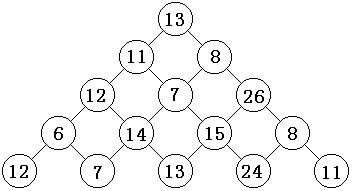
在上面的样例中,从13到8到26到15到24的路径产生了最大的和86。
输入
第一个行包含R(1≤ R≤1000),表示行的数目。
后面每行为这个数字金字塔特定行包含的整数。
所有的被供应的整数是非负的且不大于100。
输出
单独的一行,包含那个可能得到的最大的和。
样例输入1
5
13
11 8
12 7 26
6 14 15 8
12 7 13 24 11
样例输出1
86
提示/说明
标签
普及 其他 递归 递推 记忆化搜索 动态规划基础
方法一:
暴搜
时间超限67
方法二:
顺推
动规
状态转移方程:
向左走:f[i+1][j]>f[i][j]+a[i+1][j]?f[i+1][j]:f[i][j]+a[i+1][j]
向右走:f[i+1][j+1]>f[i][j]+a[i+1][j+1]?f[i+1][j+1]:f[i][j]+a[i+1][j+1]
代码:
#include<iostream>
using namespace std;
#define MAXN 1010
int a[MAXN][MAXN],f[MAXN][MAXN];
int n;
int main(){cin>>n;for(int i=0;i<n;i++){for(int j=0;j<i+1;j++){cin>>a[i][j];}}f[0][0]=a[0][0];for(int i=0;i<n-1;i++){for(int j=0;j<i+1;j++){f[i+1][j]=f[i+1][j]>f[i][j]+a[i+1][j]?f[i+1][j]:f[i][j]+a[i+1][j];f[i+1][j+1]=f[i+1][j+1]>f[i][j]+a[i+1][j+1]?f[i+1][j+1]:f[i][j]+a[i+1][j+1];}}int ans=f[n-1][0];for(int i=1;i<n;i++){ans=ans>f[n-1][i]?ans:f[n-1][i];}cout<<ans;return 0;
}方法三:逆推
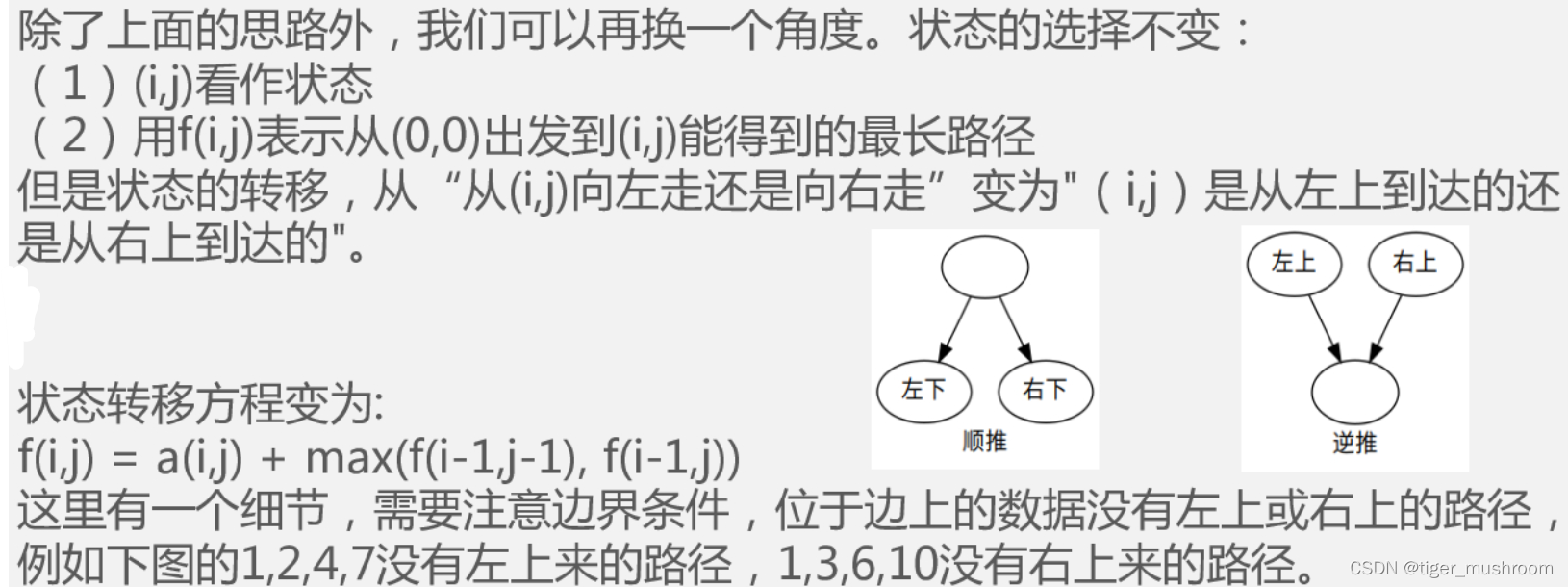
#include<iostream>
using namespace std;
int n;
int a[1005][1005],f[1005][1005];
int main(){cin>>n;for(int i=0;i<n;i++){for(int j=0;j<i+1;j++){cin>>a[i][j];}}for(int i=0;i<n;i++){f[n-1][i]=a[n-1][i];}for(int i=n-2;i>=0;i--){for(int j=0;j<i+1;j++){f[i][j]=a[i][j]+(f[i+1][j]>f[i+1][j+1]?f[i+1][j]:f[i+1][j+1]);}}cout<<f[0][0];return 0;
}方法四:记忆化搜索
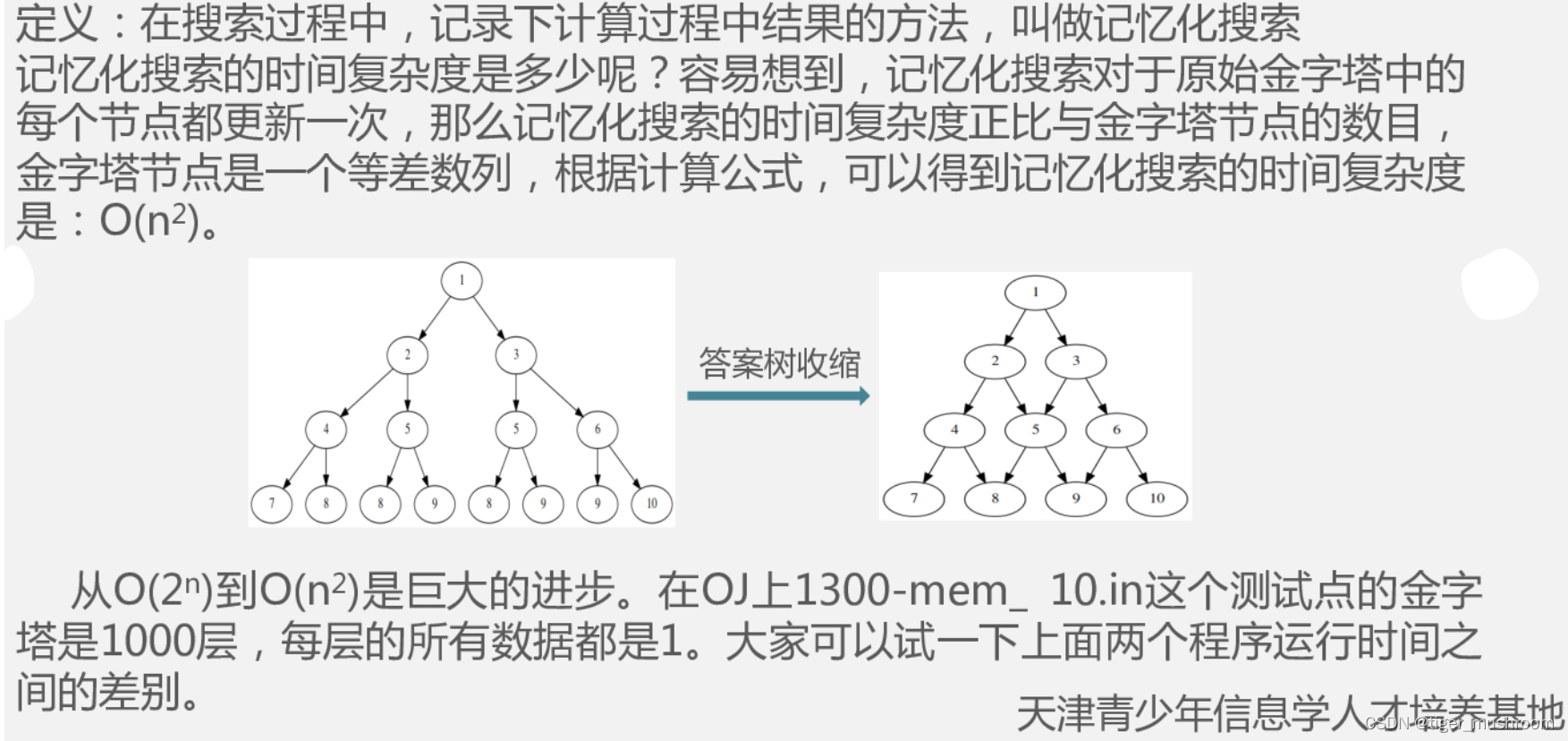
#include<bits/stdc++.h>
#define maxx 1005
using namespace std;
int r,a[maxx][maxx],f[maxx][maxx];
int dfs(int x,int y){if(f[x][y]>=0) return f[x][y];if(x==r) f[x][y]=a[x][y];else f[x][y]=max(dfs(x+1,y),dfs(x+1,y+1))+a[x][y];return f[x][y];
}
int main(){cin>>r;for(int i=1;i<=r;i++){for(int j=1;j<=i;j++){cin>>a[i][j];}}memset(f,-1,sizeof(f));cout<<dfs(1,1)<<'\n';return 0;
}