Doherty理论—理想架构的Doherty功率放大器理论与仿真

参考：
三路Doherty设计
01 射频基础知识–基础概念

ADS仿真工程文件链接：理想架构的Doherty功率放大器理论与仿真

0、Doherty架构的作用

Doherty功放是一种利用负载调制技术提高回退效率的功放，其应用背景是为了解决通信系统中调制信号峰均比越来越大，而传统放大器在功率回退点效率低的问题。

为了提高通讯系统的频谱利用率，为用户提供快速的数据传输和多媒体数据业务以及全球漫游功能，现在的通讯系统采用宽带的数字调制技术，如BPSK、QPSK和QAM等，其峰均比（PAPR）都较高。

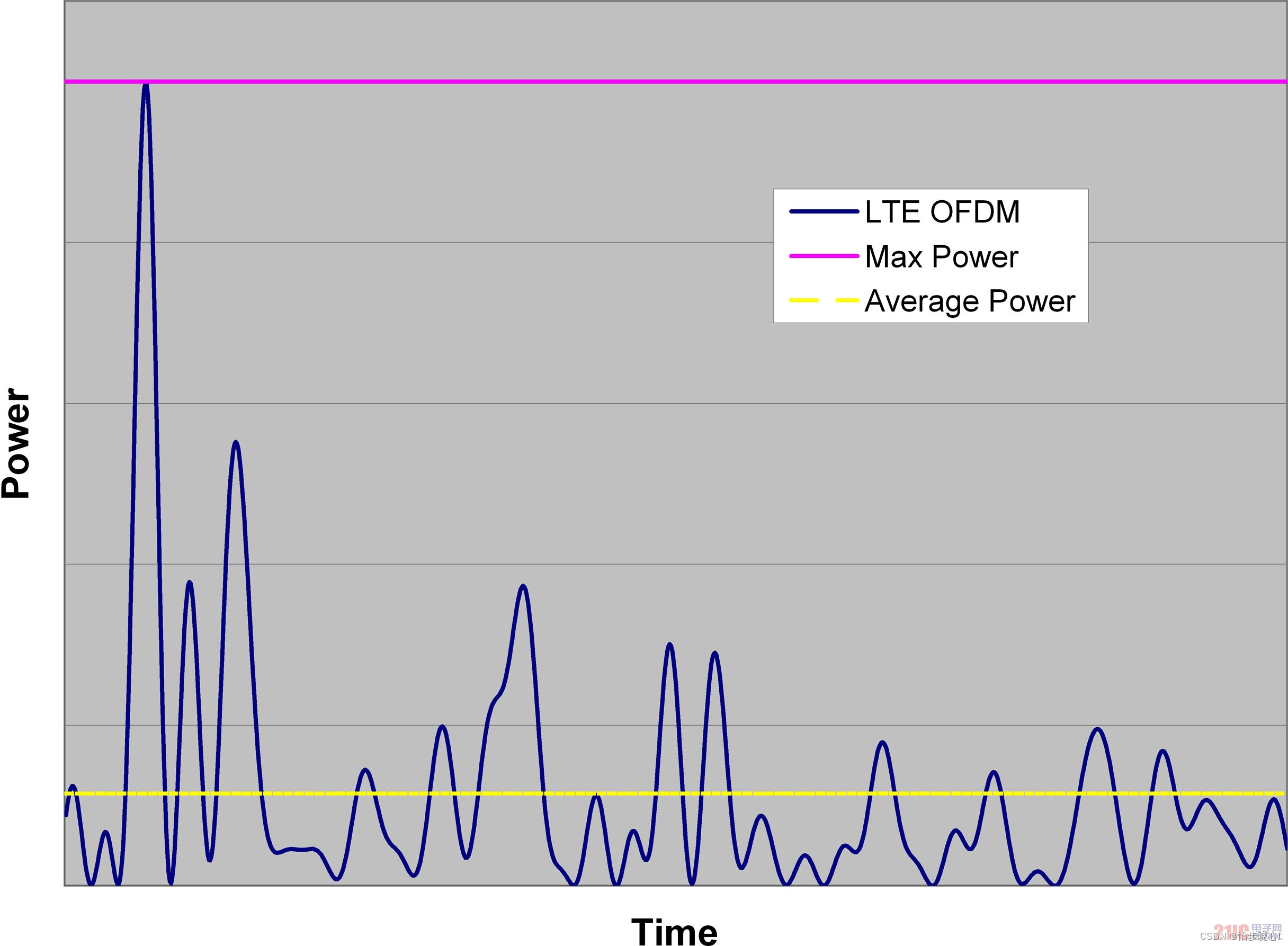
峰均比是啥意思呢，就是峰值功率和平均功率的比值，比如下面这个OFDM的时域信号，由于信号高低不平，峰值功率和平均功率差异较大。假如峰值功率是40dbm，而平均功率是32.5dbm，那么这个信号的峰均比就是40-32.5=7.5dbm。

高峰均比对功率放大器的设计提出了更高的要求，我们都知道功放在饱和时效率较高，B类最高可到78.5%的效率。假设有一个B类功放饱和时输出功率40dbm，效率78.5%，那么如果使用PAPR是7.5dB的调制信号，为了同时保证峰值不失真，这个功放在大部分时间的输出功率就是32.5dBm，那么其在32.5dBm输出时的效率是多少呢？我们使用ADS仿真得到结果（仿真文件在最上方链接）：

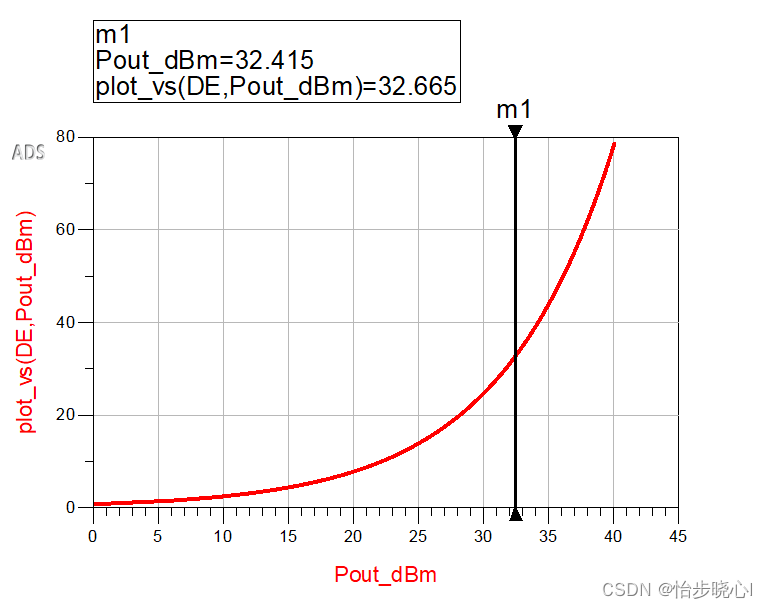
由此可见，为了同时保证峰值和均值的不失真，功率放大器大部分时间都工作在回退状态，但是普通单管功放在回退状态下效率下降快，效率低，由此能耗大不实用。

Doherty技术、Cherix技术（Outphasing异相）、EER（envelope elimination and restoration）和包络跟踪技术ER都是为了解决这一问题。

其中Doherty技术在基站功放运用最广；EER和ER效率高，但是受制于对电源带宽的要求，往往运用在手机等小功率的功放中。

1、经典Doherty架构

1.1、经典Doherty结构

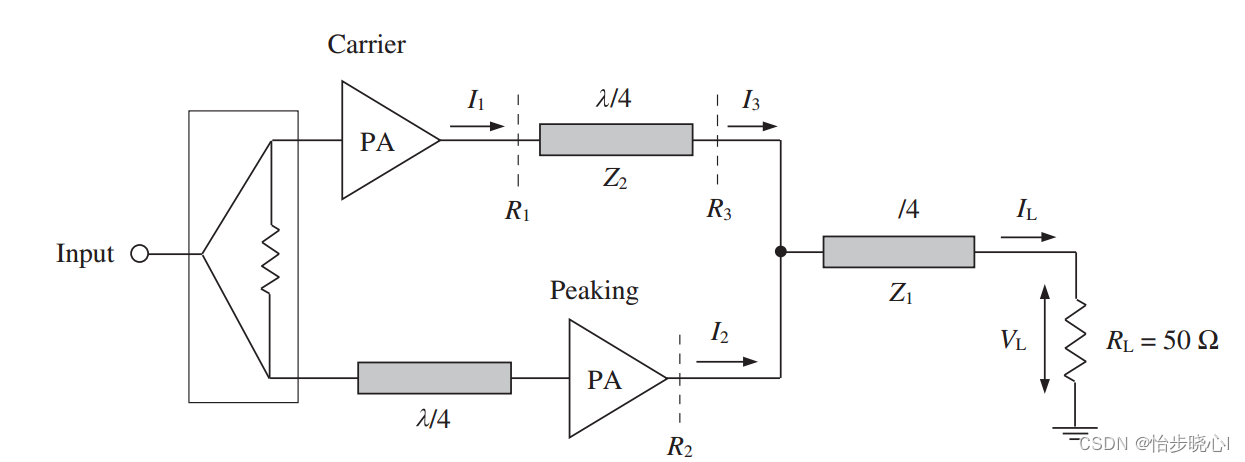
咋参考Switchmode RF and Microwave Power Amplifiers里面的图片，Z2的阻抗为Ropt（B类最佳基波阻抗），Z1是四分之一波长阻抗变换器，将Ropt/2的阻抗变换为50欧姆，因此其阻抗为(Ropt/2*50)^0.5欧姆。至于峰值功放前的四分之一波长线，那个是相位延迟的，因为载波功放那边有一个四分之一波长线了，为了让合路的相位一致，必须也要在峰值功放加上一个。

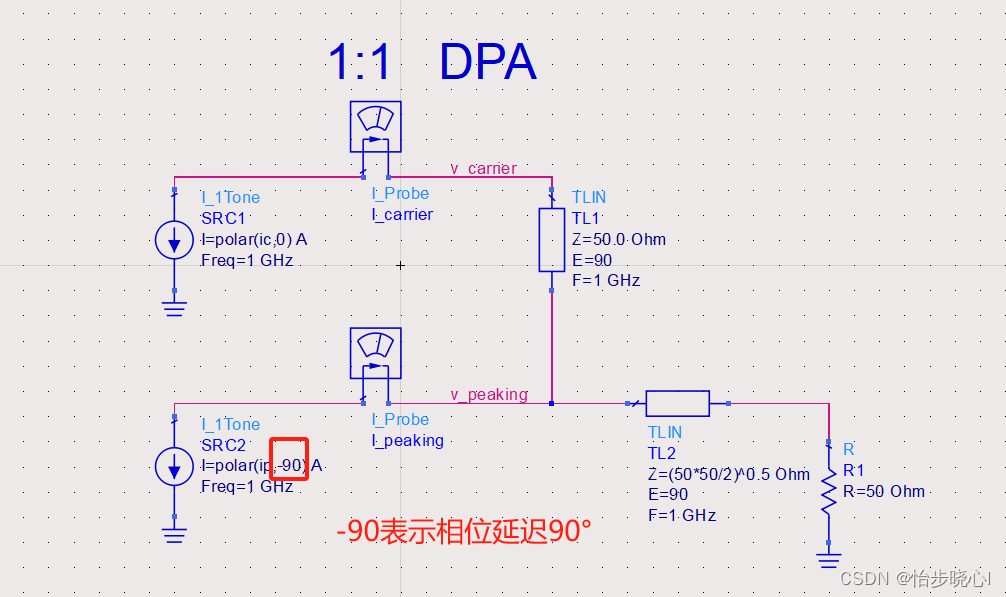
直接讲理论可能比较难，先在ADS中仿真一下：

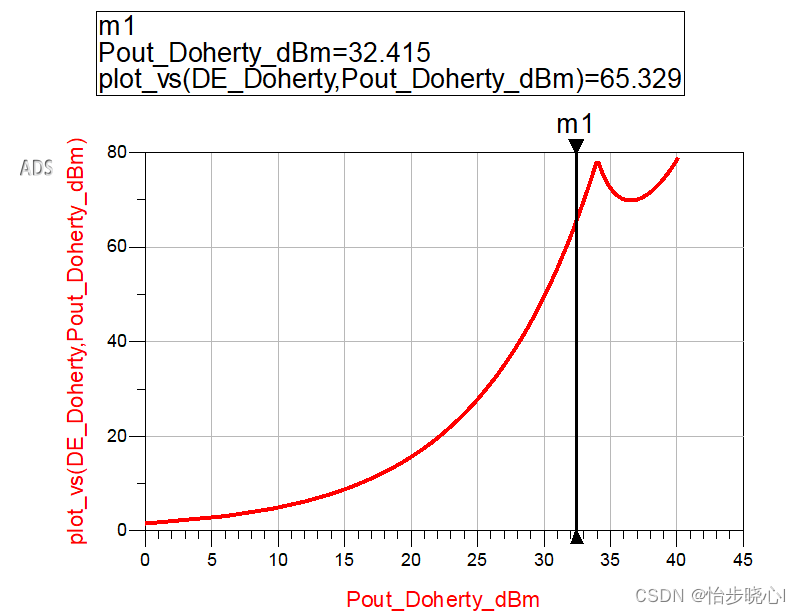
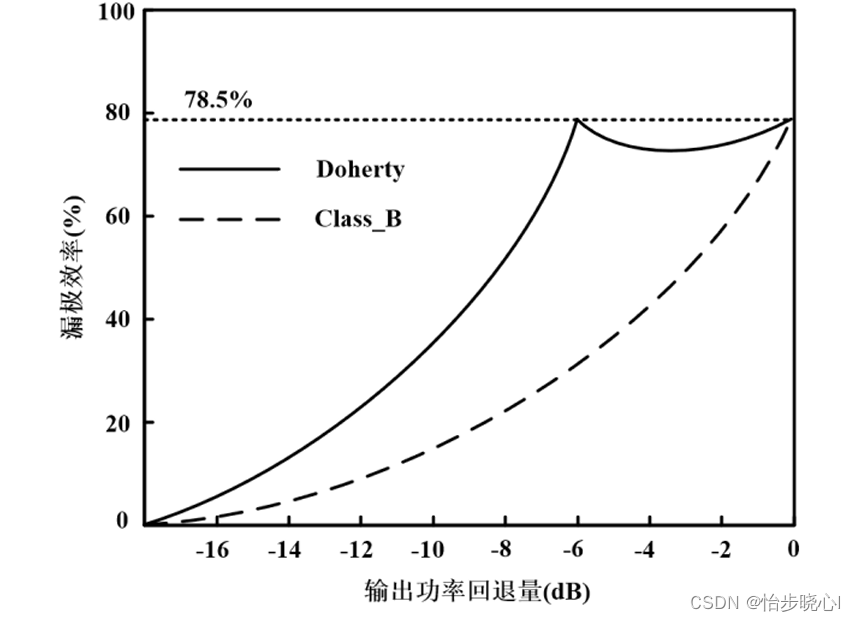
1.2、经典Doherty效率曲线

对上面结构进行仿真，可以看到，在6dB回退的时候效率再次达到最高78.5%，在7.5dB回退的时候，效率高达65.3%，非常的yes了：

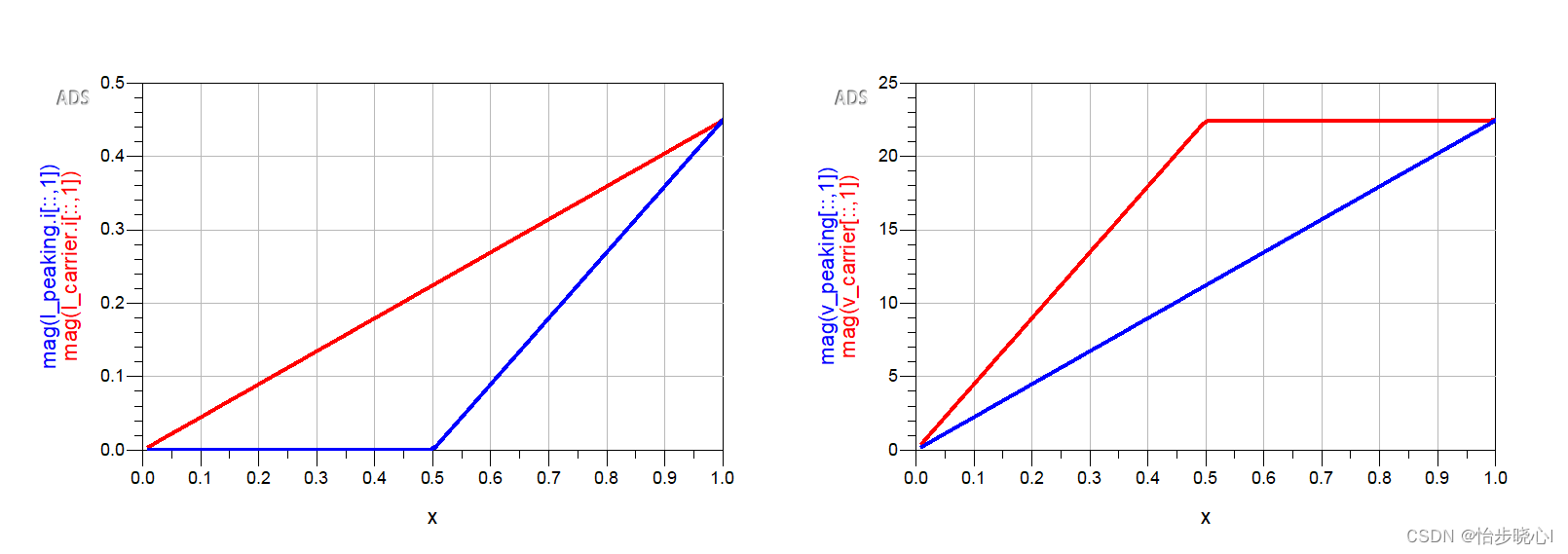
1.3、经典Doherty的输出电压、电流

观察峰值功放和载波功放的电压电流，由于是1：1等分的，在饱和时峰值功放和载波功放的输出功率相同，输出电压、电流也一致，如下所示：

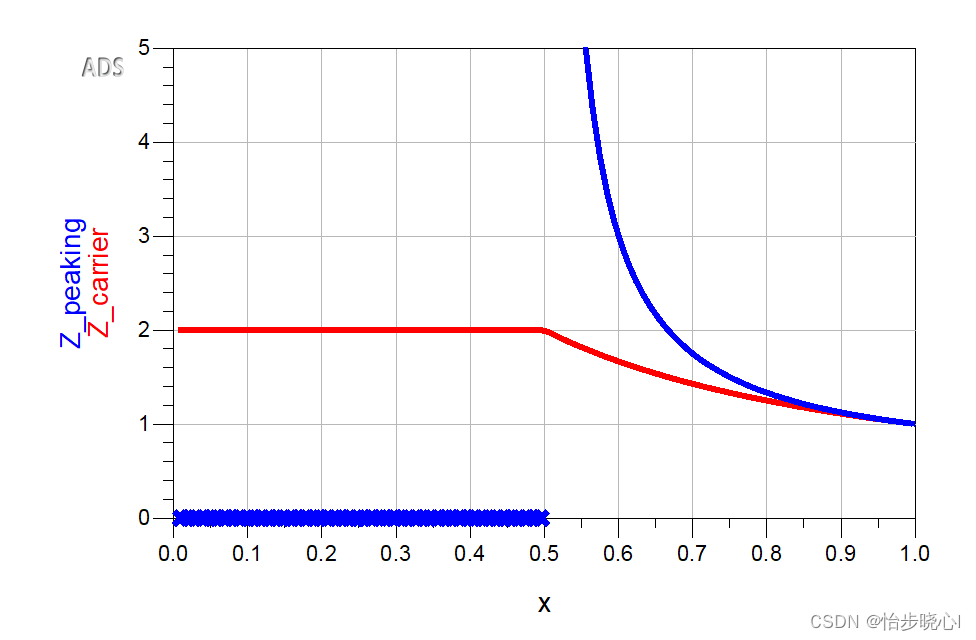
1.4、经典Doherty的输出阻抗关系

观察峰值功放和载波功放的输出阻抗变化，由此可见峰值功放的输出阻抗从无穷大逐渐下降到Ropt，而载波功放的输出阻抗在峰值功放关闭时为2Ropt，在峰值功放打开后逐渐降为Ropt：

2、经典Doherty架构的理论推导过程

参考：应用于5G通信系统高效率射频功率放大器的研究
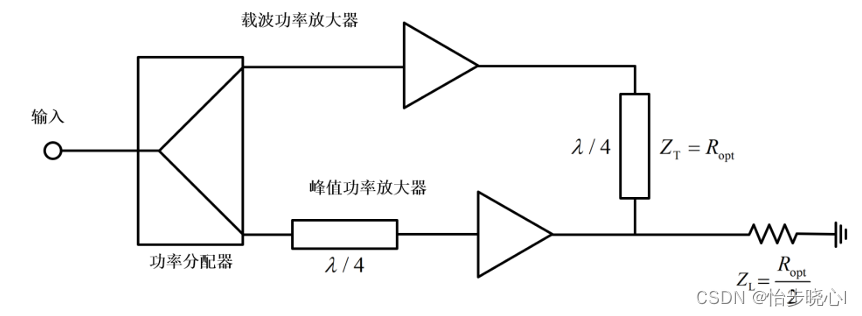
Doherty功放原理图如下，由功率分配器、工作模式为B类（或AB类）的载波功放、工作模式为C类的峰值功放以及功率合成网络组成，输出负载阻抗为Ropt/2（1.1的架构输出阻抗是50欧姆，因此多了四分之一波长微带线进行阻抗变换，把Ropt/2变换到50欧姆）

2.1、低功率状态

下图为Doherty功放在低功率工作状态的电路拓扑图，经功率分配器流入峰值功放的射频信号功率未能将其开启，仅载波功放启动工作（峰值功放不工作，那边是断开的）：

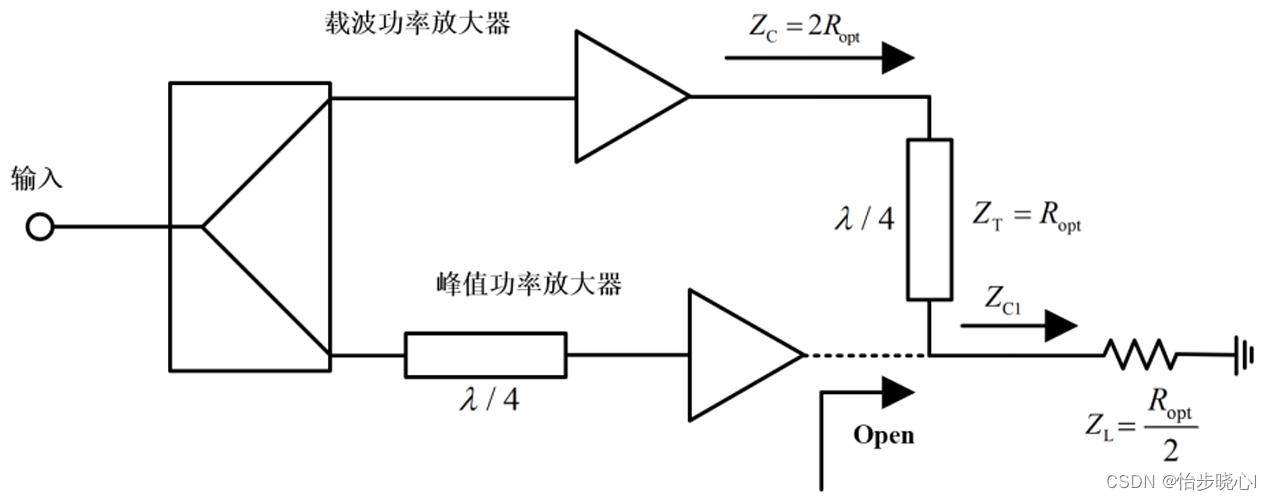
载波功放的负载阻抗为（ZL通过四分之一波长线进行变换，得到2Ropt）：
$$Z_{\mathrm{C}}=\frac{Z_{\mathrm{T}}}{Z_{\mathrm{L}}}=2R_{\mathrm{opt}}$$

此时载波功放为高阻抗状态，电压提前饱和达到Vmax。为什么负载阻抗2Ropt会使得电压提前饱和呢？我初学时也考虑过这个问题，这是因为GAN晶体管实际上是压控电流源，在固定栅极输入情况下，其输出电流是恒定的，此时增加负载阻抗从Ropt到2Ropt，那么根据欧姆定律V=IR，R=2Ropt，那么I会在峰值电流一半的时候电压就饱和了， 1.3小节的仿真图像中也能看出这一点。

由于电流仅达到饱和值的一半，因此该未饱和功率值为：
$$P_{{\mathrm{OBO}}_{-}2R_{\mathrm{opt}}}=\frac{1}{2}{I}_1\cdot V_1=\frac{1}{4}{I}_{\max }{V}_{\mathrm{dc}}$$

也就是峰值功放单独工作时其输出功率为DPA架构极限输出功率的四分之一，也就是传统DPA具有6dB的回退区间。

2.2、高功率状态

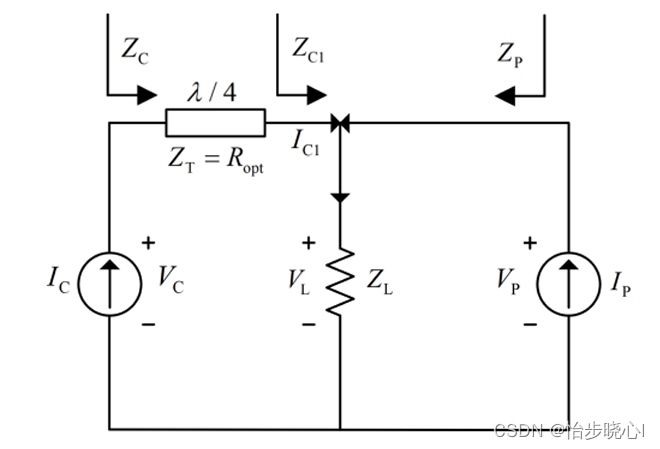
下图为Doherty功放在高功率工作状态的等效电路图。随着输入功率的不断增大，峰值功率放大器逐渐开启并触发有源负载调制直至两路功放均达到饱和输出状态。

对于对称型Doherty功放，假设$\xi (0\le \xi \le 1)$为回退因数，则两路功放电流值分别为：
$$\{\begin{array}{rl}{I}_{\mathrm{C}}& =\frac{I_{\max }}{4}(1+\xi )\\ I_{\mathrm{p}}& =\frac{I_{\max }}{2}\xi \end{array}$$
当两路功放电流饱和（$\xi =1$）时，可以得到：
$$\begin{array}{rl}{Z}_{\mathrm{C}}& =Z_{\mathrm{P}}=R_{\mathrm{opt}}\\ & \\ V_{\mathrm{C}}& =V_{\mathrm{P}}=\frac{I_{\max }}{2}\cdot R_{\mathrm{opt}}\end{array}$$
基波电流在两路功放输出端分别为$I_c$和$I_{c1}$，在信号合路处两端的有效负载分别为：
$$\begin{array}{rl}{Z}_{C1}& =Z_{\mathrm{L}}(1+\frac{I_{\mathrm{p}}}{I_{C1}})=\frac{R_{\mathrm{opt}}}{2}(1+\frac{I_{\mathrm{p}}}{I_{C1}})\\ & \\ Z_{\mathrm{C}}& =Z_{\mathrm{L}}(1+\frac{I_{C1}}{I_{\mathrm{P}}})=\frac{R_{\mathrm{opt}}}{2}(1+\frac{I_{C1}}{I_{\mathrm{P}}})\end{array}$$
通过四分之一波长阻抗逆变线的两端电流电压特性可知：
$$Z_{\mathrm{T}}=\frac{V_{\mathrm{C}}}{I_{C1}}$$
由上面两个式子可得：
$$Z_{C1}=\frac{R_{\mathrm{opt}}}{2}(1+\frac{I_{\mathrm{p}}\cdot Z_{\mathrm{T}}}{V_{\mathrm{C}}})=\frac{R_{\mathrm{opt}}}{2}(1+\frac{I_{\mathrm{P}}\cdot R_{\mathrm{opt}}}{V_{\mathrm{C}}})$$

对于四分之一波长阻抗逆变线，存在如下阻抗变换关系：
$$Z_{\mathrm{C}}=\frac{Z_{\mathrm{T}}^2}{Z_{C1}}=\frac{R_{\mathrm{opt}}^2}{Z_{C1}}$$

联立上面两个公式，可得：
$$Z_{\mathrm{C}}=\frac{2{Z_{\mathrm{T}}}^2}{R_{\mathrm{opt}}\left(1+\frac{I_{\mathrm{p}}\cdot R_{\mathrm{opt}}}{V_{\mathrm{C}}}\right)}$$
$$V_{\mathrm{C}}=\frac{I_{\max }}{2}\cdot R_{\mathrm{opt}}$$

由式（2.46）可知，在大功率状态$V_C$不受回退因数$\xi$的影响，电压在电流变化时仍能保持峰值状态，由此得到的理论结果如下所示（和上面仿真的一致）：

2.3、理论输出阻抗计算

下式也可以用来确定载波功放的输出阻抗：$$Z_{\mathrm{C}}=\frac{2{Z_{\mathrm{T}}}^2}{R_{\mathrm{opt}}\left(1+\frac{I_{\mathrm{p}}\cdot R_{\mathrm{opt}}}{V_{\mathrm{C}}}\right)}$$

当峰值功放没有开启时，$I_{\mathrm{p}}=0$，由此：
$$Z_{\mathrm{C}}=\frac{2{Z_{\mathrm{T}}}^2}{R_{\mathrm{opt}}\left(1+\frac{I_{\mathrm{p}}\cdot R_{\mathrm{opt}}}{V_{\mathrm{C}}}\right)}=2R_{\mathrm{opt}}$$

当峰值功放饱和时，$I_{\mathrm{p}}=V_C/R_{opt}$，由此：
$$Z_{\mathrm{C}}=\frac{2{Z_{\mathrm{T}}}^2}{R_{\mathrm{opt}}\left(1+\frac{I_{\mathrm{p}}\cdot R_{\mathrm{opt}}}{V_{\mathrm{C}}}\right)}=R_{\mathrm{opt}}$$

---

当峰值功放没有开启时，$I_{\mathrm{p}}=0$，由此R=V/I，峰值功放输出阻抗无穷大。

当峰值功放饱和时$Z_{\mathrm{C}}=Z_{\mathrm{P}}=R_{\mathrm{opt}}$，由此可以画图：