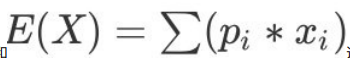当我们柱状图中X轴数据太多的时候,会自动把柱形的宽度挤的很细,带来的交互非常不好,我们可以用dataZoom属性来解决
简易的版本,横向滚动。
option.dataZoom = [{type: "slider",show: true,startValue: 0, //数据窗口范围的起始百分比endValue: 8,},
];效果如下:

如果需要自动滚动,需要再加个定时器,
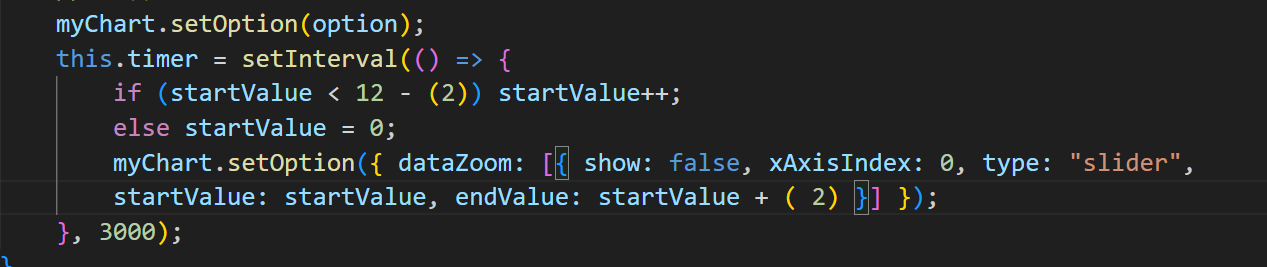
还可以在标签上设置鼠标放上去停止滚动
@mouseover="hovers = true" @mouseleave="hovers = false"