【数据结构】二叉搜索树的模拟实现-编程知识

1、概念

2、模拟实现

2.1、查找

2.2、插入

2.3、删除（难点）

3、性能分析

4、完整代码

1、概念

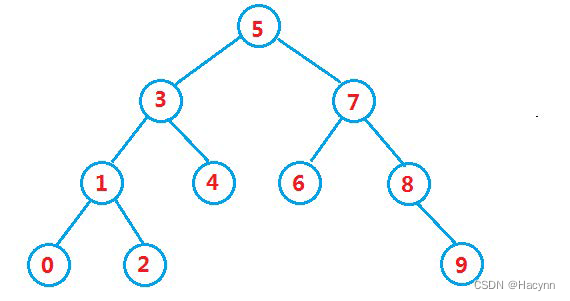
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树:

若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
它的左右子树也分别为二叉搜索树

Java底层实现搜索树的两个主要类是TreeSet和TreeMap。

        TreeSet是基于红黑树（Red-Black tree）实现的，它提供了对元素的唯一性排序。TreeSet中的元素是唯一的，并且按照升序排序。

        TreeMap也是基于红黑树实现的，它提供了一个键值对的映射关系，并且按照键的升序排序。TreeMap允许使用null键和null值。

        这两个类都实现了NavigableMap和SortedMap接口，提供了更丰富的方法用于搜索、排序和遍历操作。

        为了更好的理解TreeSet和TreeMap的使用以及底层原理，下面带大家模拟实现一下搜索树。

2、模拟实现

2.1、查找

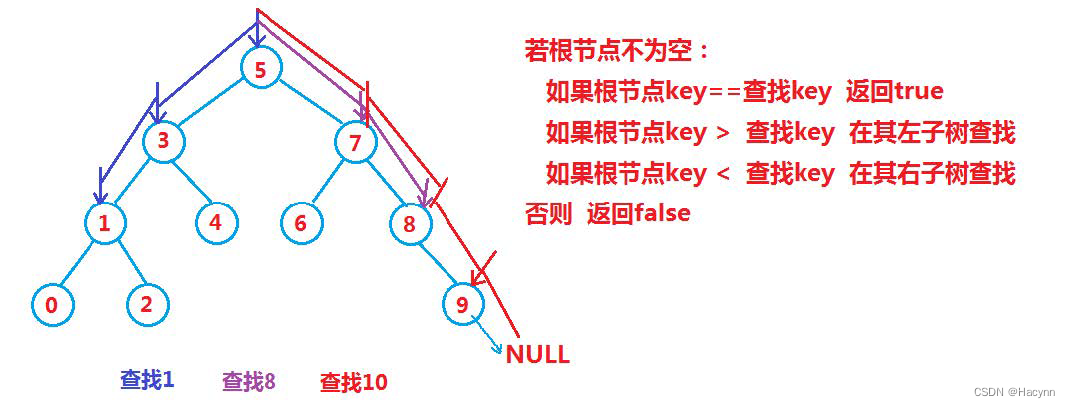
若根节点不为空：

如果根节点key==查找key，返回true
如果根节点key > 查找key，去其左子树上查找
如果根节点key < 查找key，去其右子树上查找

否则返回false

    public boolean search(int val) {TreeNode cur = root;while (cur != null) {if (cur.val > val) {   //当前节点大于val，去左子树上继续找cur = cur.left;} else if (cur.val < val) {   //当前节点小于val，去右子树上继续找cur = cur.right;} else {return true;   //找到返回true}}return false;}

2.2、插入

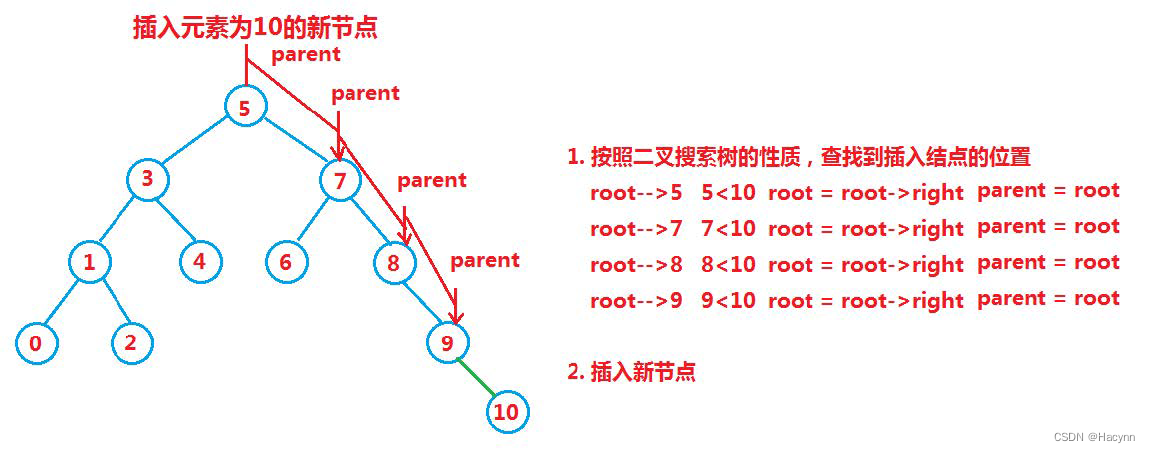
插入时分为两种大情况：树为空以及树不为空

1、如果树为空树，即根 == null，直接插入

2、如果树不是空树，按照查找逻辑确定插入位置，插入新结点

    public void insert(int val) {if (root == null) {    //树为空时直接插入并返回root = new TreeNode(val);return;}TreeNode cur = root;TreeNode prev = null;    //指向cur前一个节点（即父亲节点），用于最终插入时使用while (cur != null) {prev = cur;      //更新prev指向if (cur.val > val) {cur = cur.left;} else if (cur.val < val) {cur = cur.right;} else {return;  //遇到相同退出,无需重复插入}}if (prev.val > val) {    //判断插入的正确位置prev.left = new TreeNode(val);} else {prev.right = new TreeNode(val);}}

2.3、删除（难点）

删除操作是二叉搜索树三种基本操作中最难的一个操作，它的难点不在于代码的难度，而是因为涉及到的情况居多，稍微不注意就容易漏判断某一条情况，因此使用合理的思路去理解记忆二叉搜索树的删除操作是非常必要的。

设待删除结点为 cur, 待删除结点的双亲结点为 prev。对cur删除节点的三种情况进行分析：

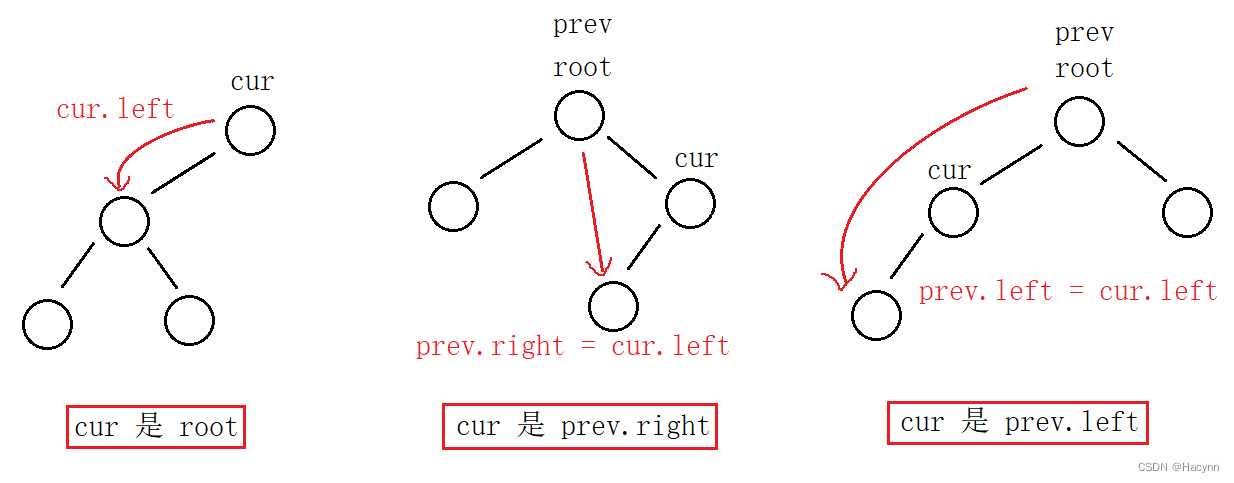
1. cur.left == null

cur 是 root，则 root = cur.right
cur 不是 root，cur 是 prev.left，则 prev.left = cur.right
cur 不是 root，cur 是 prev.right，则 prev.right = cur.right

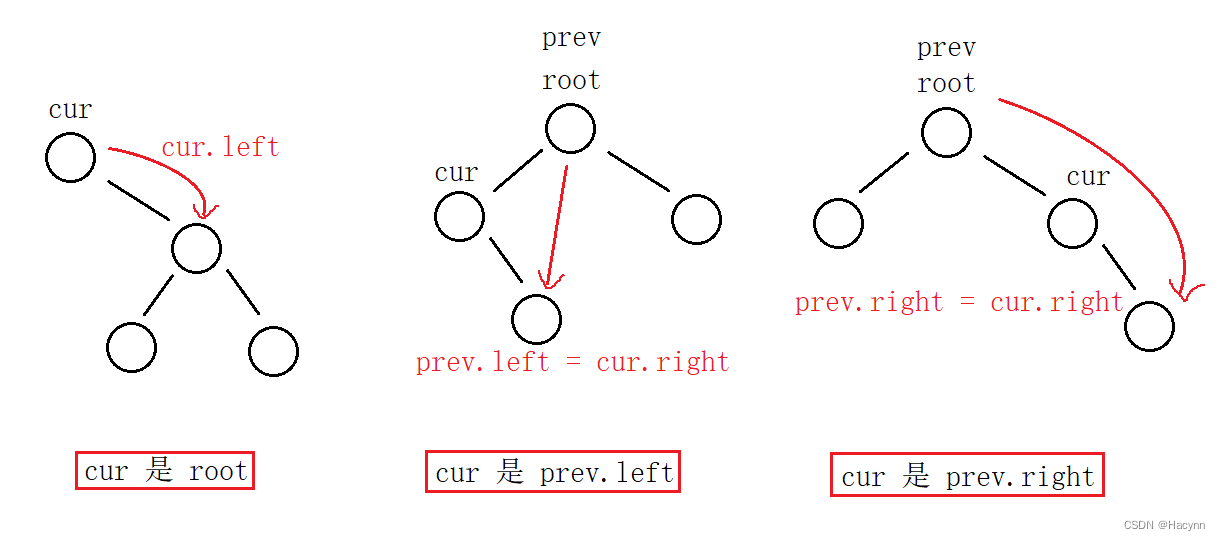
2. cur.right == null

cur 是 root，则 root = cur.left
cur 不是 root，cur 是 prev.left，则 prev.left = cur.left
cur 不是 root，cur 是 prev.right，则 prev.right = cur.left

3. cur.left != null && cur.right != null

需要使用替换法进行删除。

替换法的核心是：找到删除节点左子树中的最大值（即子树中的最右节点，这个节点一定没有右右子树），或者删除节点右子树中的最小值（即子树中的最左节点，这个节点一定没有左子树），用它的值填补到被删除节点中，再来处理该结点的删除问题。

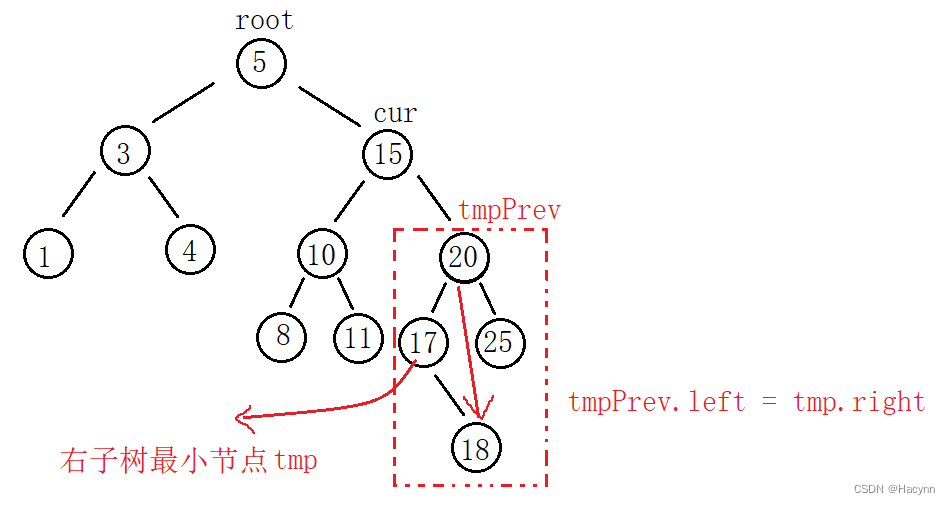
以下讲解使用替换删除节点右子树的最小节点：

首先找到最小节点tmp，以及最小节点的父亲tmpPrev，如图所示结构，紧着cur.val = tmp.val替换值，然后删除tmp节点，删除步骤如图所示，即tmpPrev.left = tmp.right。

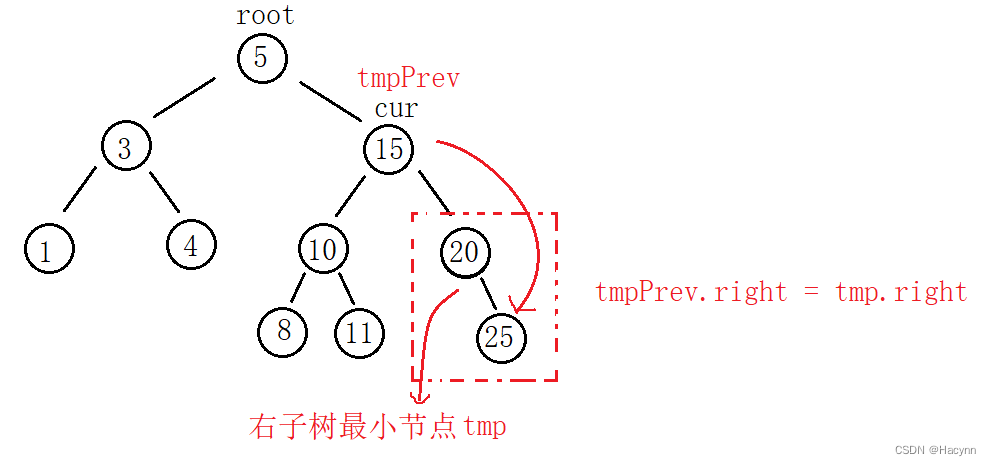
值得注意的是，有一种情况会被忽略，即当cur.right 节点无左子树时，此时tmpPrev仍然是cur，而tmp即为cur.right，此时删除tmp节点的步骤就变为了tmpPrev.right = tmp.right

    public void remove(int val) {TreeNode cur = root;TreeNode prev = null;while (cur != null) {prev = cur;if(cur.val > val) {cur = cur.left;} else if (cur.val < val){cur = cur.right;} else {removeNode(cur,prev);return;}}}public void removeNode(TreeNode cur, TreeNode prev) {if(cur.left == null) {if(cur == root) {root = cur.right;} else if (prev.left == cur) {prev.left = cur.right;} else {prev.right = cur.right;}} else if (cur.right == null) {if(cur == root) {root = cur.left;} else if (prev.left == cur) {prev.left = cur.left;} else {prev.right = cur.left;}} else {TreeNode tmp = cur.right;TreeNode tmpPrev = cur;while(tmp.left != null) {tmpPrev = tmp;tmp = tmp.left;}cur.val = tmp.val;//注意，可能没有进入while循环，此时这里的两种情况if (tmpPrev.left == tmp) {tmpPrev.left = tmp.right;} else {tmpPrev.right = tmp.right;}}}

3、性能分析

插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：

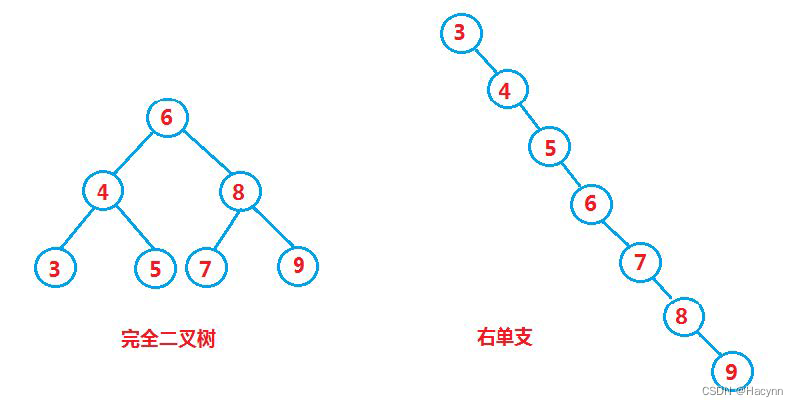
最优情况下，二叉搜索树为完全二叉树，其平均比较次数为： $\log_{2}N$

最差情况下，二叉搜索树退化为单支树，其平均比较次数为： $\frac{N}{2}$

如果退化成单支树，二叉搜索树的性能就失去了，而为了改进这一缺陷，就有了AVL树。

AVL树是最先发明的自平衡二叉搜索树。在AVL树中任何节点的两个子树的高度最大差别为1，所以它也被称为高度平衡树。增加和删除可能需要通过一次或多次树旋转来重新平衡这个树。

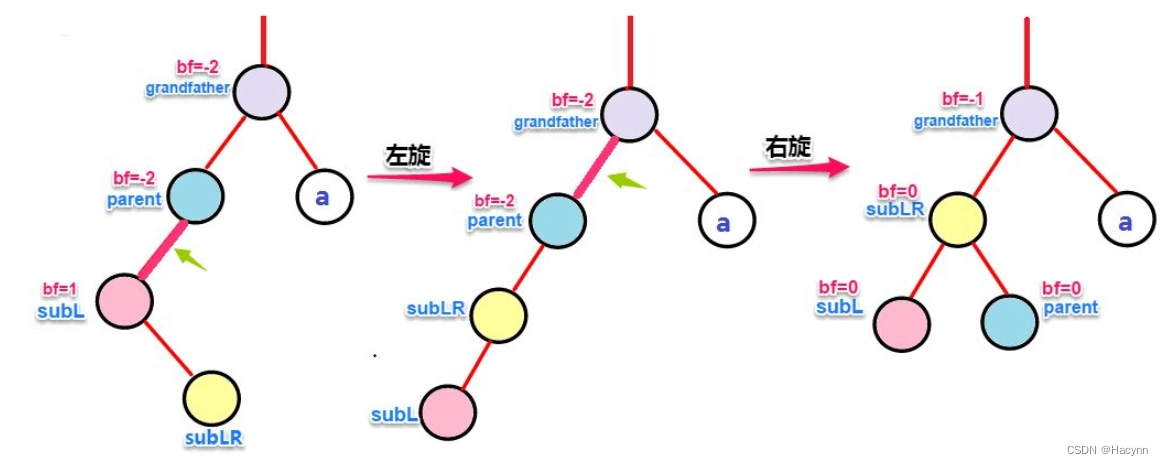
本篇博客的重点不在AVL树上，因此不对AVL树进行展开讲解，可自行搜索了解。

4、完整代码

package BinarySearchTree;public class BinarySearchTree {static class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}}public TreeNode root;public boolean search(int val) {TreeNode cur = root;while (cur != null) {if (cur.val > val) {cur = cur.left;} else if (cur.val < val) {cur = cur.right;} else {return true;}}return false;}public void insert(int val) {if (root == null) {root = new TreeNode(val);return;}TreeNode cur = root;TreeNode prev = null;while (cur != null) {prev = cur;if (cur.val > val) {cur = cur.left;} else if (cur.val < val) {cur = cur.right;} else {return;  //相同退出}}if (prev.val > val) {prev.left = new TreeNode(val);} else {prev.right = new TreeNode(val);}}public void remove(int val) {TreeNode cur = root;TreeNode prev = null;while (cur != null) {prev = cur;if(cur.val > val) {cur = cur.left;} else if (cur.val < val){cur = cur.right;} else {removeNode(cur,prev);return;}}}public void removeNode(TreeNode cur, TreeNode prev) {if(cur.left == null) {if(cur == root) {root = cur.right;} else if (prev.left == cur) {prev.left = cur.right;} else {prev.right = cur.right;}} else if (cur.right == null) {if(cur == root) {root = cur.left;} else if (prev.left == cur) {prev.left = cur.left;} else {prev.right = cur.left;}} else {TreeNode tmp = cur.right;TreeNode tmpPrev = cur;while(tmp.left != null) {tmpPrev = tmp;tmp = tmp.left;}cur.val = tmp.val;//注意当没有进入while循环时这里的两种情况if (tmpPrev.left == tmp) {tmpPrev.left = tmp.right;} else {tmpPrev.right = tmp.right;}}}
}

【博主推荐】

【LeetCode力扣】面试题 17.14. 最小K个数（top-k问题）-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/135737266?spm=1001.2014.3001.5501【LeetCode力扣】42. 接雨水-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134104222?spm=1001.2014.3001.5501【LeetCode力扣】189 53 轮转数组 | 最大子数组和-CSDN博客https://blog.csdn.net/zzzzzhxxx/article/details/134095703?spm=1001.2014.3001.5501