目录

329. 矩阵中的最长递增路径 Longest Increasing Path In A Matrix  🌟🌟

330. 按要求补齐数组 Patching Array  🌟🌟

🌟 每日一练刷题专栏 🌟

Rust每日一练 专栏

Golang每日一练 专栏

Python每日一练 专栏

C/C++每日一练 专栏

Java每日一练 专栏

---

329. 矩阵中的最长递增路径 Longest Increasing Path In A Matrix

给定一个 m x n 整数矩阵 matrix ，找出其中 最长递增路径 的长度。

对于每个单元格，你可以往上，下，左，右四个方向移动。 你 不能 在 对角线 方向上移动或移动到 边界外（即不允许环绕）。

示例 1：

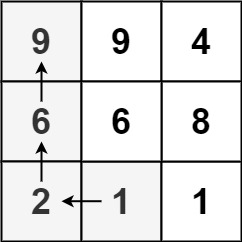
输入：matrix = [[9,9,4],[6,6,8],[2,1,1]]
输出：4 
解释：最长递增路径为 [1, 2, 6, 9]。

示例 2：

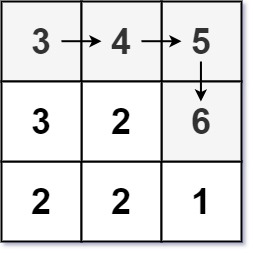
输入：matrix = [[3,4,5],[3,2,6],[2,2,1]]
输出：4 
解释：最长递增路径是 [3, 4, 5, 6]。注意不允许在对角线方向上移动。

示例 3：

输入：matrix = [[1]]
输出：1

提示：

• m == matrix.length
• n == matrix[i].length
• 1 <= m, n <= 200
• 0 <= matrix[i][j] <= 2^31 - 1

代码1：DFS

package mainimport "fmt"func longestIncreasingPath(matrix [][]int) int {if len(matrix) == 0 || len(matrix[0]) == 0 {return 0}m, n := len(matrix), len(matrix[0])cache := make([][]int, m)for i := range cache {cache[i] = make([]int, n)}var dfs func(i, j int) intdfs = func(i, j int) int {if cache[i][j] != 0 {return cache[i][j]}dir := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}maxLen := 1for _, d := range dir {x, y := i+d[0], j+d[1]if x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[i][j] {length := 1 + dfs(x, y)if length > maxLen {maxLen = length}}}cache[i][j] = maxLenreturn maxLen}result := 0for i := 0; i < m; i++ {for j := 0; j < n; j++ {length := dfs(i, j)if length > result {result = length}}}return result
}func main() {matrix := [][]int{{9, 9, 4}, {6, 6, 8}, {2, 1, 1}}fmt.Println(longestIncreasingPath(matrix))matrix = [][]int{{3, 4, 5}, {3, 2, 6}, {2, 2, 1}}fmt.Println(longestIncreasingPath(matrix))matrix = [][]int{{1}}fmt.Println(longestIncreasingPath(matrix))
}

代码2：队列+拓扑排序

package mainimport "fmt"func longestIncreasingPath(matrix [][]int) int {if len(matrix) == 0 || len(matrix[0]) == 0 {return 0}m, n := len(matrix), len(matrix[0])inDegrees := make([][]int, m)for i := range inDegrees {inDegrees[i] = make([]int, n)}dir := [][]int{{-1, 0}, {1, 0}, {0, -1}, {0, 1}}queue := make([][2]int, 0)for i := 0; i < m; i++ {for j := 0; j < n; j++ {for _, d := range dir {x, y := i+d[0], j+d[1]if x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] < matrix[i][j] {inDegrees[i][j]++}}if inDegrees[i][j] == 0 {queue = append(queue, [2]int{i, j})}}}result := 0for len(queue) > 0 {result++size := len(queue)for i := 0; i < size; i++ {cur := queue[i]for _, d := range dir {x, y := cur[0]+d[0], cur[1]+d[1]if x >= 0 && x < m && y >= 0 && y < n && matrix[x][y] > matrix[cur[0]][cur[1]] {inDegrees[x][y]--if inDegrees[x][y] == 0 {queue = append(queue, [2]int{x, y})}}}}queue = queue[size:]}return result
}func main() {matrix := [][]int{{9, 9, 4}, {6, 6, 8}, {2, 1, 1}}fmt.Println(longestIncreasingPath(matrix))matrix = [][]int{{3, 4, 5}, {3, 2, 6}, {2, 2, 1}}fmt.Println(longestIncreasingPath(matrix))matrix = [][]int{{1}}fmt.Println(longestIncreasingPath(matrix))
}

输出：

4
4
1

---

330. 按要求补齐数组 Patching Array

给定一个已排序的正整数数组 nums ，和一个正整数 n 。从 [1, n] 区间内选取任意个数字补充到 nums 中，使得 [1, n] 区间内的任何数字都可以用 nums 中某几个数字的和来表示。

请返回 满足上述要求的最少需要补充的数字个数 。

示例 1:

输入: nums = [1,3], n = 6
输出: 1 
解释:
根据 nums 里现有的组合 [1], [3], [1,3]，可以得出 1, 3, 4。
现在如果我们将 2 添加到 nums 中， 组合变为: [1], [2], [3], [1,3], [2,3], [1,2,3]。
其和可以表示数字 1, 2, 3, 4, 5, 6，能够覆盖 [1, 6] 区间里所有的数。
所以我们最少需要添加一个数字。

示例 2:

输入: nums = [1,5,10], n = 20
输出: 2
解释: 我们需要添加 [2,4]。

示例 3:

输入: nums = [1,2,2], n = 5
输出: 0

提示：

• 1 <= nums.length <= 1000
• 1 <= nums[i] <= 10^4
• nums 按 升序排列
• 1 <= n <= 2^31 - 1

代码1：动态规划

package mainimport "fmt"func minPatches(nums []int, n int) int {dp := make([]bool, n+1)dp[0] = truefor _, num := range nums {for i := n; i >= num; i-- {if dp[i-num] {dp[i] = true}}}count := 0for i := 1; i <= n; i++ {if !dp[i] {count++for j := n; j >= i; j-- {if dp[j-i] {dp[j] = true}}}}return count
}func main() {nums1 := []int{1, 3}n1 := 6fmt.Println(minPatches(nums1, n1))nums2 := []int{1, 5, 10}n2 := 20fmt.Println(minPatches(nums2, n2))nums3 := []int{1, 2, 2}n3 := 5fmt.Println(minPatches(nums3, n3))
}

代码2：贪心算法 

package mainimport "fmt"func minPatches(nums []int, n int) int {count := 0      // 记录需要补充的数字个数index := 0      // 记录当前nums可表示的最大范围miss := 1       // 记录当前缺失的最小数字for miss <= n {if index < len(nums) && nums[index] <= miss {miss += nums[index] // 扩展当前范围index++} else {miss += miss // 补充缺失的数字count++}}return count
}func main() {nums1 := []int{1, 3}n1 := 6fmt.Println(minPatches(nums1, n1))nums2 := []int{1, 5, 10}n2 := 20fmt.Println(minPatches(nums2, n2))nums3 := []int{1, 2, 2}n3 := 5fmt.Println(minPatches(nums3, n3))
}

输出：

1
2
0

---

🌟 每日一练刷题专栏 🌟

✨ 持续，努力奋斗做强刷题搬运工！

👍 点赞，你的认可是我坚持的动力！ 

🌟 收藏，你的青睐是我努力的方向！ 

✎ 评论，你的意见是我进步的财富！  

☸ 主页：https://hannyang.blog.csdn.net/ 

	Rust每日一练 专栏 （2023.5.16~）更新中...
	Golang每日一练 专栏 （2023.3.11~）更新中...
	Python每日一练 专栏 （2023.2.18~2023.5.18）暂停更
	C/C++每日一练 专栏 （2023.2.18~2023.5.18）暂停更
	Java每日一练 专栏 （2023.3.11~2023.5.18）暂停更