所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

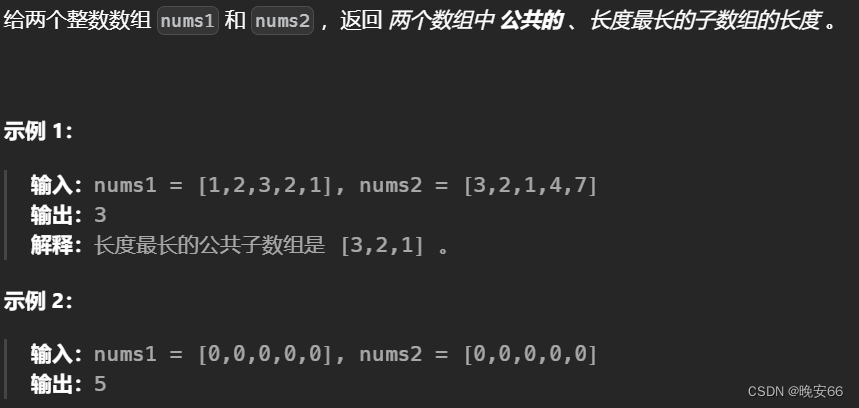
一、718、最长重复子数组

  思路分析：

• 第一步，动态数组的含义。$dp[i][j]$代表以下标$i-1$为结尾的nums1，和以下标$j-1$为结尾的nums2，最长重复子数组长度为$dp[i][j]$。
• 第二步，递推公式。根据$dp[i][j]$的定义，$dp[i][j]$的状态只能由$dp[i-1][j-1]$推导出来。

	if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;

• 第三步，元素初始化。dp数组中的所有元素都初始化为0。
• 第四步，递归顺序。一共有两层循环，先遍历nums1或者先遍历nums2都可以。
• 第五步，打印结果。题目要求长度最长的子数组的长度。所以在遍历的时候顺便把$dp[i][j]$的最大值记录下来。
    程序如下：

// 718、最长重复子数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;if (dp[i][j] > result) result = dp[i][j];}}return result;}
};

复杂度分析：

• 时间复杂度： $O(n\ast m)$，$n$和$m$分别是两个数组的长度。
• 空间复杂度：$O(n\ast m)$。

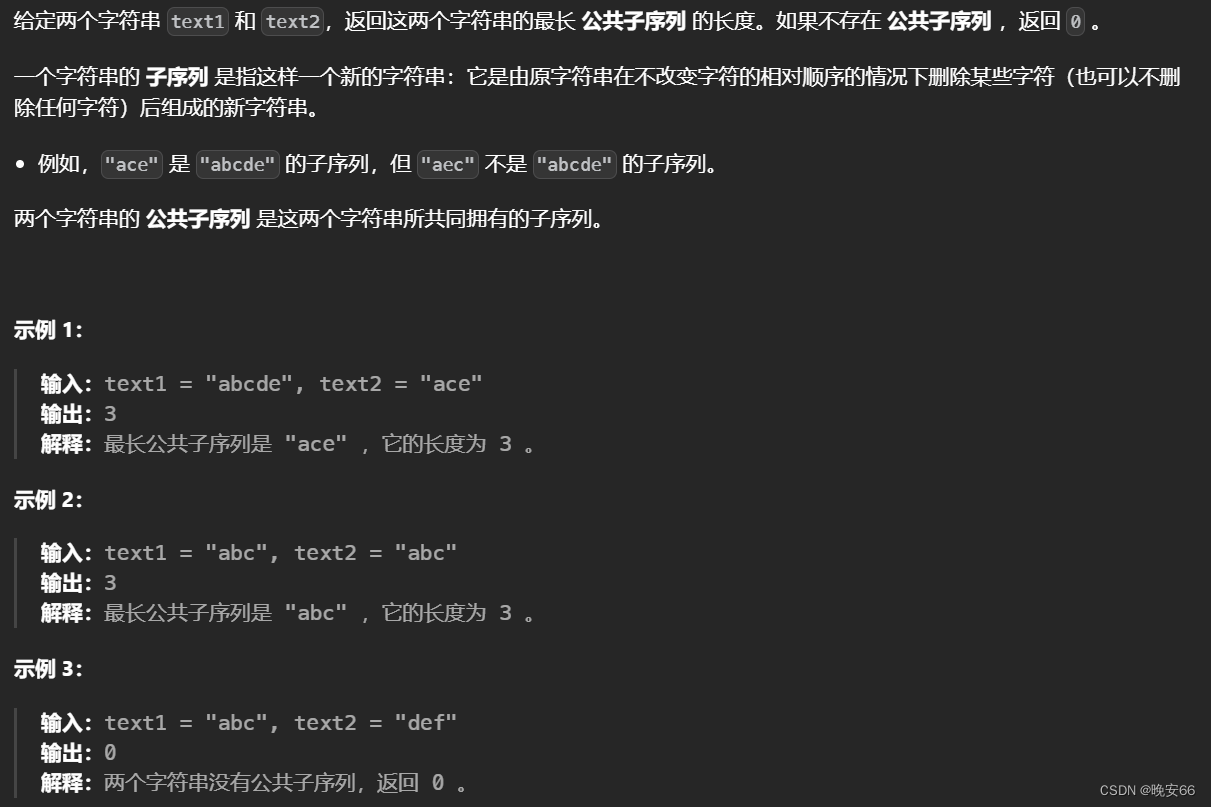
二、1143、最长公共子序列

  思路分析：

1. 第一步，动态数组的含义。$dp[i][j]$代表以下标$i-1$为结尾的text1，和以下标$j-1$为结尾的text2，最长公共子序列长度为$dp[i][j]$。
2. 第二步，递推公式。$dp[i][j]$可以由两种情况推导出来：

• $text1[i-1]$与 $text2[j-1]$相同：那么找到一个公共元素，$dp[i][j]=dp[i-1][j-1]+1$。
• $text1[i-1]$ 与 $text2[j-1]$不相同：那么$text1[0,i-2]$与$text2[0,j-1]$的最长公共子序列 和 $text1[0,i-1]$与$text2[0,j-2]$的最长公共子序列，取最大的。

	if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);

• 第三步，元素初始化。dp数组中的所有元素都初始化为0。
• 第四步，递归顺序。一共有两层循环，从前往后进行遍历。
• 第五步，打印结果。题目要求最长公共子序列的长度。所以在遍历的时候顺便把$dp[i][j]$的最大值记录下来。
    程序如下：

// 1143、最长公共子序列
class Solution2 {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));int result = 0;for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if(dp[i][j] > result) result = dp[i][j];}}return result;}
};

复杂度分析：

• 时间复杂度： $O(n\ast m)$，$n$和$m$分别是两个序列的长度。
• 空间复杂度：$O(n\ast m)$。

三、完整代码

# include <iostream>
# include <vector>
# include <string>
using namespace std;// 718、最长重复子数组
class Solution {
public:int findLength(vector<int>& nums1, vector<int>& nums2) {vector<vector<int>> dp(nums1.size() + 1, vector<int>(nums2.size() + 1, 0));int result = 0;for (int i = 1; i <= nums1.size(); i++) {for (int j = 1; j <= nums2.size(); j++) {if (nums1[i - 1] == nums2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;if (dp[i][j] > result) result = dp[i][j];}}return result;}
};// 1143、最长公共子序列
class Solution2 {
public:int longestCommonSubsequence(string text1, string text2) {vector<vector<int>> dp(text1.size() + 1, vector<int>(text2.size() + 1, 0));int result = 0;for (int i = 1; i <= text1.size(); i++) {for (int j = 1; j <= text2.size(); j++) {if (text1[i - 1] == text2[j - 1]) dp[i][j] = dp[i - 1][j - 1] + 1;else dp[i][j] = max(dp[i - 1][j], dp[i][j - 1]);if(dp[i][j] > result) result = dp[i][j];}}return result;}
};int main() {//vector<int> nums1 = { 1, 2, 3, 2, 1 }, nums2 = { 3, 2, 1, 4, 7 };//Solution s1;//int result = s1.findLength(nums1, nums2);string text1 = "abcde", text2 = "ace";Solution2 s1;int result = s1.longestCommonSubsequence(text1, text2);cout << result << endl;system("pause");return 0;
}

end