【学习笔记】详解换根法(换根DP)-编程知识

一.换根DP的概念

1.换根DP是什么？

换根DP，又叫二次扫描，是树形DP的一种。

2.换根DP能解决什么问题？

换根DP能解决不指定根结点，并且根节点的变化会对一些值产生影响的问题。例如子结点深度和、点权和等。如果要 暴力求解出最优解，则我们可以枚举所有的节点为根，然后分别跑一次搜索，这样的时间复杂度会达到 O( $n^{2}$ )，显然不可接受。这时可以考虑使用换根DP解决。

3.换根DP与一般的树形DP相比有什么不同?

其相比于一般的树形DP具有以下特点：

以树上的不同点作为根，其解不同。
为其求解答案，不能单求某点的信息，需要求解每个节点的信息。
无法通过一次搜索完成答案的求解，因为一次搜索只能得到一个节点的答案。

二.换根DP的解法

换根dp通常会与树形dp 结合，我们可以先任定一个根节点root，通过树形dp的思想计算出一个答案。但这样求解出的答案只是以root为根的解，并不能确定是不是最优解。于是再考虑当root的子节点作为根节点时，答案怎样变化。一般可以在 O(1) 的时间复杂度内完成答案的转化。这样整道题的时间复杂度就由 O( $n^{2}$ ) 降为了 O(n)。

总结一下,换根DP总共是三个步骤:

指定某个节点为根节点。
第一次搜索完成预处理（如子树大小等），同时得到以上述节点为根的解。
第二次搜索进行换根的动态规划，由已知解的节点推出相连节点的解。

如果到了这里还没有听懂的话,不用慌,可以结合下面的例题慢慢理解。

三.例题精讲

1.STA-Station

question

sol

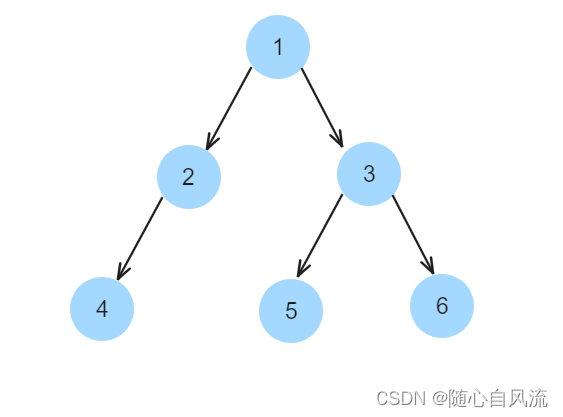
我们先来画一下样例~(这里先假设以1号节点为根)

在这幅图中,siz[i]表示以i节点为根的子树中节点个数(包括i节点本身)，而deep[i]表示i在以1号节点为根时的深度(1号节点深度为1)。

注意:代码中其实不需要开deep数组(第一次dfs时可以直接在dfs设置一个变量dep，然后每次递归时直接将以一号节点为根的解加上dep就行了)，但是为了方便解释，我还是画上了。

这样，我们就可以得出来以1为根时深度之和(也就是解)为1+2+3+3+3+4+5+5=26。

然后我们就可以进行换根操作(比如此时以1的子节点4号节点为根)

siz我们依然沿用第一次得到的结果,deep我为了方便演示已经更新了。

从中我们可以发现一些规律。这棵树中从前(以1号节点为根时)属于4的子树的节点(2，3，4，5，6，7，8)的深度都减了1，而其他的节点(这里样例中只有1)的深度都加了1。大家可以自行在纸上多画几个换根后的图，加深理解。

归纳一下我们得到的结论:

如果此时要将根节点换成节点x

那么，以x为根时的解就是:

以x的父节点为根的子树的节点数-以x为根的子树的节点数+(总节点数-以点为根的子树的节点数)

↑ ↑ ↑

以x为根时的解的基数这些节点的深度都要-1(在这里省略了乘1) 其他的节点的深度都要+1

假设dh[x]代表以x为根时的解，fa为x的父节点

则dh[x] = dh[fa] - siz[x] + (n - siz[x])

总结一下:

我们假设此时将根节点换成节点x，则其子树由两部分构成，第一部分是其原子树，第二部分则是1号节点的其他子树。
根从1号节点变为节点x的过程中，我们可以发现第一部分的深度降低了1，第二部分的深度则上升了1，而这两部分节点的数量在第一次搜索时就得到了(siz数组)。
DP公式:dh[x] = dh[fa] - siz[x] + (n - siz[x])

最后还要注意:第二次dfs后我们还要枚举dh[1~n]取其中的最大值才能得到答案！

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
vector<int> vec[2000001];
int n,u,v,siz[2000001],dh[2000001],ans;
void dfs(int x,int fa,int dep)
{siz[x] = 1;//因为以x节点为根的子树包括x自身dh[1] += dep;//求以1节点为根的解for(int i = 0; i < vec[x].size(); i++){int son = vec[x][i];if(son != fa){dfs(son,x,dep + 1);siz[x] += siz[son];//不断累加子树中的节点个数}}
}
void dfs_2(int x,int fa)
{if(x != 1) dh[x] = dh[fa] - siz[x] + (n - siz[x]);//DP公式for(int i = 0; i < vec[x].size(); i++){int son = vec[x][i];if(son != fa) dfs_2(son,x);}
}
signed main()
{cin>>n;for(int i = 1; i < n; i++){cin>>u>>v;vec[u].push_back(v);//建树vec[v].push_back(u);}dfs(1,0,1);dfs_2(1,0);for(int i = 1; i <= n; i++) ans = max(ans,dh[i]);//取以各个节点为根的解的最大值cout<<ans;return 0;
}

2.[USACO10MAR] Great Cow Gathering G

question

sol

这道题与例题基本是一致的，只是添加了每个节点和每条边的权值，在DP时注意加上与乘上即可，没有什么大的变形。如果实在不会，可以结合下面的代码理解。

code

#include <bits/stdc++.h>
#define int long long
using namespace std;
struct ff
{int len,id;
};
vector<ff> vec[100001];
int n,u,v,siz[1000001],dh[1000001],ans,w,c[1000001],s;
void dfs(int x,int fa)
{siz[x] = c[x];//以x为根的1子树是包括x节点本身的,所以siz[x]要初始化成x节点上的奶牛个数for(int i = 0; i < vec[x].size(); i++){int son = vec[x][i].id;if(son != fa){dfs(son,x);siz[x] += siz[son];//不断累加以子节点为根的子树上的奶牛数dh[1] += siz[son] * vec[x][i].len;//因为题目中添加了边权和点权,故不能像sta那题一样直接+dep}}
}
void dfs_2(int x,int fa)
{for(int i = 0; i < vec[x].size(); i++){int son = vec[x][i].id;if(son != fa){dh[son] = dh[x] - siz[son] * vec[x][i].len + (s - siz[son]) * vec[x][i].len;//此处可以自行画图推导一下dfs_2(son,x);}}
}
signed main()
{cin>>n;for(int i = 1; i <= n; i++){cin>>c[i];s += c[i];//s:奶牛的总数}for(int i = 1; i < n; i++){cin>>u>>v>>w;vec[u].push_back({w,v});//邻接表建双向边vec[v].push_back({w,u});}dfs(1,0);dfs_2(1,0);ans = 1e18;for(int i = 1; i <= n; i++) ans = min(ans,dh[i]);//因为要求深度最小,所以是取解的最小值cout<<ans;return 0;
}