1、257. 二叉树的所有路径
要求返回根节点到叶子节点的所有路径,这里用前序遍历就好。
每次递归前,都让字符串s加上当前节点的值和“->”,然后判断是否为叶子节点,如果是的话,说明这条路径是一个答案,因为最后多一个->,所以用substring去掉。
如果root是null,那么root.left和root.right可能会空指针异常。所以每次递归的时候都要做一下判断。
class Solution {List<String> list = new ArrayList<>();public List<String> binaryTreePaths(TreeNode root) {String s = "";pre(root, s);return list;}public void pre(TreeNode root, String s){s += root.val+"->";if(root.left == null && root.right == null){list.add(s.substring(0, s.length()-2));return;}if(root != null && root.left != null) pre(root.left, s);if(root != null && root.right != null) pre(root.right, s);}}2、110. 平衡二叉树
我用的比较好想的方法,直接用非递归的方式前序遍历每个节点,在出栈的时候进行检查,检查每个节点的左右孩子最大高度差是否符合要求。
class Solution {public boolean isBalanced(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();while(root != null || !stack.isEmpty()){if(root != null){stack.push(root);root = root.left;}else{//检查TreeNode t = stack.pop();if(Math.abs(H(t.left) - H(t.right)) > 1){return false;}root = t.right;}}return true;}public int H(TreeNode root){if(root == null) return 0;return Math.max(H(root.left), H(root.right))+1;}
}3、222. 完全二叉树的节点个数
直接遍历即可。
class Solution {public int countNodes(TreeNode root) {LinkedList<TreeNode> stack = new LinkedList<>();int cnt = 0;while(root != null || !stack.isEmpty()){if(root != null){cnt++;stack.push(root);root = root.left;}else{TreeNode t = stack.pop();root = t.right;}}return cnt;}
}4、105. 从前序与中序遍历序列构造二叉树
前序:1 2 4 3 6 7
中序:4 2 1 6 3 7
首先,要确认根节点的值,根节点就是前序遍历的第一个节点。
于是我们得到根:1
然后在中序的数组中找到根,因为中序是 左根右 的顺序,所以根的左右两侧就是左子树
左:4 2
右:6 3 7
同样的,我们遍历左子树4 2,在前序中找到根,得到根是2,于是开始循环······
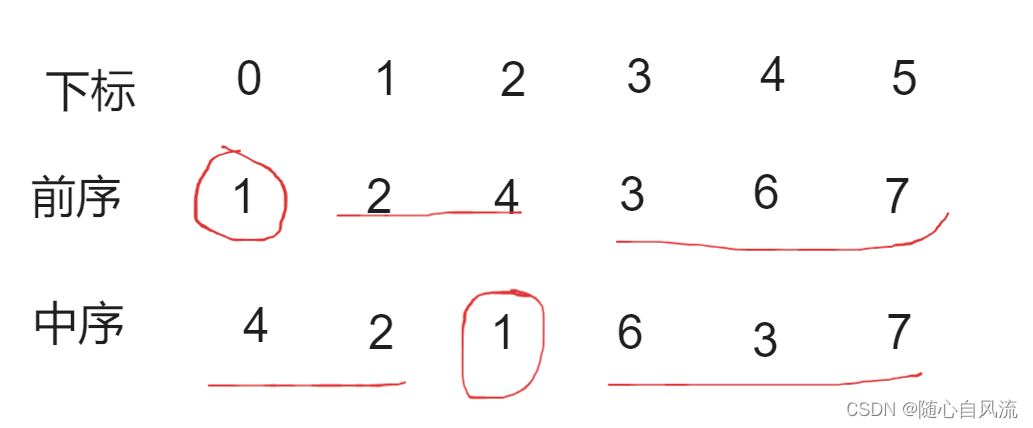
观察以上内容,我们可以这样做:找到前序遍历的节点,然后循环遍历中序数组,找到第i个元素是根节点,这时候继续递归寻找左子树,左子树的前序数组下标为1~i,中序数组为0~i-1;右子树的前序数组下标为i+1~len-1,中序数组为i+1~len-1
因为两个数组长度相同,所以判断退出条件写一个即可。
当然这样效率比较低,但是确实比较好理解一些。
class Solution {public TreeNode buildTree(int[] preorder, int[] inorder) {return buildByPreAndIn(preorder, inorder);}public TreeNode buildByPreAndIn(int[] pre, int[] in){if(pre.length == 0) return null;//根节点TreeNode root = new TreeNode(pre[0]);for(int i = 0; i < in.length; i++){if(root.val == in[i]){//区分左右子树 in是 0~i-1 i+1 ~ len-1 pre是1 ~ i i+1 ~ len-1root.left = buildByPreAndIn(Arrays.copyOfRange(pre, 1, i+1), Arrays.copyOfRange(in, 0, i));root.right = buildByPreAndIn(Arrays.copyOfRange(pre, i+1, in.length), Arrays.copyOfRange(in, i+1, in.length));break;}}//每次返回根节点return root;}
}class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}5、106. 从中序与后序遍历序列构造二叉树
跟上一个题区别不大,后序最后一个数就是根节点,也是从中序数组中找到根,然后又分成左右子树······
我们可以根据前序中序,也可以根据中序后序建树,但是不可以根据前序后序建树,因为前面两个方式,我们都可以通过前序或者后序明确得到根节点,然后根据中序划分左右子树,但是如果只有前序和后序,我们得到根节点之后,无法确定如何划分左右子树。
class Solution {public TreeNode buildTree(int[] inorder, int[] postorder) {return buildByInAndPost(inorder, postorder);}public TreeNode buildByInAndPost(int[] in, int[] post){if(in.length == 0) return null;TreeNode root = new TreeNode(post[post.length - 1]);for(int i = 0; i < in.length; i++){if(in[i] == root.val){root.left = buildByInAndPost(Arrays.copyOfRange(in, 0, i), Arrays.copyOfRange(post, 0, i));root.right = buildByInAndPost(Arrays.copyOfRange(in, i+1, in.length), Arrays.copyOfRange(post, i, post.length-1));break;}}return root;}
}
public class TreeNode {public int val;public TreeNode left;public TreeNode right;public TreeNode(int val) {this.val = val;}public TreeNode(int val, TreeNode left, TreeNode right) {this.val = val;this.left = left;this.right = right;}
}