1、什么是BCD码?
BCD码是一种2进制的数字编码形式,用4位2进制数来表示1位10进制中的0~9这10个数。这种编码技术,最常用于会计系统的设计里,因为会计制度经常需要对很长的数字做准确的计算。相对于一般的浮点式记数法,采用BCD码,既可保存数值的精确度,又可使电脑免除作浮点运算所耗费的时间。此外,对于其他需要高精确度的计算,BCD编码也很常用。
常见的BCD码有很多种形式,比如8421码、2421码、5421码、余3码等等,其中最常用的是8421码,接下来的讨论都建立在8421BCD码的基础上。
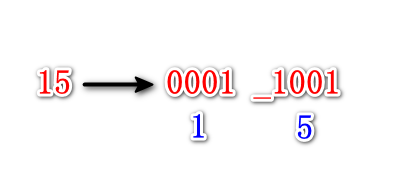
BCD码的一个很大的优势是可以很方便的用2进制来显示10进制数。比如10进制数15如果用2进制存储,就是1111,也就是16进制的F,如果它显示在数码管上是“F”,但是这种显示方式对我们来说其实并不友好,我们更习惯地还是“1 5”。

而BCD码存储10进制数15,则需要8位,高4位存储十位“1”,低四位存储个位“5”,也就是“0001”和“1001”,这样就可以做到把“1”和“5”这两个数字分别显示了:
BCD码的一般形式如下:
| 十进制数 | BCD码 |
|---|---|
| 0 | 0 0 0 0 |
| 1 | 0 0 0 1 |
| 2 | 0 0 1 0 |
| 3 | 0 0 1 1 |
| 4 | 0 1 0 0 |
| 5 | 0 1 0 1 |
| 6 | 0 1 1 0 |
| 7 | 0 1 1 1 |
| 8 | 1 0 0 0 |
| 9 | 1 0 0 1 |
2、2进制码转BCD码
如何将2进制码转换为BCD码?4位的转换相对简单,只要根据数值的大小加6就可以了。因为4位二进制码可以表示0-15这16个数,而BCD码只能表示0-9这10个数。也就是说4位2进制数逢16进位,而4位BCD逢10进位,所以需要加6这个差值来给它人工进位。比如4位2进制数1111(10进制15),加上6后,为1111+1010 = 1_1001,高位可以视作补齐3个0,即0001_1001,0001表示1,1001表示5。
2.1、除法和取模
加6修正法只适用于4位的转换,位数高了以后,这个方法就不适用了。比如1_1111(F)加上6后,显然就没用。
多位数的2进制码转BCD码有一种很容易想到的办法:利用除法和取模。比如8位2进制数可以表示的范围是0~255,那么就可以用3个4bit数来分别表示个位、十位和百位。以255为例:
个位 = 255%10 = 5;
十位 = 255% 100 / 10 = 55/10 = 5;
百位 = 255/100 = 2;
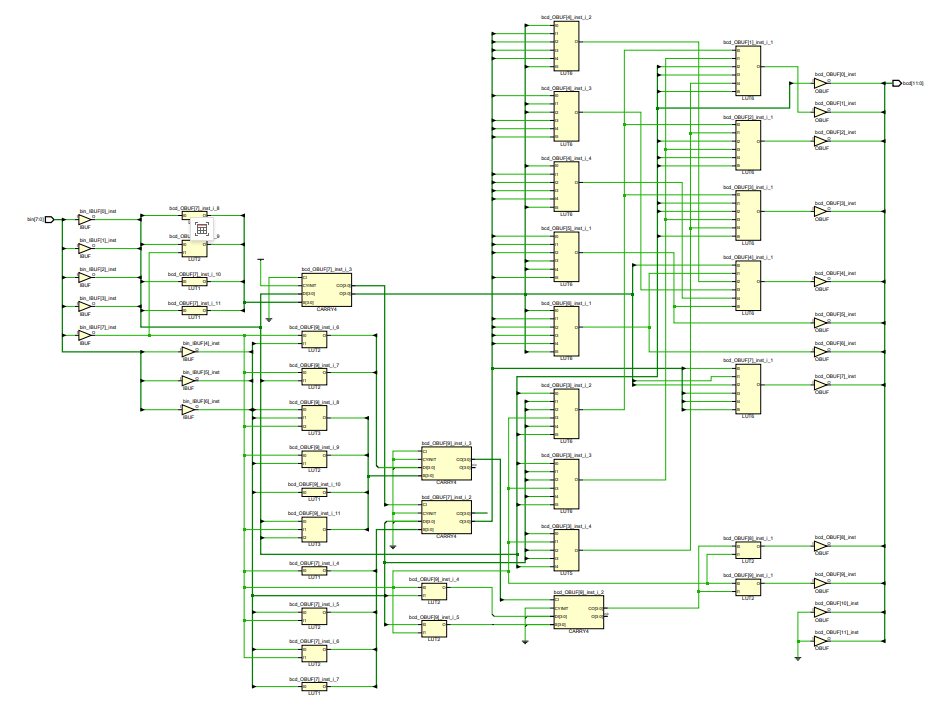
这种方法在逻辑上理解起来非常简单,但是有个很大的缺点就是涉及到了除法和取模操作。众所周知,用FPGA做除法和取模操作将消耗大量的逻辑资源,而且时序也容易跑不高。下面是这种方法的RTL:
`timescale 1 ns/1 ns
module test(input [7 :0] bin,output [11:0] bcd
);wire [3:0] ones,tens,huns; assign ones = bin % 10;
assign tens = bin % 100 / 10;
assign huns = bin / 100;
assign bcd = {huns,tens,ones};endmodule
这样综合出来的电路确实面积不小,一共用了27个LUT,逻辑级数5级:
编写Testbench对电路进行测试:
`timescale 1 ns/1 ns
module tb_test;reg [7:0] bin;
wire [11:0] bcd;integer i,j;
reg [8:0] err; //错误计数器
reg [11:0] bcd_true[0:255]; //进行对比的正确输出//例化被测试模块
test u_test (.bin (bin), .bcd (bcd)
);//生成做对比的正确输出
initial beginfor(j=0;j<256;j=j+1)beginbcd_true[j][3 :0] = j % 10;bcd_true[j][7 :4] = j % 100 / 10;bcd_true[j][11:8] = j / 100;end
end//生成测试激励
initial beginerr = 0;for(i=0;i<256;i=i+1)beginbin = i; #10; if(bcd_true[bin] != bcd )begin //如果转换有误$display("%3d is Wrong!",bin); //打印错误输入err = err + 1; //统计错误个数end end $display("Test Complete!%3d errs!",err);//打印结束仿真信息,并输出错误个数$stop; //结束仿真
endendmodule
这个TB文件添加了自动对比机制,所以我们只需要关注窗口打印的信息:

稍微看下波形也可以知道,仿真结果是没问题的(bin是10进制显示,bcd是16进制显示):

2.2、查找表法
位数不多的情况下还有一种更简单的方法–查找表法。查找表法的原理很简单,把所有输入所对应的输出都放到一个ROM里边存起来,然后通过地址寻址方式来取值就行了。比如5位2进制数的转换则只需要储存0~31这32个数值就行,8位2进制数也只需要存储256个数值。
下面是用查找表法写的8位2进制数转BCD的代码,需要注意的是,由于篇幅过长,省去了部分代码,而且为了有对比,故意把最后两个数即8‘d254和8‘d255的输出弄成了错误输出。
module test(input [7:0] bin,output reg [11:0] bcd
);always @(*)begincase(bin)8'd 0:bcd=12'b000000000000;8'd 1:bcd=12'b000000000001;8'd 2:bcd=12'b000000000010;//这里开始省略了很多次赋值8'd254:bcd=12'b001001010000; //这里是故意弄错了8'd255:bcd=12'b001001010001; //这里是故意弄错了 default:bcd=12'b000000000000;endcase
end endmodule
除了采用case语句赋值的方式外,还有很多其他实现查找表的方式,比如例化ROM,或者用综合属性执行生成DRAM等。这样综合出来的电路结构用了13个LUT+4个MUX,比起之前的方法(27个LUT)少用了很多资源。
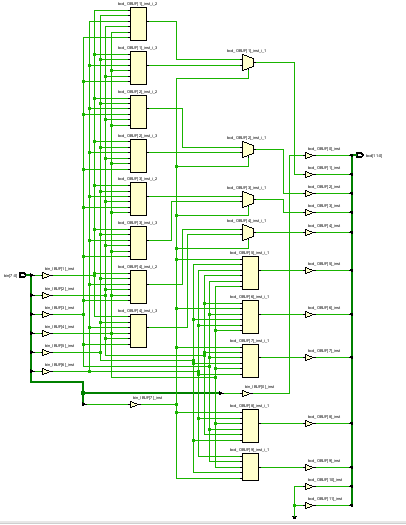
仿真用同样的TB就行,这是仿真结果:

因为之前故意把8‘d254和8‘d255这两个数弄错了,所以这里检测到了并打印了出来,其他仿真结果无误。
2.3、Double dabble(移位加3法)
4位二进制大于15才进位,而BCD码是大于9就进位,若4位二进制大于9时进位,这样得到的就是15的BCD码,因此将大于9的四位二进制数加6就能得到其BCD码。对于大于四位的二进制数,通过左移,逢9加6进位,即可转换任意位的二进制数,比如说,对于5位二进制数,由高4位二进制数左移一位得到,那么将前4位得到的BCD码也左移一位,并重新判断低四位是否大于4,若大于4,则加3进位,即可得到5位二进制数对应的BCD码。这种算法叫Double dabble,中文叫移位加3法。
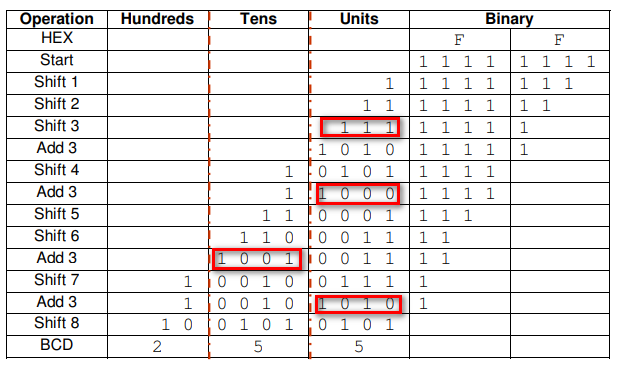
上图展示了这种方法的详细过程,二进制数1111_1111(10进制数255)从高位开始依次向左移位,移入到3个4bit组成的12位寄存器了,然后判断每个4bit是否大于4,若是则+3修正,然后继续移位。判断大于4是因为左移相当于乘以2,实际上就是在判断是否大于10产生了进位,而+3经过左移后会变成+6,同样是对2进制与BCD不同位进位所进行的修正。
所以这一过程是:从高位开始移位>>判断每个4bit是否大于4,若是则加3>>重复操作,直到所有位都被移出。
下面以8位2进制数转BCD为例,它的过程应该是这样的:

在这个电路中,Adder模块实现输入大于4就加3进位的功能
0和高3位构成左移3次后的低四位,经过Adder1模块后,得到调整后的数据
其他位类推
最后,在高位填0并与最低位的a0构成最终左移八次的十二位数据
首先设计大于4就加3模块:
//如果大于4就+3
module add3_g4(input [3 : 0] in,output reg [3 : 0] out
);//利用查找表实现+3操作
always @ (*) begincase (in) 4'b0000 : out = 4'b0000;4'b0001 : out = 4'b0001;4'b0010 : out = 4'b0010;4'b0011 : out = 4'b0011;4'b0100 : out = 4'b0100;4'b0101 : out = 4'b1000;4'b0110 : out = 4'b1001;4'b0111 : out = 4'b1010;4'b1000 : out = 4'b1011;4'b1001 : out = 4'b1100;default : out = 4'b0000;endcase
end
endmodule
然后是主模块(其实就是模块化设计方法,简称连连看)
module test(input [7:0] bin,output [11:0] bcd
);wire [3 : 0] t1, t2, t3, t4, t5, t6, t7;add3_g4 adder1(.in ({1'b0, bin[7 : 5]}),.out(t1[3 : 0])
);
add3_g4 adder2(.in ({t1[2 : 0], bin[4]}),.out(t2[3 : 0])
);
add3_g4 adder3(.in({t2[2 : 0], bin[3]}),.out(t3[3 : 0])
);
add3_g4 adder4(.in({1'b0, t1[3], t2[3], t3[3]}),.out(t4[3 : 0])
);
add3_g4 adder5(.in({t3[2 : 0], bin[2]}),.out(t5[3 : 0])
);
add3_g4 adder6(.in({t4[2 : 0], t5[3]}),.out(t6[3 : 0])
);
add3_g4 adder7(.in({t5[2 : 0], bin[1]}),.out(t7[3 : 0])
);assign bcd = {2'b0, t4[3], t6[3 : 0], t7[3 : 0], bin[0]};endmodule
这种方法综合出来只用了10个LUT,资源消耗甚至比查找表法还少。
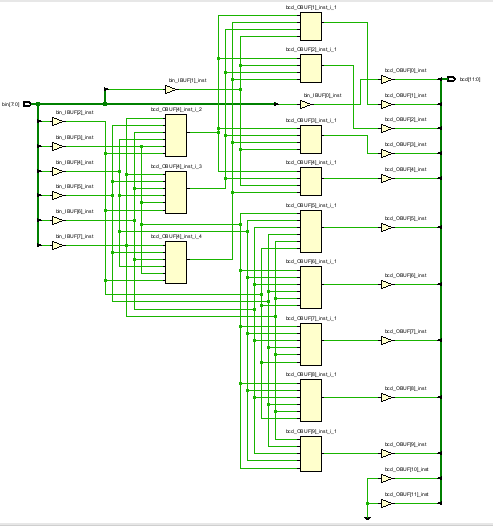
再用同样的TB仿真,仿真结果表明这个设计没问题:
这种模块化的设计方法有2个很不好的地方
- 不够抽象,需要把图画出来才能理解
- 几乎没有可拓展性,如果改变位数则RTL需要大改
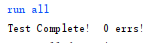
所以接下来,设计一个位宽可变的、抽象程度更高的电路:
module test
#( parameter W = 8 //输入位宽可变
)
( input [W-1 :0] bin, output reg [W+(W-4)/3:0] bcd
); integer i,j; //循环参数always @(*) beginfor(i = 0; i <= W+(W-4)/3; i = i+1) bcd[i] = 0; //用全0初始化bcd[W-1:0] = bin; //低位用输入替换for(i = 0; i <= W-4; i = i+1) for(j = 0; j <= i/3; j = j+1) if (bcd[W-i+4*j -: 4] > 4) //如果大于4bcd[W-i+4*j -: 4] = bcd[W-i+4*j -: 4] + 4'd3; //+3
endendmodule
这样综合出来的电路面积也很小,只用了11个LUT:

使用这个模块的时候需要注意的一点是,它的输出参数化设计是设计得最小的模块。比如8位2进制数最大为255,实际上用10个bit的BCD码就可以表示,但是我们一般习惯用12个bit来表示,所以可以在最后的结果前面补0。
2.4、使用资源对比
将输入位数扩大到16位2进制数的转换,再分别使用3个方法构建电路,观察资源消耗情况:
| 除法和取模 | 查找表 | 移位加3 |
|---|---|---|
| 287个LUT | 23220个LUT或者36个BRAM | 71个LUT |
可以看到随着输入位数的增加,移位加3法的优势就更明显。一般来讲。查找表法适合位数不多的情况;而直接用除法则非常省事,适合对资源消耗和时序都没什么要求的时候使用。
3、BCD码转2进制码
了解了如何从2进制码转BCD码后,那么从BCD码转2进制码的方法就简单了–无非就是上述方法的逆过程嘛!
3.1、查找表
这个没什么好说的,和2进制码转BCD码的流程一模一样,只是ROM里面的存储内容不同罢了。
3.2、乘法(直接乘法与移位加法)
以12位BCD码255为例,若转换成2进制码,则只需要8bit。最高位的2可以看做百位,中间的5可以看做十位,最低位的5可以看做个位,所以转换后应该是2*100+5*10+5=255(10进制)=1111_1111(2进制)。只用乘法就可以实现BCD码转2进制码,由于乘法可以转换成移位和加法,所以消耗的资源也不会特别多。
下面是直接用乘法来实现20位BCD转16位BIN的RTL:
//乘法:20位BCD转16位BIN,加上时钟,49lut+24carry4
//slak=2.381ns,观察FMAX = 131Mhz,逻辑级数8
module test(input clk,input [19:0] bcd,output reg [15:0] bin
);wire [3:0] ten_thos; //10000
wire [3:0] thos; //1000
wire [3:0] huns; //100
wire [3:0] tens; //10
wire [3:0] ones; //1wire [19:0] ten_thos_shift;
wire [19:0] thos_shift;
wire [19:0] huns_shift;
wire [19:0] tens_shift; reg [19:0] bcd_r;always @(posedge clk) //输入寄存一拍bcd_r <= bcd;
always @(posedge clk) //输出寄存一拍 bin <= ten_thos_shift + thos_shift+ huns_shift + tens_shift + ones; assign ten_thos = bcd_r[19:16];
assign thos = bcd_r[15:12];
assign huns = bcd_r[11:8];
assign tens = bcd_r[7 :4];
assign ones = bcd_r[3 :0]; assign ten_thos_shift = ten_thos*10000;
assign thos_shift = thos*1000;
assign huns_shift = huns*100;
assign tens_shift = tens*10;endmodule
这样综合出来的电路一共消耗49个LUT+24个CARRY4,最大逻辑级数为8,Fmax约为131Mhz。

用移位和加法来实现乘法:
//移位加法实现乘法,加上时钟,53 lut+ 13 carry4
//slack5.517ns,观察FMAX = 223Mhz,逻辑级数7
module test(input clk,input [19:0] bcd,output reg [15:0] bin
);wire [3:0] ten_thos; //10000
wire [3:0] thos; //1000
wire [3:0] huns; //100
wire [3:0] tens; //10
wire [3:0] ones; //1wire [19:0] ten_thos_shift;
wire [19:0] thos_shift;
wire [19:0] huns_shift;
wire [19:0] tens_shift; reg [19:0] bcd_r;always @(posedge clk) //输入寄存一拍bcd_r <= bcd;
always @(posedge clk) //输出寄存一拍 bin <= ten_thos_shift + thos_shift+ huns_shift + tens_shift + ones; assign ten_thos = bcd_r[19:16];
assign thos = bcd_r[15:12];
assign huns = bcd_r[11:8];
assign tens = bcd_r[7 :4];
assign ones = bcd_r[3 :0]; //移位后的万位=1*10000=1*(8192+1024+512+256+16)
assign ten_thos_shift = (ten_thos<<13) + (ten_thos<<10) + (ten_thos<<9) + (ten_thos<<8) + (ten_thos<<4);
//移位后的千位=1*1000=1*(1024-16-8)
assign thos_shift = (thos<<10) - (thos<<4) - (thos<<3);
//移位后的百位=1*100=1*(64+32+4)
assign huns_shift = (huns<<6) + (huns<<5) + (huns<<2);
//移位后的十位=1*10=1*(8+2)
assign tens_shift = (tens<<3) + (tens<<1);endmodule
这样综合出来的电路一共消耗53个LUT+13个CARRY4,最大逻辑级数为7,Fmax为223Mhz,电路性能是比直接用乘法要好的。

3.3、移位减3法
移位加3法的逆过程自然就是移位减3发,但是注意判断条件–BCD码逢十进一,四位二进制逢十六进一,所以转二进制的条件即为16/2=8(右移),即需要判断每个BCD码的4位是否大于等于8,同时向右移位到二进制码中。
下面展示了BCD码0010_0100_0011到2进制码1111_0011的过程。
BCD Input Binary Output2 4 30010 0100 0011 00000000 初始化0001 0010 0001 10000000 向右移位0000 1001 0000 11000000 向右移位0000 0110 0000 11000000 中间4位值为9,所以要-30000 0011 0000 01100000 向右移位0000 0001 1000 00110000 向右移位0000 0001 0101 00110000 最右4位值为8,所以要-30000 0000 1010 10011000 向右移位0000 0000 0111 10011000 最右4位值为10,所以要-30000 0000 0011 11001100 向右移位0000 0000 0001 11100110 向右移位0000 0000 0000 11110011 向右移位
下面的RTL实现了12位BCD码转8位2进制码:
module test
( input [11:0] bcd, output reg [7 :0] bin
); integer i,j; //循环参数
reg [11:0] temp;always @(*) begintemp[11:0] = bcd; //用输入替换for(i = 1; i <= 7; i = i+1) begin for(j = 0; j <= (7-i)/4; j = j+1) begin if (temp[i+4*j +: 4]>=8)begin // if > 4temp[i+4*j +: 4] = temp[i+4*j +: 4] - 4'd3; //-3endend end bin= temp;
endendmodule
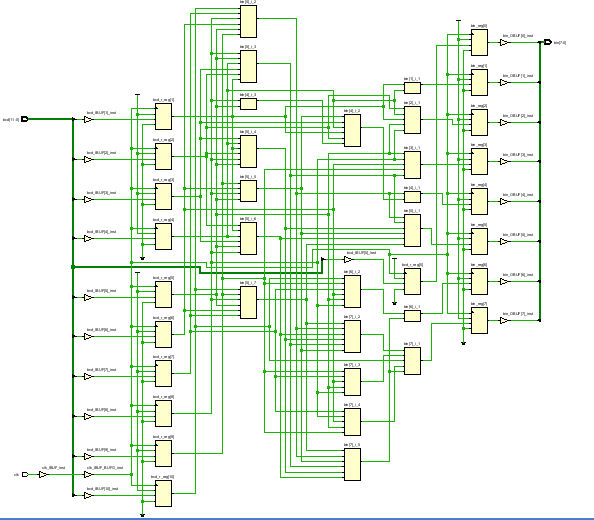
这样综合出来的电路一共消耗17个LUT,最大逻辑级数为3,Fmax为323Mhz。

下面是20位BCD转16位BIN的RTL:
module test
(input [19:0] bcd, output reg [15:0] bin
); integer i,j; //循环参数
reg [19:0] temp; always @(*) begintemp = bcd; //输入替换for(i = 1; i <= 15; i = i+1) begin //16-1 for(j = 0; j <= (15-i)/4; j = j+1) begin if (temp[i+4*j +: 4]>=8)begin // if > 4temp[i+4*j +: 4] = temp[i+4*j +: 4] - 4'd3; //+3endend end bin= temp;
endendmodule
3.4、资源及时序对比
将输入位数扩大到20位BCD转16位2进制数的转换,再分别使用3个方法构建电路,观察资源消耗情况:
| 直接乘 | 移位+加法 | 查找表 | 移位-3法 |
|---|---|---|---|
| 49个LUT+24个CARRY4 | 53 lut+ 13 carry4 | 23220个LUT或者36个BRAM | 71个LUT |
| FMAX = 131Mhz,逻辑级数8 | FMAX = 223Mhz,逻辑级数7 | / | FMAX = 147Mhz,逻辑级数7 |
移位减3法和直接乘法的资源消耗以及速度都差不多,这是因为乘法容易乘转换成移位+加法,这是FPGA很容易实现的形式,并不会像除法和取模那样消耗非常多的资源。用移位+加法来实现乘法的形式的资源消耗和时序性能是最好的,所以BCD转2进制数,建议用左移+加法来实现乘法。
4、总结
- 位数不多的情况下,BCD码与2进制码的互转用查找表法都是最好的实现形式
- 位数较多的情况下,2进制码转BCD码更推荐用移位加3法;BCD码转2进制码更推荐用移位+加法来实现乘法的形式
------------ | ---------------------- | ----------------------- |
| 49个LUT+24个CARRY4 | 53 lut+ 13 carry4 | 23220个LUT或者36个BRAM | 71个LUT |
| FMAX = 131Mhz,逻辑级数8 | FMAX = 223Mhz,逻辑级数7 | / | FMAX = 147Mhz,逻辑级数7 |
移位减3法和直接乘法的资源消耗以及速度都差不多,这是因为乘法容易乘转换成移位+加法,这是FPGA很容易实现的形式,并不会像除法和取模那样消耗非常多的资源。用移位+加法来实现乘法的形式的资源消耗和时序性能是最好的,所以BCD转2进制数,建议用左移+加法来实现乘法。
4、总结
- 位数不多的情况下,BCD码与2进制码的互转用查找表法都是最好的实现形式
- 位数较多的情况下,2进制码转BCD码更推荐用移位加3法;BCD码转2进制码更推荐用移位+加法来实现乘法的形式
- 📣您有任何问题,都可以在评论区和我交流📃!
- 📣本文由 孤独的单刀 原创,首发于CSDN平台🐵,博客主页:wuzhikai.blog.csdn.net
- 📣您的支持是我持续创作的最大动力!如果本文对您有帮助,还请多多点赞👍、评论💬和收藏⭐!