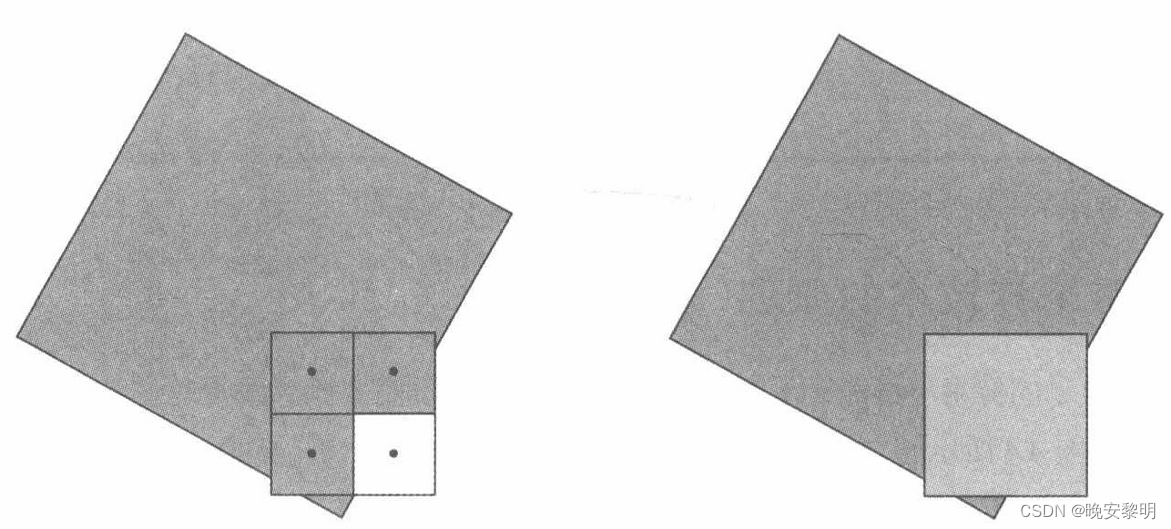
前言:不规则四边形的中心
不规则四边形的出心有多种定义,以下是最常见的三种:
1.重心:重心是四边形内部所有顶点连线交点的平均位置。可以通过求解四个顶点坐标的平均值来找到重心。
2.质心:质心是四边形内部所有质点的平均位置,质点可以看作是无限小的质量集中点。求解四个质点的质量,然后将质量乘以对应的坐标求和,再除以总质量,即可找到质心。
3.矩心:对于二维平面上的四边形,矩心是四边形内部所有顶点坐标的中点。可以通过求解四个顶点坐标的平均值来找到矩心。
需要注意的是,这些中心点并不一定在四边形的内部。例如,在凸四边形中,重心、质心和矩心三点通常不在同一位置,而在凹四边形中,这些中心点可能位于四边形的外部,在实际应用中,根据问题的需求和四边形的特性选择合适的中心点具有重要意义。
质心和重心虽然在某些情况下可能重合(如在均匀物体中),但它们并不是总是相同的。质心更多地关注于物体的质量分布,而重心则侧重于物体的重力作用及其平衡状态。
原理
要求计算多边形的质心,首先需要明确质心的定义:质心是多边形内所有点的平均位置。
在Matlab中,可以通过以下步骤计算多边形的质心:
- 步骤一:读取多边形数据。
将多边形的点坐标读入Matlab中。可以使用读取文本文件的命令,也可以手动输入点的坐标 - 步骤二:计算多边形的面积。
用到面积公式,根据点坐标通过行列式计算得到多边形面积值。 - 步骤三:计算多边形的重心(gravity center)。
重心的定义是多边形内各个三角形重心的面积加权求和。通过循环遍历多边形的各个三角形,计算每个三角形的重心,再将重心坐标值与其面积值相乘,最后累加到总重心坐标值上。 - 步骤四:计算多边形的质心(mass center)。
由于质心是所有点的平均位置,因此可以将总重心坐标值除以多边形的面积,得到多边形的质心坐标。
MATLAB代码
图形如下:

MATLAB代码如下:
clc
close all
clear
%% 主函数说明-MATLAB计算多边形质心示例
pathFigure= '.\Figures\' ;%% % 读取多边形点坐标
% x = [1 3 5 7 3 1];
% y = [1 1 3 8 3 6];x = [1 3 3 1];
y = [1 1 3 3];% 绘图1:绘制多边形形状
% ---------------------------------------------
pgon = polyshape( x , y );
A = area(pgon); % 计算多边形面积
P = perimeter(pgon); % 计算多边形周长
[Cx, Cy] = centroid(pgon); % 计算多边形矩心figure(1)
hold on; box on;
h1 = plot(pgon);
h(2) = plot(Cx, Cy,'o','Color',[255,61,0]/255,'Markersize',6);
axis equal; % 设置坐标系比例相等,保持正确显示多边形
set(gca,'FontSize',14,'FontName','Times New Roman'); str= strcat(pathFigure, "Fig.1", '.tiff');
print(gcf, '-dtiff', '-r600', str);