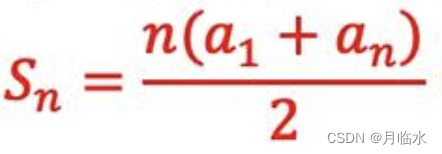---

每日一言

即使慢，驰而不息，纵令落后，纵令失败，但一定可以达到他所向往的目标。——鲁迅

---

题目

题目链接：找出中枢整数

给你一个正整数 n ，找出满足下述条件的 中枢整数 x ：

1 和 x 之间的所有元素之和等于 x 和 n 之间所有元素之和。
返回中枢整数 x 。如果不存在中枢整数，则返回 -1 。题目保证对于给定的输入，至多存在一个中枢整数。

• 示例 1：
  输入：n = 8
  输出：6
  解释：6 是中枢整数，因为 1 + 2 + 3 + 4 + 5 + 6 = 6 + 7 + 8 = 21 。

• 示例 2：
  输入：n = 1
  输出：1
  解释：1 是中枢整数，因为 1 = 1 。

• 示例 3：
  输入：n = 4
  输出：-1
  解释：可以证明不存在满足题目要求的整数。

提示：

1 <= n <= 1000

---

解题思路

1 和 x 之间的所有元素之和等于 x 和 n 之间所有元素之和。
运用等差数列求和公式把左右两式写出来
1 和 x 之间的所有元素之和：(x(x+1))/2
x 和 n 之间所有元素之和：(x+n)(n-x+1)/2

等差数列求和公式：

法一：

暴力解法
遍历1~n的所有数字，判断是否满足 (x(x+1))/2 = (x+n)(n-x+1)/2

法二：

用数学知识解决
化简等式
x^2=n(n+1)/2

代码

法一：

int pivotInteger(int n) {//x^2=n(n+1)/2int x = 0;for(x=1;x<=n;x++){if(((x+1)*x)/2 == (x+n)*(n-x+1)/2)return x;}return -1;
}

法二：

int pivotInteger(int n) {//x^2=n(n+1)/2int x = sqrt(n*(n+1)/2);if(x*x == n*(n+1)/2) return x;return -1;
}

---

结语

请给自己些耐心，一口吃不成胖子。
山外青山楼外楼，莫把百尺当尽头。
保持空杯心态加油努力吧！

---

都看到这里啦！真棒(*^▽^*)

可以给作者一个免费的赞赞吗，这将会鼓励我继续创作，谢谢大家

编程小白写作，如有纰漏或错误，欢迎指正

---