文章目录
- 一.二维差分
- 构造差分二维数组
- 二维差分算法
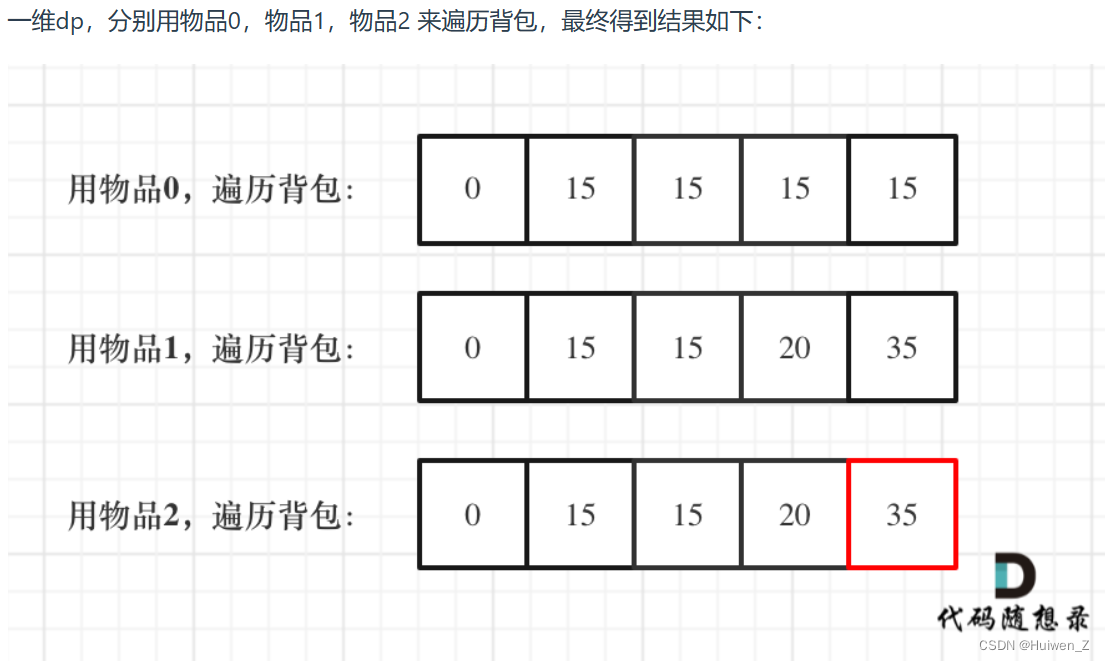
- 状态dp求b[i][j]数组的二维前缀和图解
- 二.三维前缀和与差分
- 三维前缀和图解:
- 三维差分核心公式图解:
- 模板题
一.二维差分
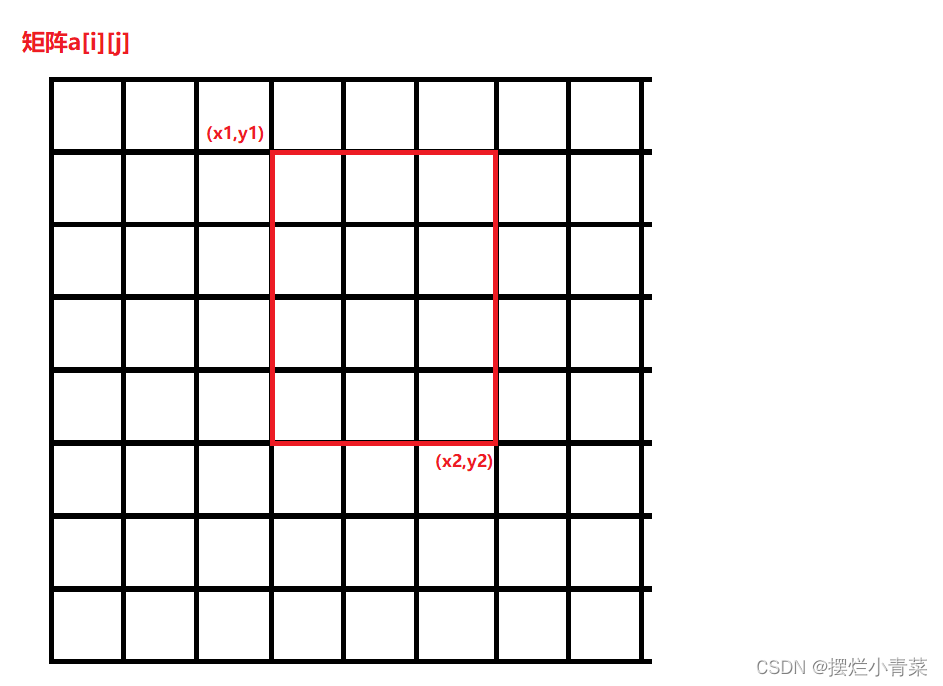
- 给定一个原二维数组
a[i][j],若要给a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c,暴力的做法时间复杂度为O(N^2),使用二维差分可以在O(1)的时间复杂度内完成该操作
构造差分二维数组
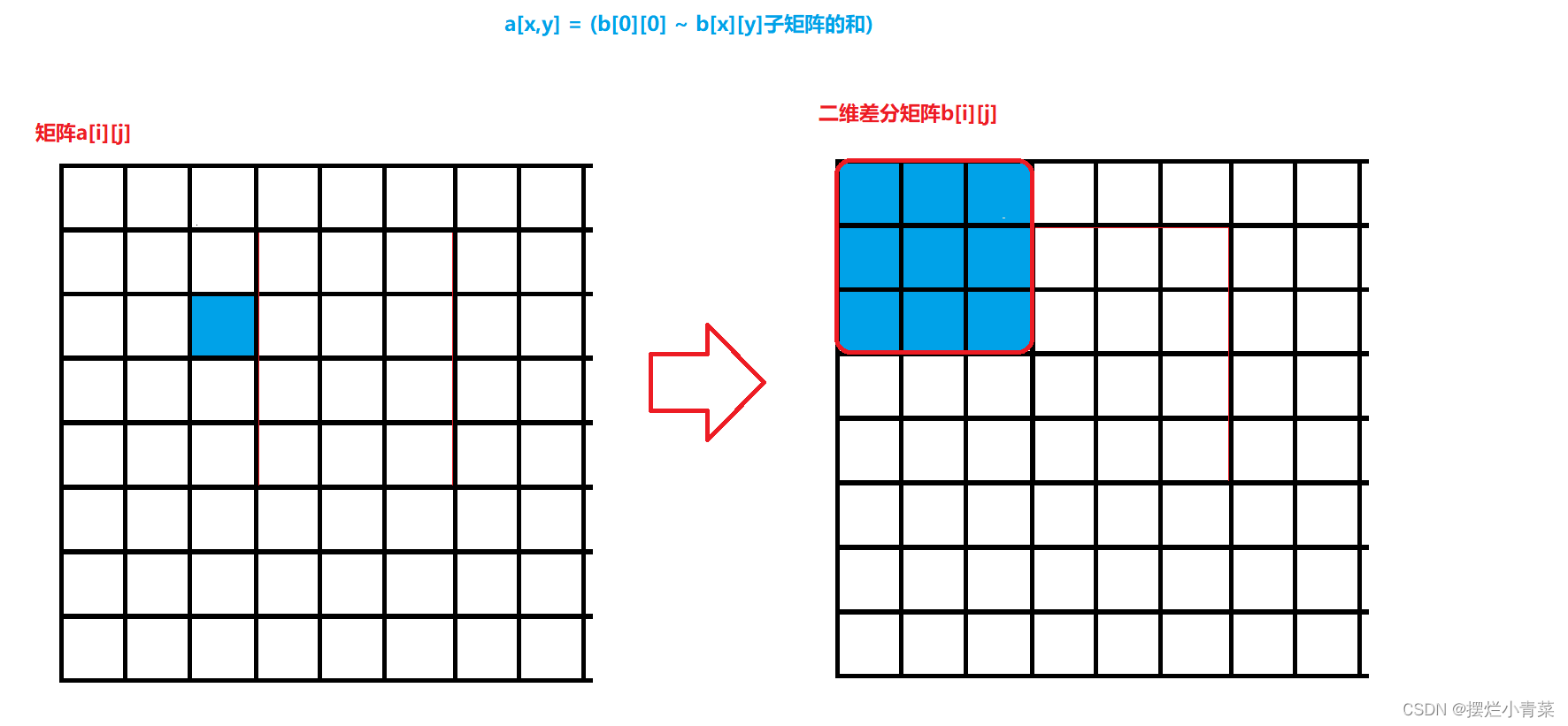
- 构造差分二维数组
b[i][j]使得原二维数组a[i][j]是二维数组b[i][j]的二维前缀和数组,即满足:
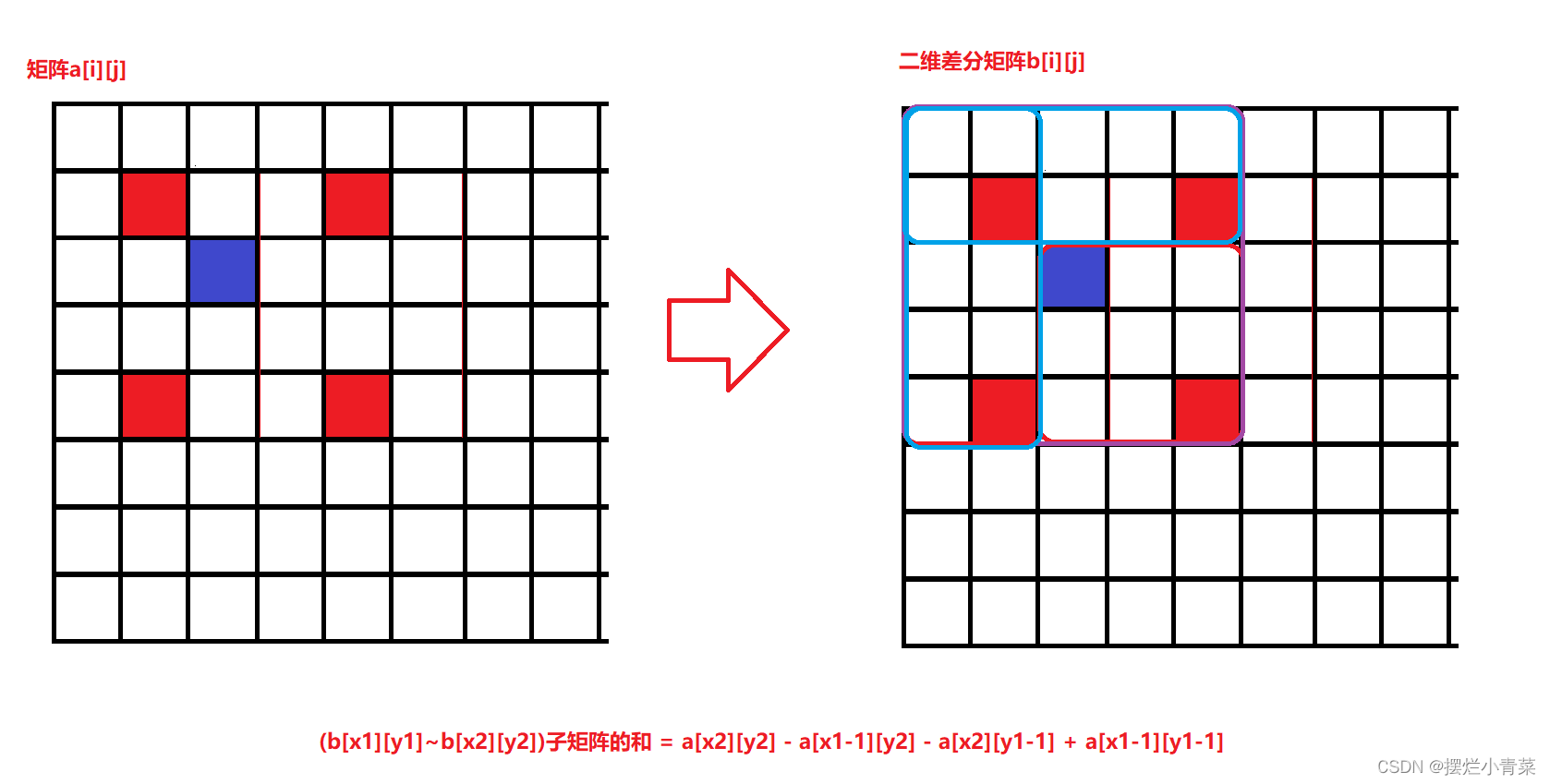
二维差分算法
- 若使原数组
a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c,等价于对b[i][j]数组进行如下操作:b[x1][y1] += cb[x2+1][y2+1] += cb[x2+1][y1] -= cb[x1][y2+1] -= c
- 核心操作接口:
//使原数组a[i][j]中以(x1,y1)和(x2,y2)为对角线的子矩阵中每个数都加上一个常数c
//接口可以用于构造差分矩阵以及进行原数组的矩阵元素整体修改操作
void Matrix_Add(long long(*b)[1010],int x1 ,int y1,int x2 ,int y2,int c){b[x1][y1] += c;b[x2+1][y2+1] += c;b[x1][y2+1] -= c;b[x2+1][y1] -= c;
}
//状态递推法对b[i][j]数组求二维前缀和,以获取原数组的元素--> 默认矩阵第0行第0列全部元素为0
void Get_Pre_Sum(long long(*b)[1010],int row , int col){//求(1,1)~(i,j)的子矩阵的和for(int i = 1 ; i <= row ; ++i){for(int j = 1 ; j<=col ; ++j){b[i][j] += (b[i-1][j] + b[i][j-1] - b[i-1][j-1]);}}
}- 求出
b[i][j]数组的二维前缀和就可以恢复原数组a[i][j]
状态dp求b[i][j]数组的二维前缀和图解
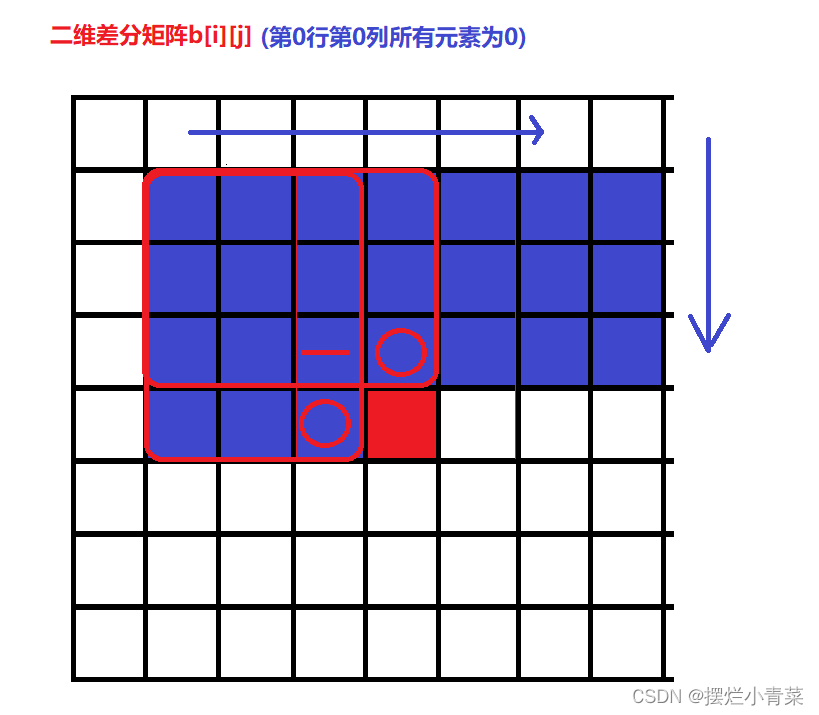
二.三维前缀和与差分
三维前缀和图解:
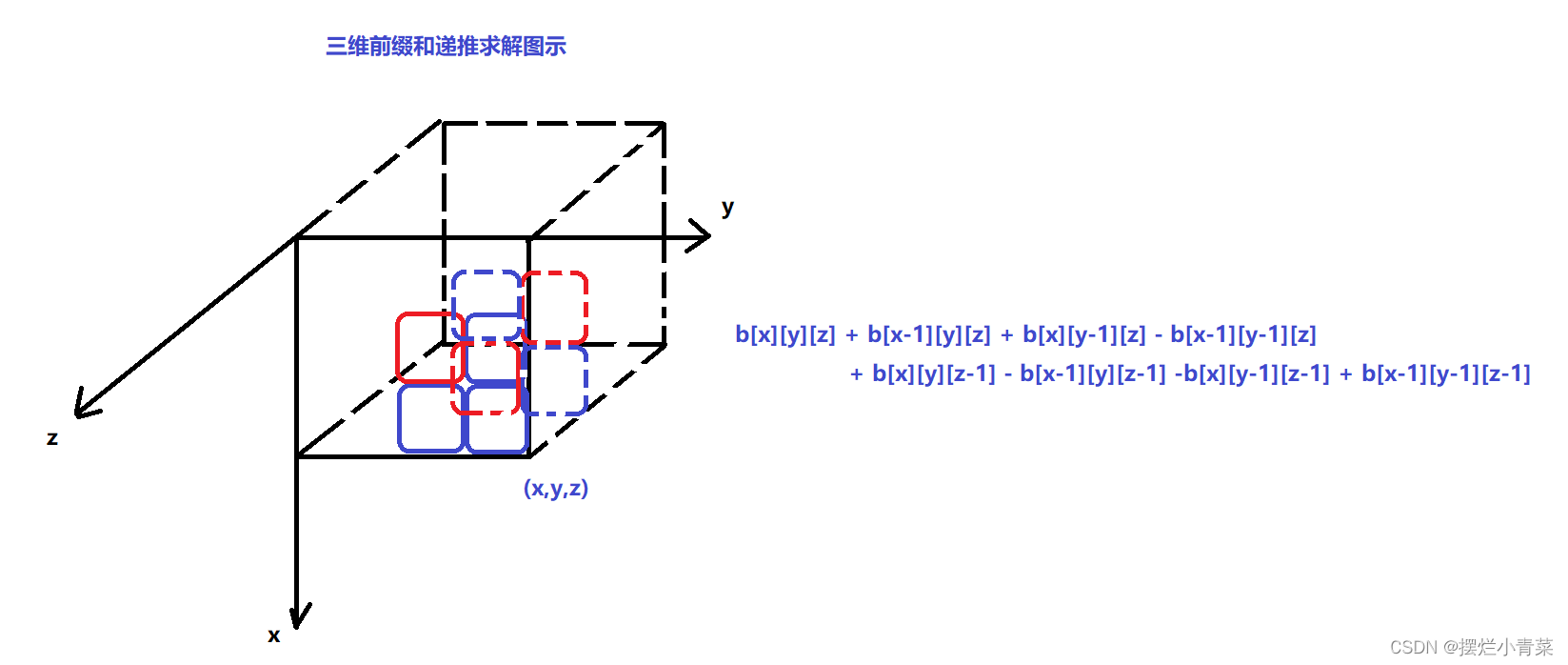
- 前缀和递推构造接口:
void Get_Pre_Sum(vector<vector<vector<long long>>>& Board,int high,int row,int col ){for(int i = 1 ; i <= high ; ++i){for(int j = 1 ; j <= row ; ++j){for(int k = 1 ; k <= col ; ++k){Board[i][j][k] += Board[i-1][j][k] + Board[i][j-1][k] - Board[i-1][j-1][k] +Board[i][j][k-1] - Board[i-1][j][k-1] - Board[i][j-1][k-1] + Board[i-1][j-1][k-1];}}}
}
三维差分核心公式图解:
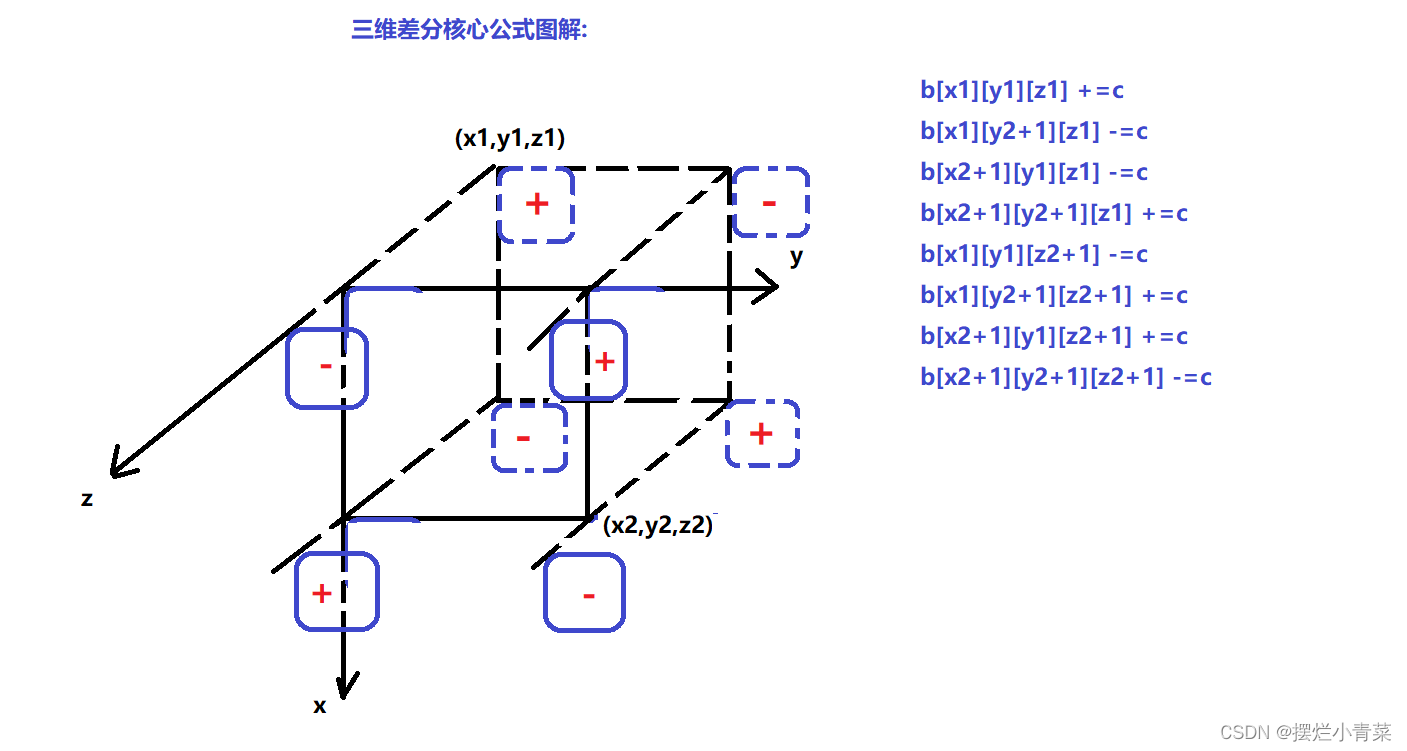
- "相邻点"的加减满足容斥关系,
相邻互斥,相间相容 - 核心公式接口:
void Matrix_Add(vector<vector<vector<long long>>>& Board,int x1 , int y1 , int z1 , int x2 , int y2 , int z2 , int c){Board[x1][y1][z1] += c;Board[x1][y2+1][z1] -= c;Board[x2+1][y1][z1] -= c;Board[x2+1][y2+1][z1] += c;Board[x1][y1][z2+1] -= c;Board[x1][y2+1][z2+1] += c;Board[x2+1][y1][z2+1] += c;Board[x2+1][y2+1][z2+1] -= c;
}模板题
差分模板题1
差分模板题2