一、题目

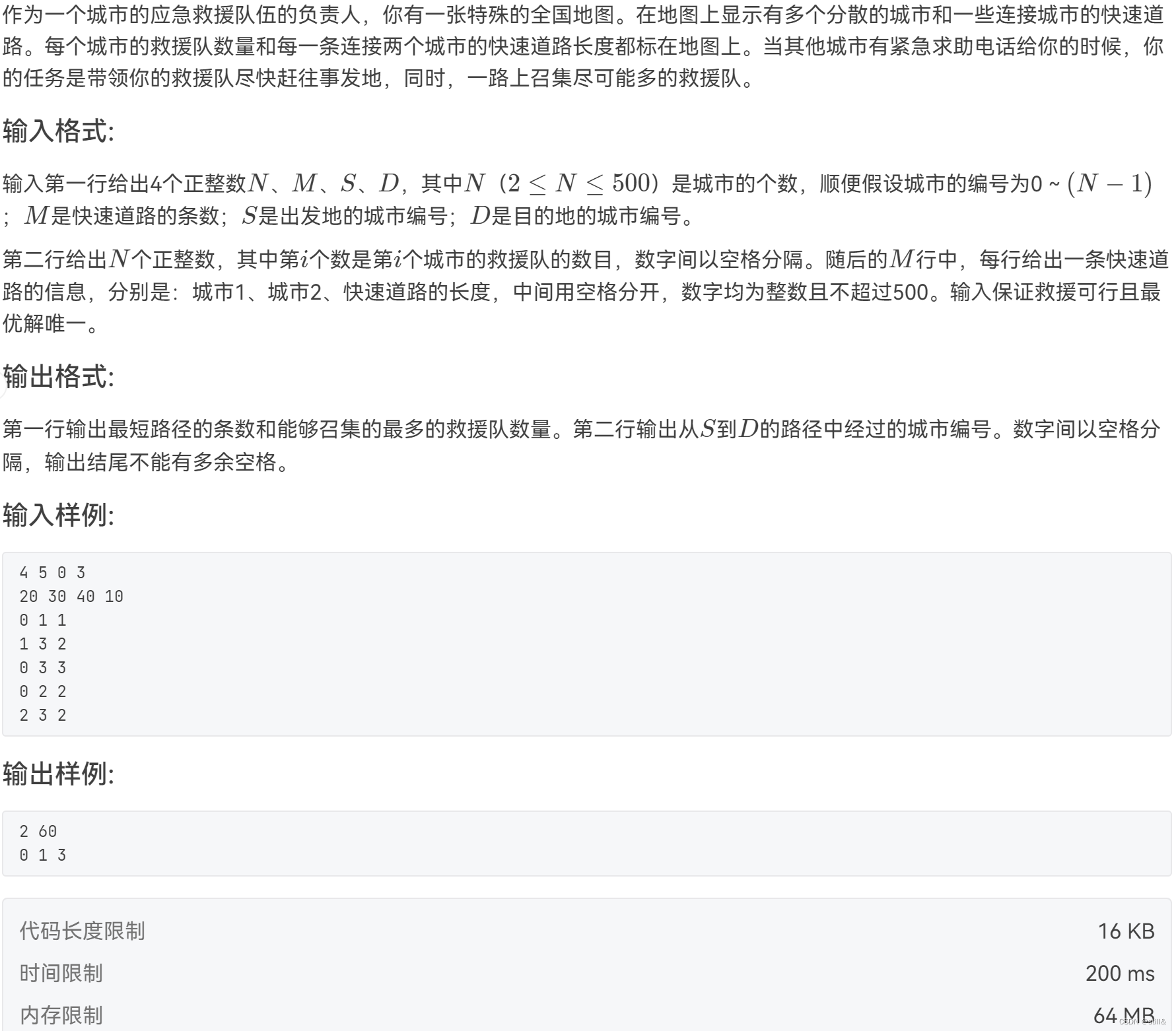
二、解题思路

1. 迪杰斯特拉算法。
2. 求最短路径的条数：在更新T时，如果是 dis[j]>dis[index]+map[index][j] ，则 cot[j]=cot[index] ，如果是 dis[j]==dis[index]+map[index][j] ，则 cot[j]+=cot[index] 。
3. 递归输出最短路径。

三、代码

#include<iostream>
using namespace std;
//无穷大 
#define maxInt 0x3f3f3f3f
//递归输出最短路径 
void printfPath(int end,int pre[])
{if(pre[end]!=-1){printfPath(pre[end],pre);cout<<" "<<end;}else{cout<<end;}
}
int main()
{int n,m,start,end;cin>>n>>m>>start>>end;
//	迪杰斯特拉的四个数组+三个数组 int map[n][n],flag[n],dis[n],pre[n],quan[n],army[n],cot[n];for(int i=0;i<n;i++){flag[i]=0;dis[i]=maxInt;pre[i]=-1;for(int j=0;j<n;j++){map[i][j]=maxInt;}cin>>quan[i];army[i]=0;cot[i]=1;}while(m--){int i,j;cin>>i>>j;cin>>map[i][j];map[j][i]=map[i][j];} 
//	起始节点 flag[start]=1;dis[start]=0;army[start]=quan[start];for(int i=0;i<n;i++){if(flag[i]==0){dis[i]=map[start][i];pre[i]=start;army[i]=quan[start]+quan[i];}}
//	其余节点 for(int i=1;i<n;i++){
//		找最小T int min=maxInt,index;for(int j=0;j<n;j++){if(flag[j]==0 && dis[j]<min){min=dis[j];index=j;}}flag[index]=1;
//		更新T for(int j=0;j<n;j++){if(flag[j]==0 && dis[j]>dis[index]+map[index][j]){dis[j]=dis[index]+map[index][j];pre[j]=index;army[j]=army[index]+quan[j];cot[j]=cot[index]; }else if(flag[j]==0 && dis[j]==dis[index]+map[index][j]){cot[j]+=cot[index];if(army[j]<army[index]+quan[j]) {dis[j]=dis[index]+map[index][j];pre[j]=index;army[j]=army[index]+quan[j];}}}}cout<<cot[end]<<" "<<army[end]<<endl;printfPath(end,pre);return 0;
}

四、总结

        是无向图，在构造图的矩阵时，cin>>map[i][j] ，要加上 map[j][i]=map[i][j] 。