题一:只出现一次的数字(1)

1.链接
136. 只出现一次的数字 - 力扣(LeetCode)
2.思想
- 借用位运算中异或操作符的特点,a^a=0,0^a=a
- 先定义一个sum=0
- 就用一个循环来遍历这个数组,每次都进行 sum ^ = nums[i]
- 当循环结束,那么此刻sum里就是正确答案
3.代码
class Solution {
public:int singleNumber(vector<int>& nums) {int result=nums[0];for(int i=0;i<nums.size()-1;i++){result=result^nums[i+1];}return result;}
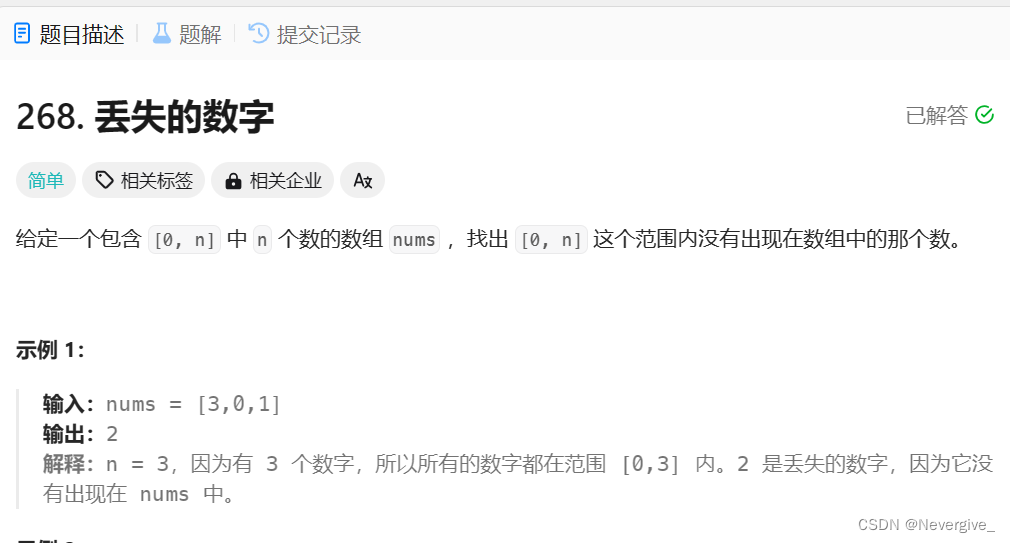
};题二:丢失的数字
1.链接
268. 丢失的数字 - 力扣(LeetCode)
2.思路
- 借用位运算中异或操作符的特点,a^a=0,0^a=a
- 先定义一个变量sum,并初始化为0
- 然后在利用一个for循环来处理,每次循环都进行 sum^=i 的操作
- 在去遍历整个数组,遍历时,进行sum^=nums[i]的操作
- 最终sum就是要找的那个值
3.代码
class Solution {
public:int missingNumber(vector<int>& nums) {int sum=0;for(int i=1;i<=nums.size();i++){sum^=i;}for(int i=0;i<nums.size();i++){sum^=nums[i];}return sum;}
};题三:只出现一次的数字 (2)

1.链接
137. 只出现一次的数字 II - 力扣(LeetCode)
2.思路
位图的思想
前提:我们让出现一次的数为:a,出现三次的数统称为b;
- 由于数据的特殊性,我们可以统计这些数据用二进制表示时,每个位数出现一的个数
- 判断,该位数是出现1的个数。a 的二进制在该位数时的结果是0或1,而 b 的二进制在该位数时的结果:3的倍数或者0
- 则统计各个位数出现1的结果则可能是:0+3的倍数,1+3的倍数,0+0,0+1
- 此时,我们可以对其进行%3的操作,结果等于1,那么则就代表a在这个位是1
- 当%3的操作,结果等于1,那么则就将数字在该位修改为1
由于数据范围是:- 2 的31次方——2 的 31 次 方 - 1,那么数据类型为int,就可以进行位图思想
3.代码
class Solution {
public:int singleNumber(vector<int>& nums) {int ret = 0;for (int i = 0; i < 32; i++) {int sum = 0;for (auto x : nums)if (((x >> i) & 1) == 1)sum++;sum = sum % 3;if (sum == 1)ret |= (1 << i);}return ret;}
};题四:只出现一次的数字 (3)

1.链接
260. 只出现一次的数字 III - 力扣(LeetCode)
2.思路
先定义一个int类型的变量 sum ,并初始化为0
- 先遍历这个数组,并进行 sum ^ = nums[ i ]的操作
- 完成遍历操作后,得到的其实就是:二个只出现一次的数,进行异或的结果(sum)
- 考虑异或的性质,相同为0,相异为1,sum的二进制表示中从左往右出现的第一个1,就是二个只出现一次的数 的二进制表示形式 的第一个不同处
- 我们可以进行 sum & (-sum)的操作,这样就得到了从左往右出现的第一个1( rs ),并且其它位全为0
- 然后对数据进行分组处理,按照nums [ i ] & rs 等于0 和 不等于0 进行处理
- 当不等于0时,对数据进行 tmp ^ = nums[ i ]的操作,最终 tmp就是二个只出现一次的数的其中之一
- 然后再将 sum ^ tmp , 就得到了另外一个数
3.代码
class Solution {
public:vector<int> singleNumber(vector<int>& nums) {long long sum = 0;for (int j = 0; j < nums.size(); j++) {sum ^= nums[j];}long long rs = sum & (-sum);int tmp = 0;for (int j = 0; j < nums.size(); j++) {if (nums[j] & rs)tmp ^= nums[j];}int b=sum^ tmp;return {tmp, b};}
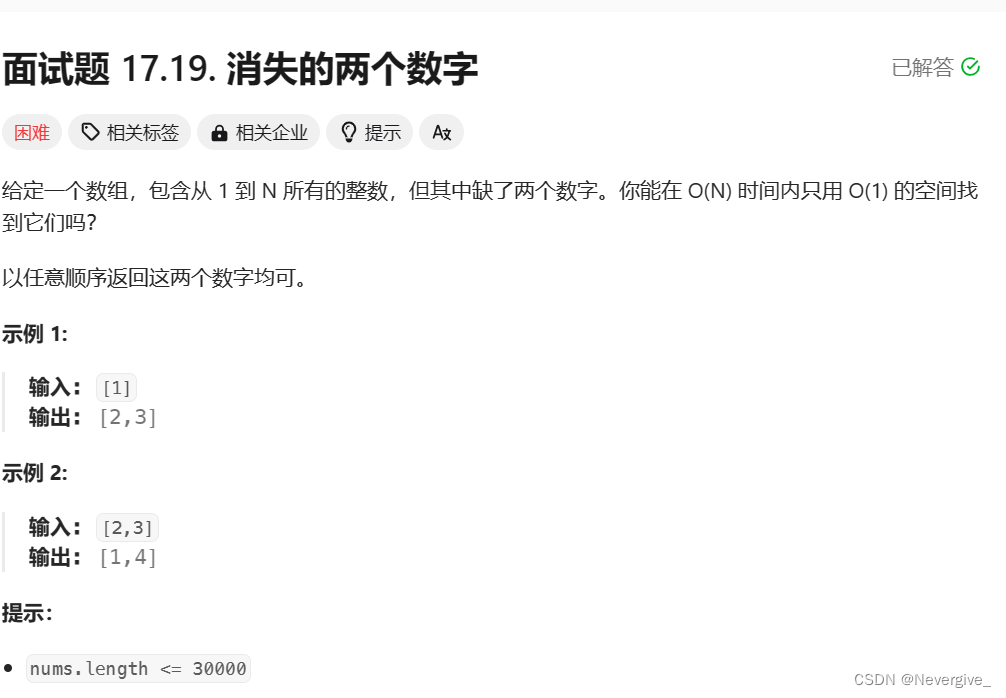
};题五:消失的两个数字(消失的数字的综合题)
1.链接
面试题 17.19. 消失的两个数字 - 力扣(LeetCode)
2.思路
总体思路是:
- 这个问题可以转化为题四,这里其实就是一组数据,其中只有二个数据只出现一次,其它都出现二次
- 那么就可以,找到只出现一次的二个数据再二进制表示时,第一个不同的位置
- 然后根据这个为依据,进行分组处理(处理的思路,就是题1)
3.代码
class Solution {
public:vector<int> missingTwo(vector<int>& nums) {int n = nums.size();int ret = 0;for (int i = 1; i <= n + 2; i++) {ret ^= i;}int sum = 0;for (int i = 0; i < n; i++) {sum ^= nums[i];}int rsum = ret ^ sum;int rs = rsum & (-rsum);int tmp = 0, rtmp = 0;for (int i = 0; i < n; i++) {if (nums[i] & rs)tmp ^= nums[i];else {rtmp ^= nums[i];}}for (int i = 0; i <= n + 2; i++) {if (i & rs)tmp ^= i;elsertmp ^= i;}return {rtmp, tmp};}
};