宽带高效非对称连续J/F-1模式Doherty 功率放大器设计(2023.11 MTT)-从理论到ADS版图-编程知识

宽带高效非对称连续J/F-1模式Doherty 功率放大器设计(2023.11 MTT)-从理论到ADS版图

这个文章实现的效果非常好，非常值得大家去阅读复现（见前言介绍），但是我复现出现了一点困难，效果调不到那么好（带宽只是原来的三分之一）。

工程免费下载：https://download.csdn.net/download/weixin_44584198/88831515

原文: Continuous Class-J/F−1 Mode Asymmetrical Doherty Power Amplifier With Extended Bandwidth and Enhanced Efficiency
发表于NOVEMBER 2023，在微波顶刊IEEE T MTT上面，使用的GAN CGH40010F和GAN CGH40025

0、前言

这个文章中实现的效率和回退效果是非常的好，但是我自己的复现非常强差人意，我复现的时候基本搞清楚了文中的理论计算什么的，也基本按照要求实现了阻抗，但是效果还是很差，懂行的朋友可以一起研究下，最上方下载链接有全部的文件。

至于为什么不直接使用作者给出的原理图进行复现呢？老问题，原理图画的和实物图对不上，哪怕是另一个基于连续相位负载调制的单输入宽带混合Doherty功率放大器设计我复现的比较好，它原理图和实物图也是对不上的，不知道是不是这些作者喜欢留一手。

这篇文章的后匹配PMN明显是对不上的：
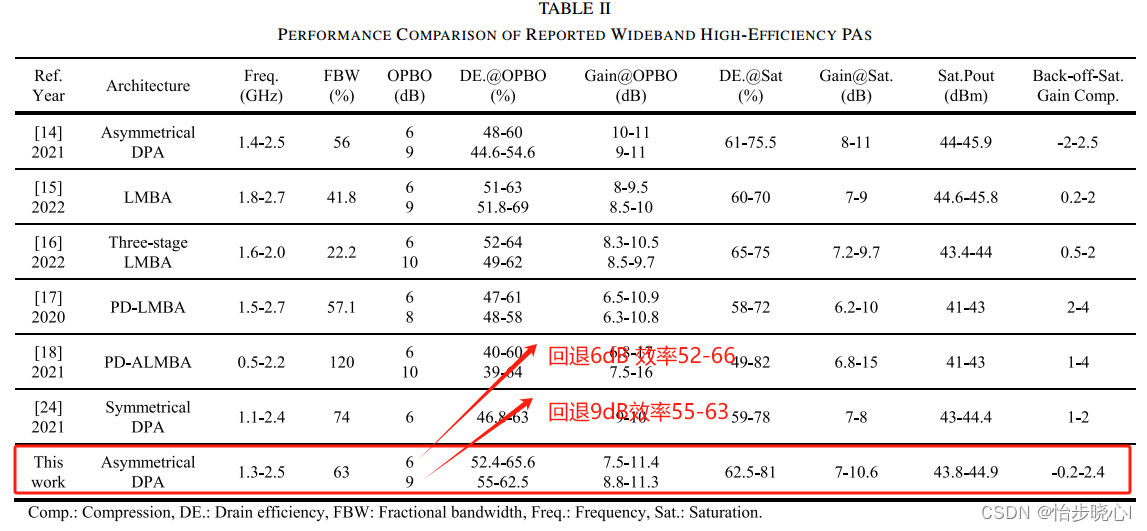
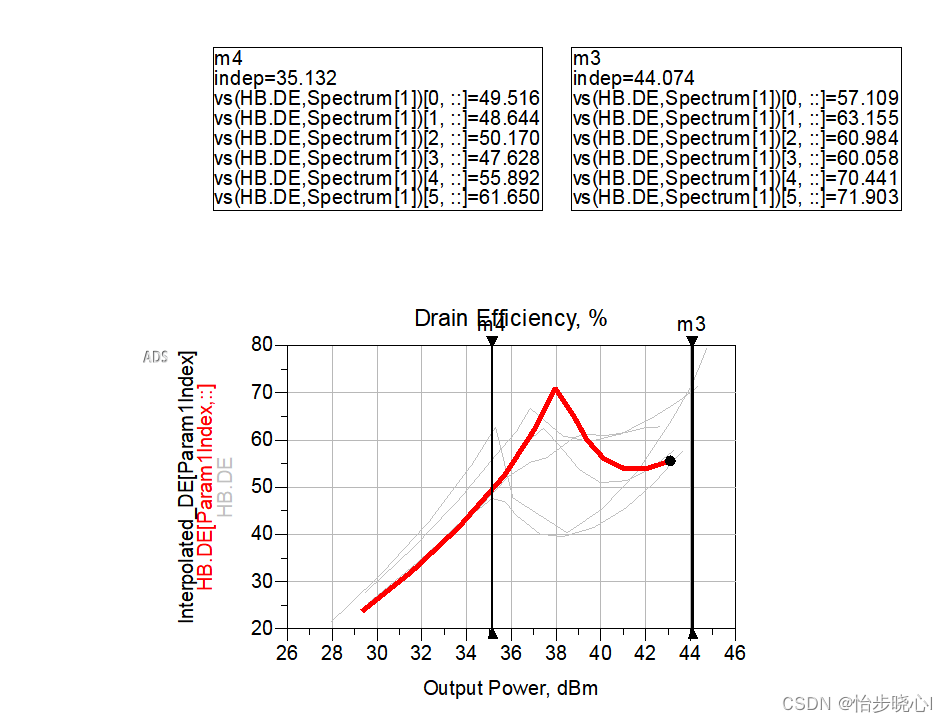
在这里插入图片描述

给大家贴出一下这篇文章实现的效果，哪怕回退9db效率还在55%以上，也是因为这个我对复现这个文章是非常感兴趣的，相信各位朋友也是：
在这里插入图片描述
我自己仿真（自己按照作者理论调的）实现的效果（见笑了，比较差，1.6-2.3GHz，9dB回退效率也能到50%左右吧，峰值效率60%-70%左右，其他频率更加难看就不说了）：

1、文章的核心思路

这是一个非对称的高回退的DPA设计，这种非对称设计对回退dB的改进非常大，非对称的高回退理论可以参考：理想架构的非对称高回退Doherty功率放大器理论与仿真。文中两个管子分别是13W的CGH40010F和25W的CGH40025F。

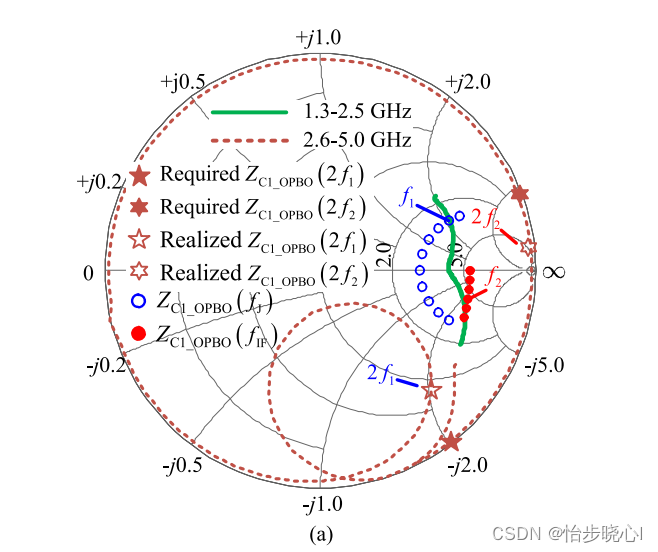
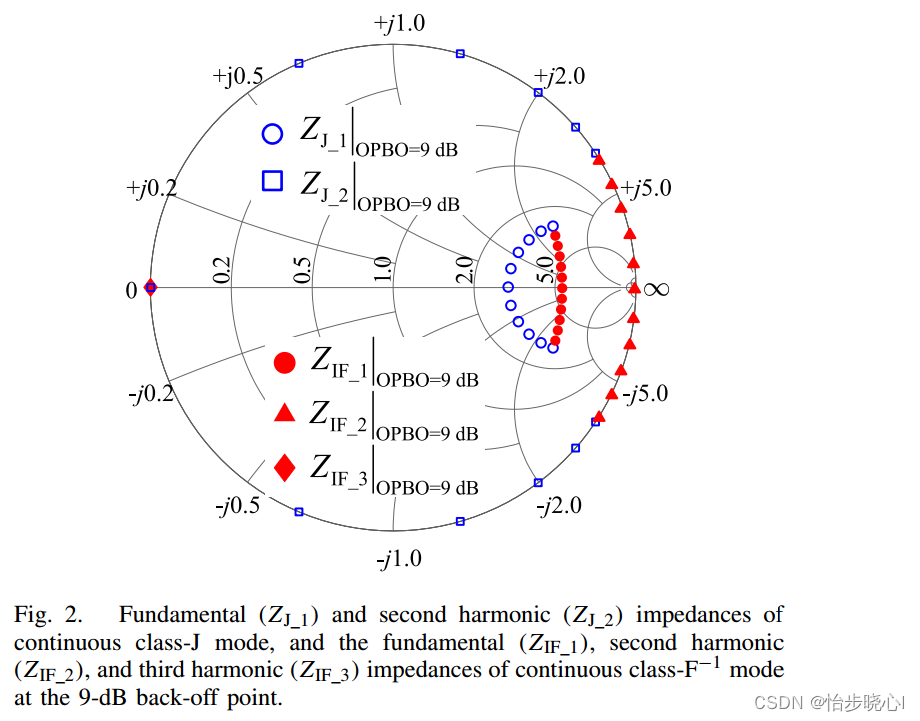
连续J/F-1模式指的是载波功放工作在回退状态下的工作模式，峰值功放在饱和时的工作模式没有详细介绍（我猜测应该是B类？）。如下图可见，蓝色就是回退时连续B/J类的设计空间、红色的是回退时连续F-1的设计空间，绿色和棕色是作者设计的阻抗控制。

从连续空间来说并不特别，作者的突出贡献是提出了一种结构来实现这样的阻抗控制，从载波功放的连续阻抗要求推导了峰值支路的设计和后匹配网络PMN的阻抗要求。

令我眼前一亮的载波功放的谐波控制（下面图的棕色部分），控制的非常好了，可能是理论推导带来的巨大优势。我DPA看的国外文章不是特别特别多，没见过啥世面，我把这个和史伟民博士毕业论文的连续DPA的谐波控制对比了一下，确实好不少的（当然那个毕业论文都快是十年了都）。
在这里插入图片描述

2、理论推导

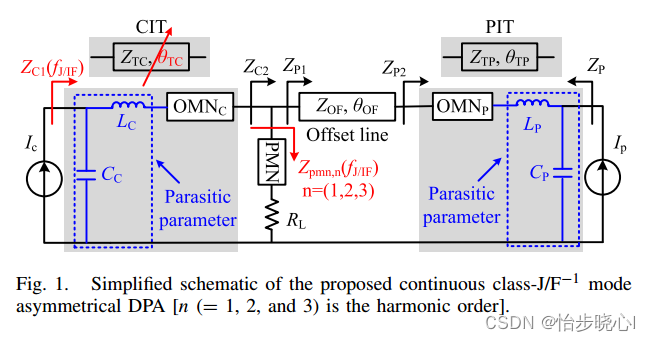
2.1、DPA架构

文中考虑了封装参数，直接把载波功放和其匹配电路等效成了微带线ZTC，峰值功放和其匹配电路等效成了微带线ZTP。文中的求解进行了大量的假设，首先是假设峰值功放到合路电的延迟是180°，这样在回退时的中心频率ZP1是由于阻抗变换特性处于开路状态，进而 $\theta_{TP}$ 和延迟线 $\theta_{OF}$ 都被假设成在中心频率处90°。
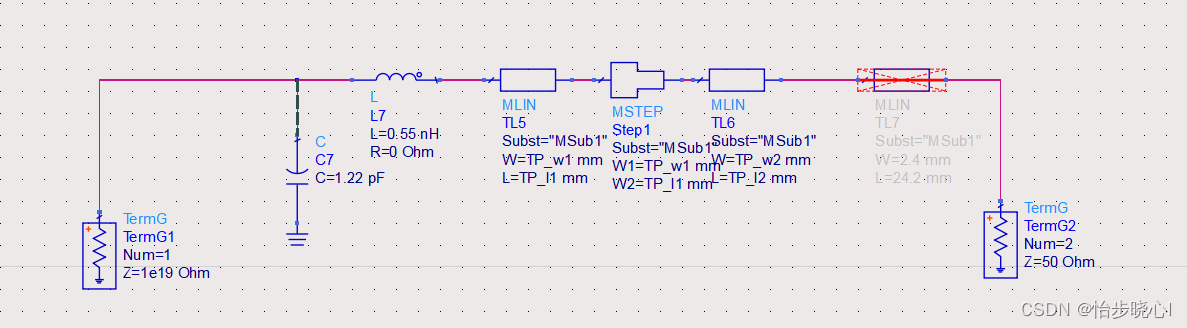
在这里插入图片描述

2.2、 $\theta_{TP}$ 和 $\theta_{OF}$ 实现

对于 $\theta_{OF}$ 被假设成在中心频率处90°，直接使用在中心频率为90°电长度的微带线即可，而带有封装参数的 $\theta_{TP}$ ，使用作者给出的电路也可以差不多的仿真出来（原理图OutputMatch_Raw_TP）：
在这里插入图片描述

2.4、连续J/F-1模式的设计空间

重点来了，为了实现连续模式，需要先获得单点的阻抗，如何直接使用现有的连续公式计算连续的基波、谐波阻抗。因此，需要先确定回退dB数，进而确定功率分配比和回退阻抗点，作者也是直接给出了公式：
$\begin{aligned} & K=10^{\left(\frac{\mathrm{OPBO}}{-20}\right)} \\ \text{}& \alpha=\left|\frac{I_{p,\operatorname*{max}}}{I_{c,\operatorname*{max}}}\right|=\frac{1}{1}-1 \\ \text{ZOF}& =\frac{Z_\mathrm{TC}Z_\mathrm{TP}}{R_\mathrm{opt}} \\ Z_{\mathrm{pmn}}& =\frac{KZ_{\mathrm{TC}}^2}{R_{\mathrm{opt}}} \\ Z_{C1\_\mathrm{OPBO}}(f_0)& =\frac{Z_{\mathrm{TC}}^2}{Z_{\mathrm{pmn}}}=\frac1KR_{\mathrm{opt}} \end{aligned}$

连续B/J类的拓展也是非常的简单，套现在的公式就行：
$\begin{cases}Z_{1f,C-B/J}=(1+j\gamma)R_{opt}\\Z_{2f,C-B/J}=-j\frac{3\pi}8R_{opt}\\Z_{nf,C-B/J}=\infty&\end{cases}$

因此目标空间就是：
$\begin{aligned}Z_{\mathrm{J}_{-1}}&=(1+\gamma j)Z_{\mathrm{C}1\_\mathrm{OPBO}}(f_0)\\Z_{\mathrm{J}_{-2}}&=-j\gamma\frac{3\pi}8Z_{\mathrm{C}1\_\mathrm{OPBO}}(f_0)\end{aligned}$

对于IF类，也是类似的操作。但是值得注意，要输出相同的功率，IF类的阻抗是B/J类的两倍（参考浅谈连续逆F类的基础理论-波形、最佳阻抗、输出功率）。由此可以确定IF类的设计空间，那么简单的两者混合的设计空间为：
在这里插入图片描述

2.3、 $\theta_{TC}$ 的推导与实现

对于上面那么多的公式，我们需要首先确定ZTC和ZTP，确定完其他的就都可以算出来了。那么ZTC和ZTP如何确定讷？没有公式，只能随便选，然后选计算出来理论效率最高的（作者分析了Case1，Case2什么的举例）。

作者最终设计选的是ZTC=2.3Ropt，ZTP=0.67Ropt，当然这个理论效率的计算会在附录给出相关代码。ZTC=2.3Ropt，ZTP=0.67Ropt假定之后，我们可以直接算出ZOF、Zpmn，进而计算出ZC2。算出来的ZC2实际上就是一个连续的阻抗点，如：
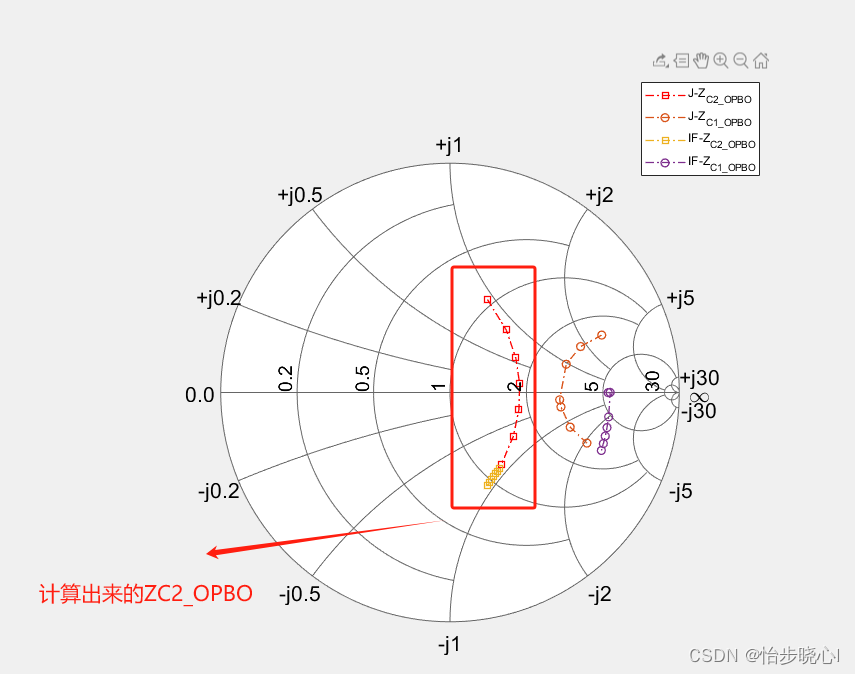
在这里插入图片描述
但是我们假设的ZC1_OPBO是上图右边的橙黄色和紫色，那么就需要把橙黄色和紫色所代表的连续空间变换到ZC2_OPBO。这两个阻抗之间差的就是一个 $\theta_{TC}$ ，所以我们要争对每个点都找 $\theta_{TC}$ 去将阻抗进行变换。

这个 $\theta_{TC}$ 我无法进行解析计算，因此使用了非线性规划求数值解，简单理解就是争对每个阻抗点遍历 $\theta_{TC}$ （代码见附录），直到找到一个能够完美变换的，计算得出的结果和文中基本一致：
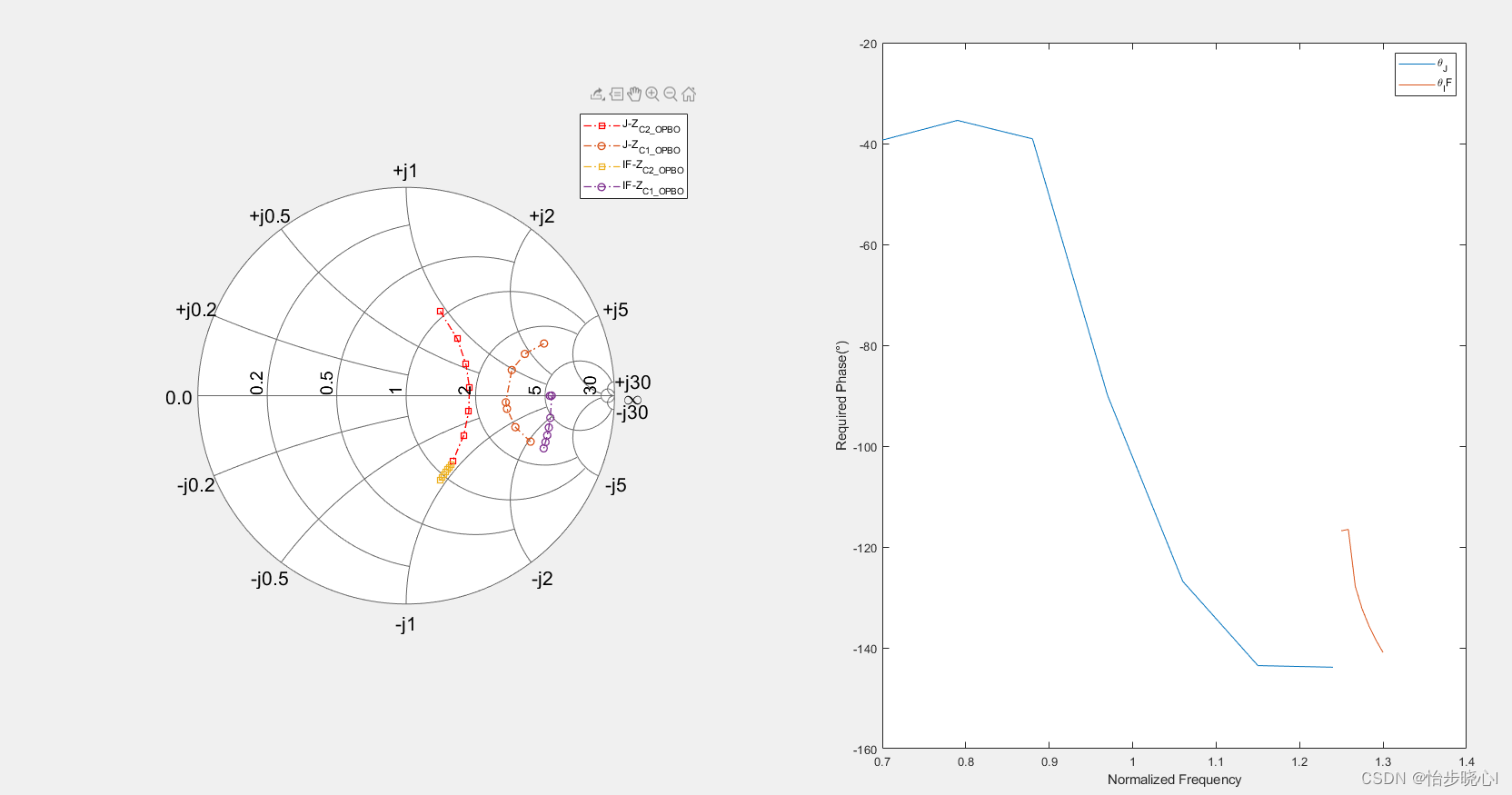
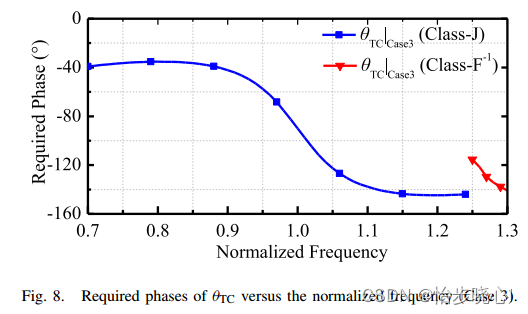
在这里插入图片描述

这个非线性相位无法实现，作者使用了等效，但是我觉得这个差很大：

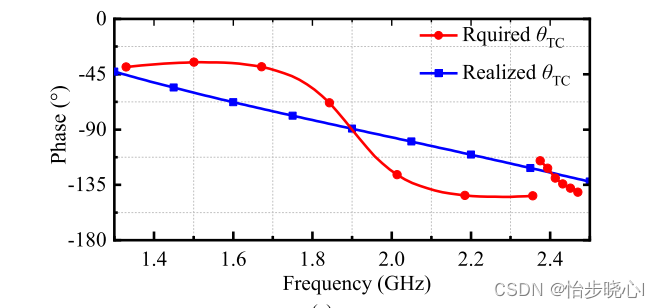
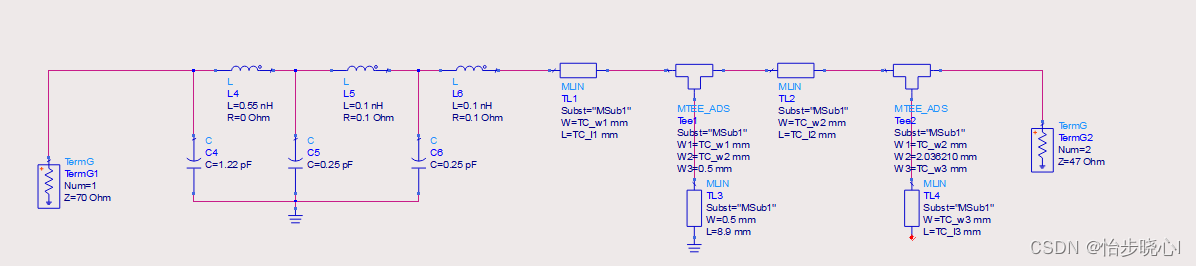
我自己使用ADS和作者提供的原理图对这个 $\theta_{TC}$ 的延迟进行仿真，和作者图片相差不大：

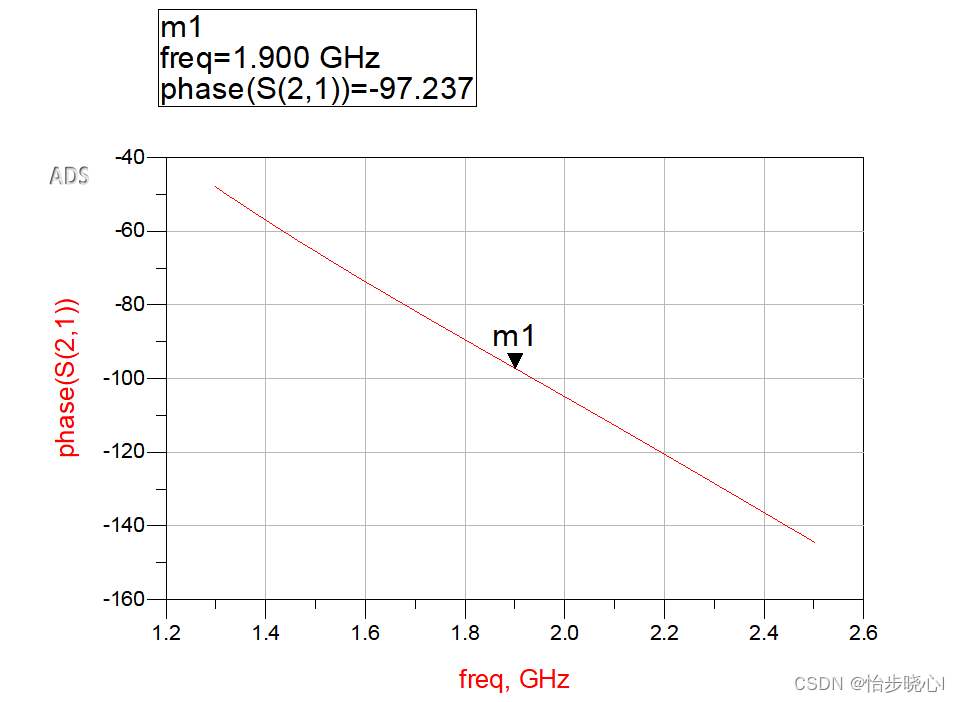
2.4、理论效率的计算

作者给出了理论效率的计算公式：
$P_{\mathrm{OUT,C}}=\begin{cases}\frac{1}{2}\frac{V_{\mathrm{DD}}^2}{\left|Z_{C1\_\mathrm{SAT}}\right|^2/\mathrm{Re}(Z_{C1\_\mathrm{SAT}})},&|Z_{C1\_\mathrm{SAT}}|\geq R_{\mathrm{opt,C}}\\\frac{1}{8}|I_{c,\max}|^2|Z_{C1\_\mathrm{SAT}}|,&|Z_{C1\_\mathrm{SAT}}|<R_{\mathrm{opt,C}}\end{cases}$

$P_{\mathrm{OUT,P}}=\frac14|I_{p,\max}|V_{\mathrm{DD}}$

$P_{\mathrm{dc}}=\frac1\pi V_{\mathrm{DD}}(\left|I_{p,\max}\right|+\left|I_{c,\max}\right|)$
$\eta_{\mathrm{SAT}}=\frac{P_{\mathrm{OUT,C}}+P_{\mathrm{OUT,P}}}{P_{\mathrm{dc}}}$

我之间写成了Matlab计算，见附录，得到的结果为：
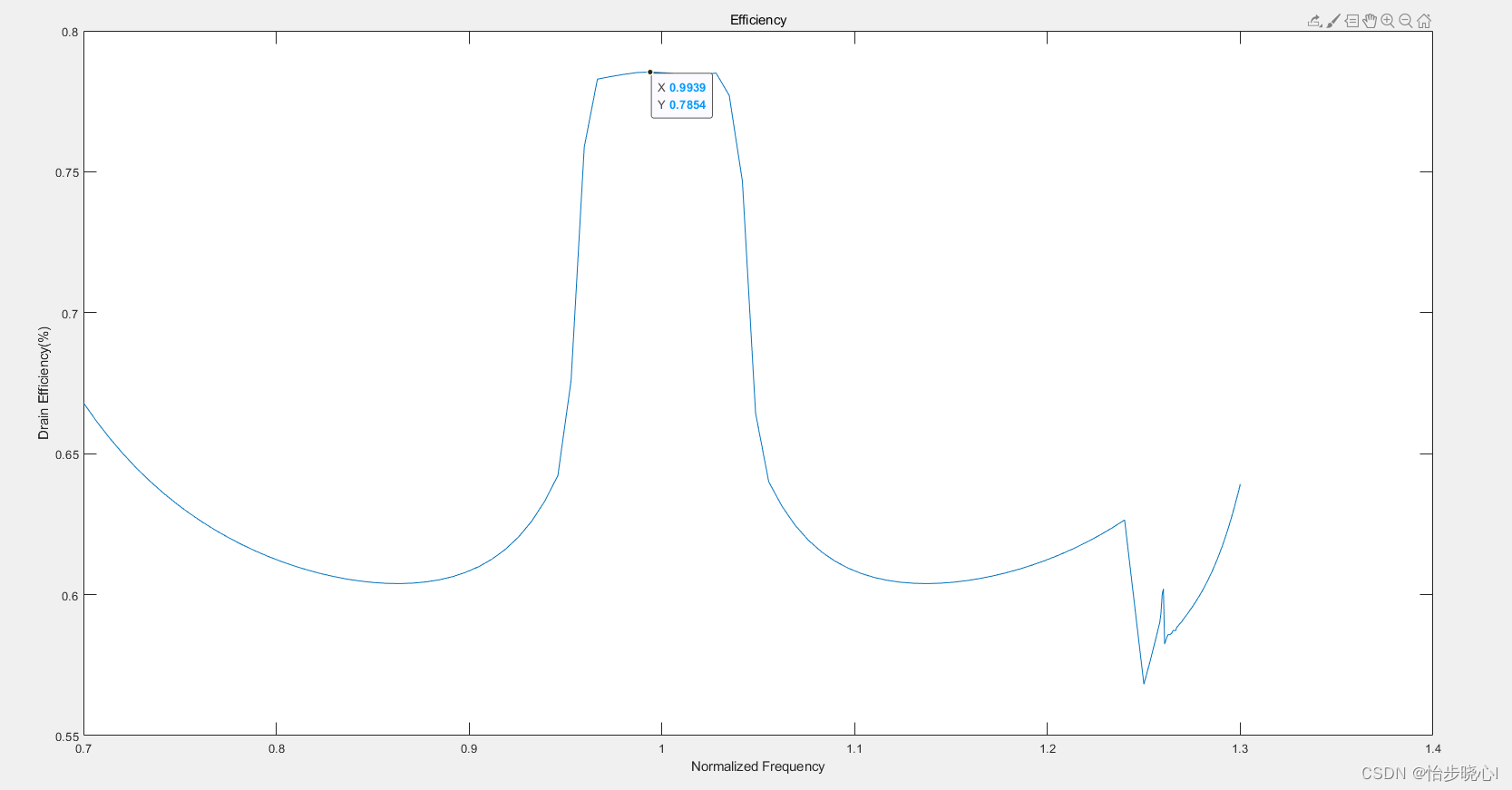
在这里插入图片描述
作者的结果和我不太一致，可能作者点数比较少，然后平滑插值的？但是大差不差：

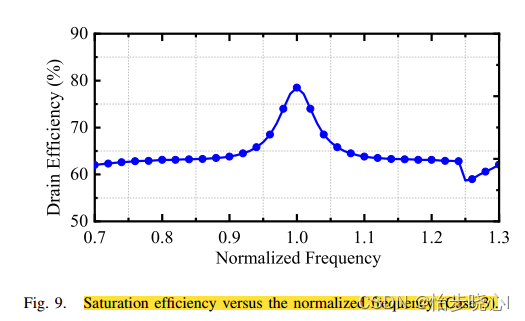
2.5、Zpmn的谐波控制设计

基于ZC1_OPBO所需的谐波阻抗，结合微带线推导计算，可以得出Zpmn的理论谐波控制阻抗，如公式（代码见附录）：
$Z_{C2\_\mathrm{OPBO},2}(2f_{\mathrm{JIF}})=Z_{\mathrm{TC}}\frac{Z_{C1\_\mathrm{OPBO},2}(2f_{\mathrm{JIF}})-jZ_{\mathrm{TC}}\tan(2\theta_{\mathrm{TC}})}{Z_{\mathrm{TC}-j}Z_{C1\_\mathrm{OPBO},2}(2f_{\mathrm{JIF}})\mathrm{tan}(2\theta_{\mathrm{TC}})}$

$\begin{gathered} Z_{\mathrm{pmn},2}(2f_{\mathrm{J}}) =\frac{Z_{C2\_\text{OPBO},2}(2f_{\mathrm{J}})Z_{P1\_\text{OBPO}}}{ Z _ { P 1 \_\text{OBPO}} - Z _ { C 2 \_\text{OPBO},2}(2f_{\mathrm{J}})} \\ Z_{\mathrm{pmn},2}(2f_{\mathrm{IF}}) =\frac{Z_{C2\_\mathrm{OPBO},2}(2f_{\mathrm{IF}})Z_{P1\_\mathrm{OBPO}}}{Z_{P1\_\mathrm{OBPO}}-Z_{C2\_\mathrm{OPBO},2}(2f_{\mathrm{IF}})} \end{gathered}$

三次谐波也是依次类推了。

2.6、中心频率的理论仿真

对于非中心频率，作者只计算了效率，没有分析电压、电流的具体行为（非中心频率我仿真不出来效果）。因此我只能对中心频率进行理论的仿真（原理图F_100）。当然，里面的参数都是基于作者的计算：
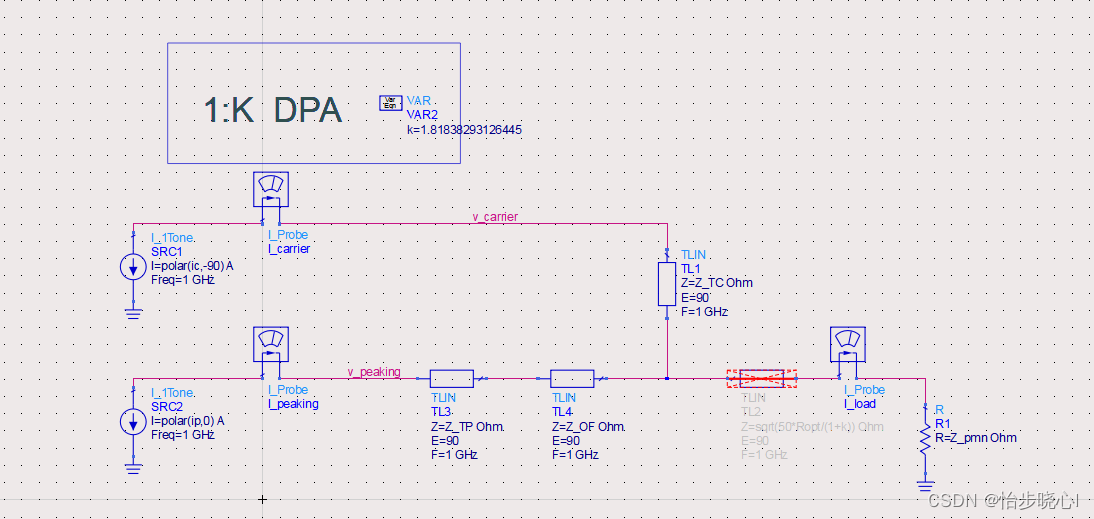
在这里插入图片描述
各个部件的参数如下：

3、ADS的具体实现

作者的实现和理论的推导有一些差异。

分析的时候回退数设置在了9dB，这样计算出来的分配比 $\alpha$ 应该是1：2.2左右。但是作者最终设计使用的功分器的分配比为1：1.5，这对应的回退是OPBO=8。如果要设计OPBO=8的，为什么之前分析为什么要设定OPBO=9呢？先不管那么多了

作者的Zpmn设置为1.4Ropt，实际应该使用1.8Ropt左右。1.4Ropt差不多对应OPBO=11.3时候的理论值，一致性比较差。这可能是调谐后的结果（可能是为了谐波控制）。其他一些阻抗上的调谐就不额外说明了。

3.1 Zpmn匹配电路设计

OutputMatch_pmn原理图，Zpmn主要是在谐波和基波有要求，基波匹配到36欧姆附近，作者pmn实物和原理图有差异，我使用我自己优化的。差不太多：
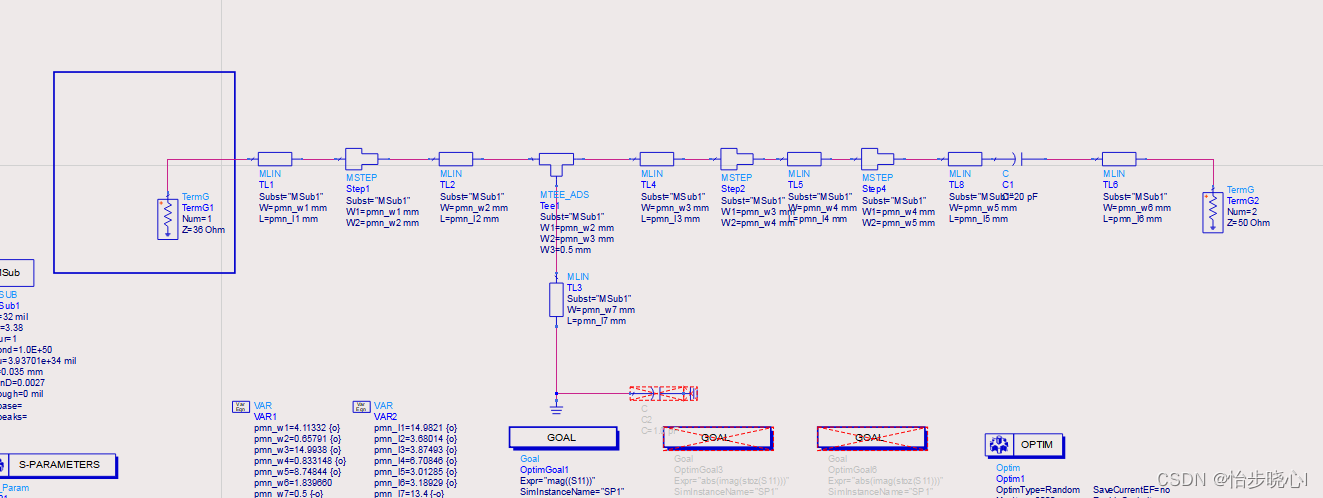
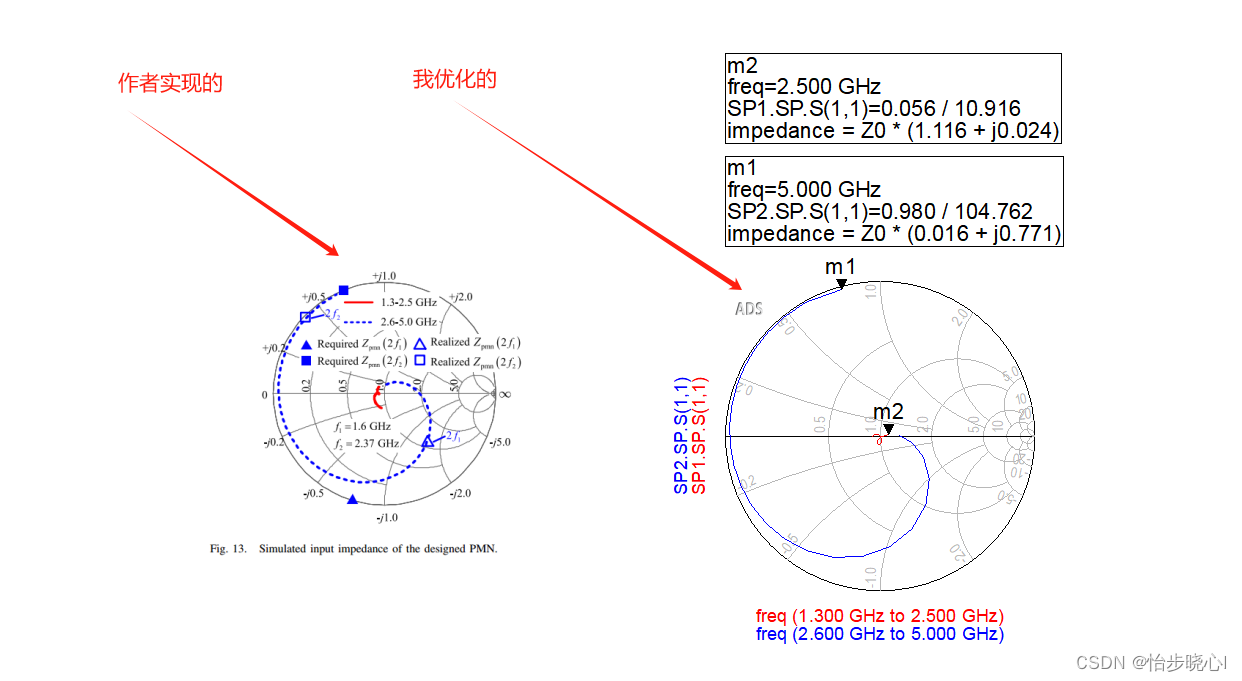
在这里插入图片描述

在这里插入图片描述

3.2 合路电路的优化

OutputMatch_Raw原理图，使用作者原来原理图给出的合路电路仿真结果比较差，可能是精度不够的问题。我自己设置目标进行优化，最后得到的电路和效果如下（此处是原理图的结果，版图没调，之后的整个系统仿真的输出匹配合路也先使用原理图的结果，因为这个和理论要求的一致性比较好）：
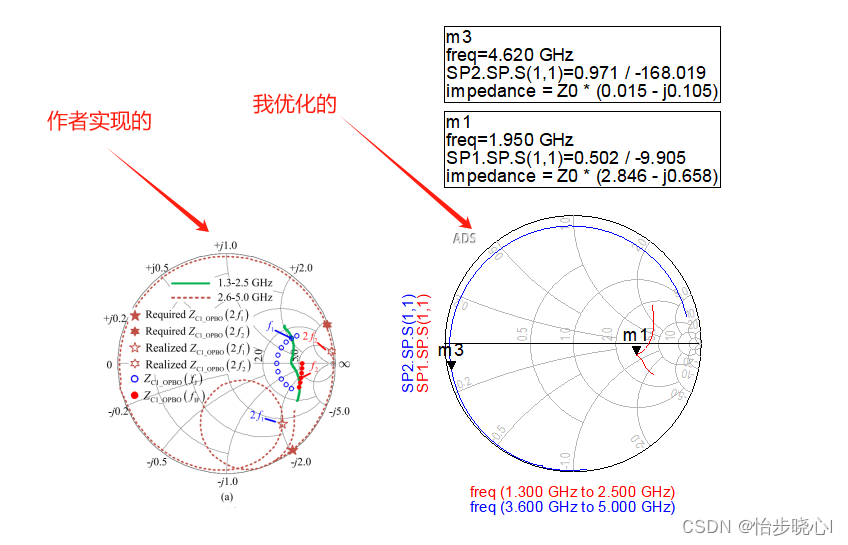
在这里插入图片描述

在这里插入图片描述

3.3 输入匹配设计

两个管子分别是13W的CGH40010F和25W的CGH40025F，基本上在频段内要匹配到10欧姆附近（源牵引得到），如CGH40025F在1.9GHz的源牵引数据：
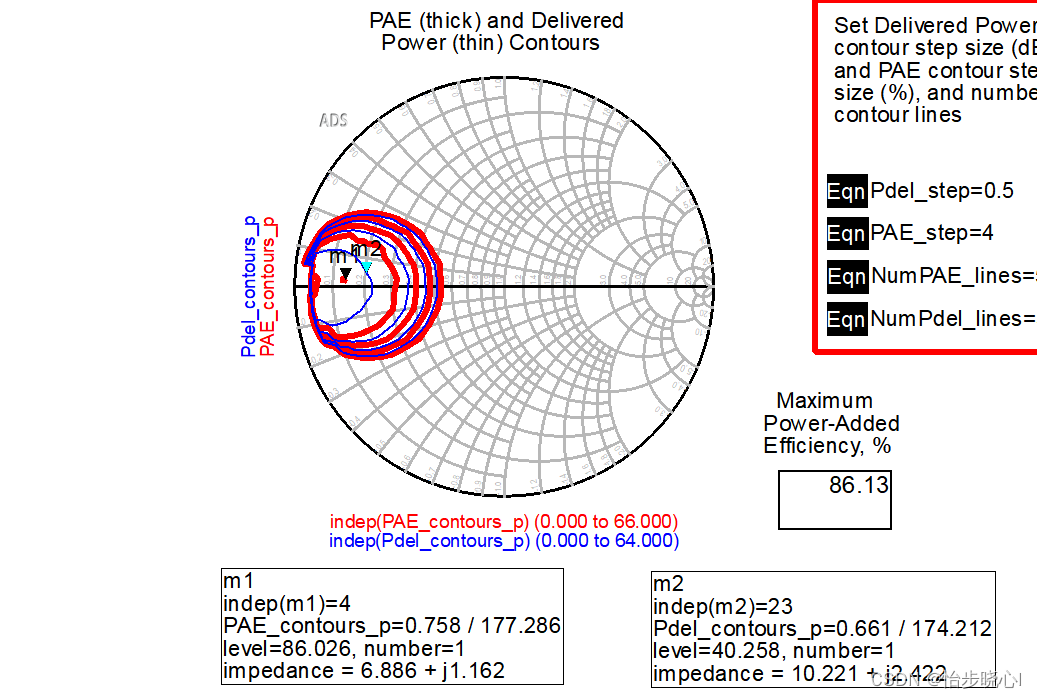
在这里插入图片描述
匹配电路的原理图、版图、测试在InputMatch文件夹，效果还可以：

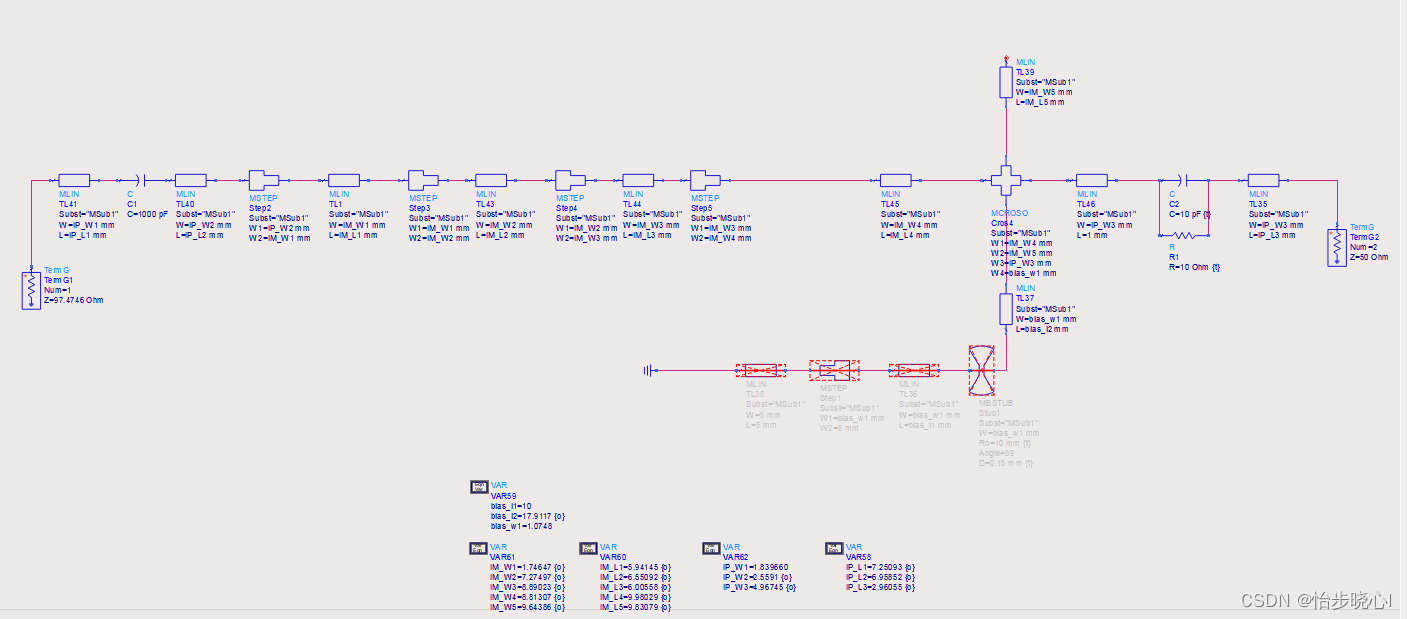
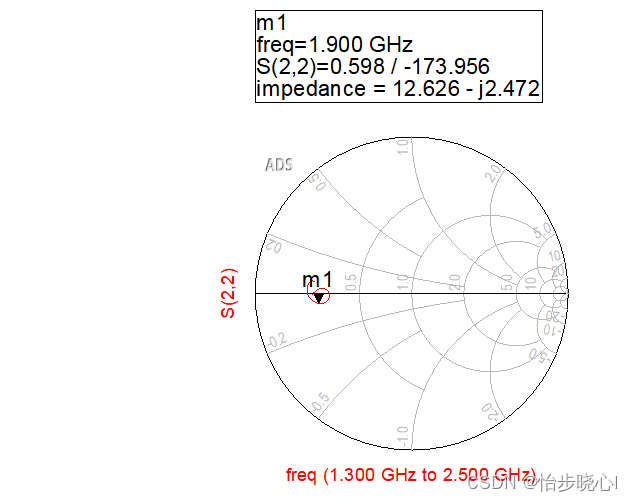
在这里插入图片描述

3.4 整体的仿真

为了方便调整功分比，我直接使用两个端口来输入（HB1ToneGComp1swp_Doherty_v1原理图，载波功放和峰值功放分开，方便调整功率分配比alpha）：

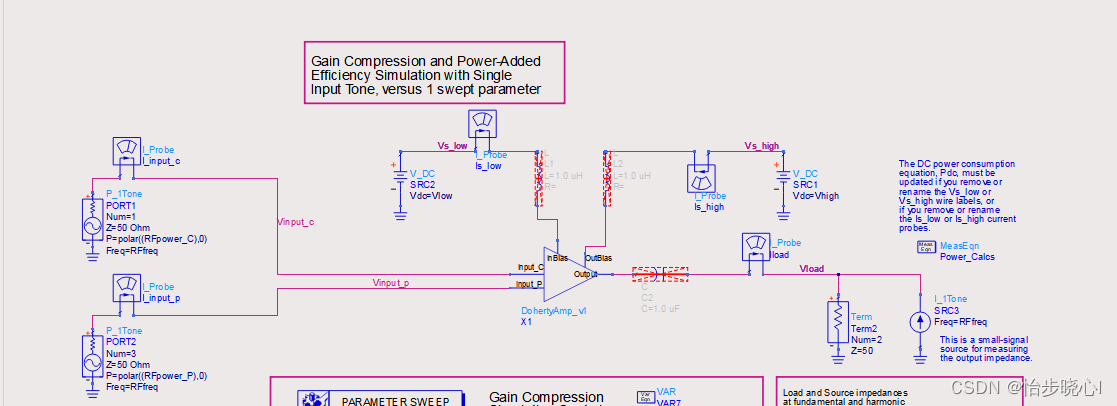
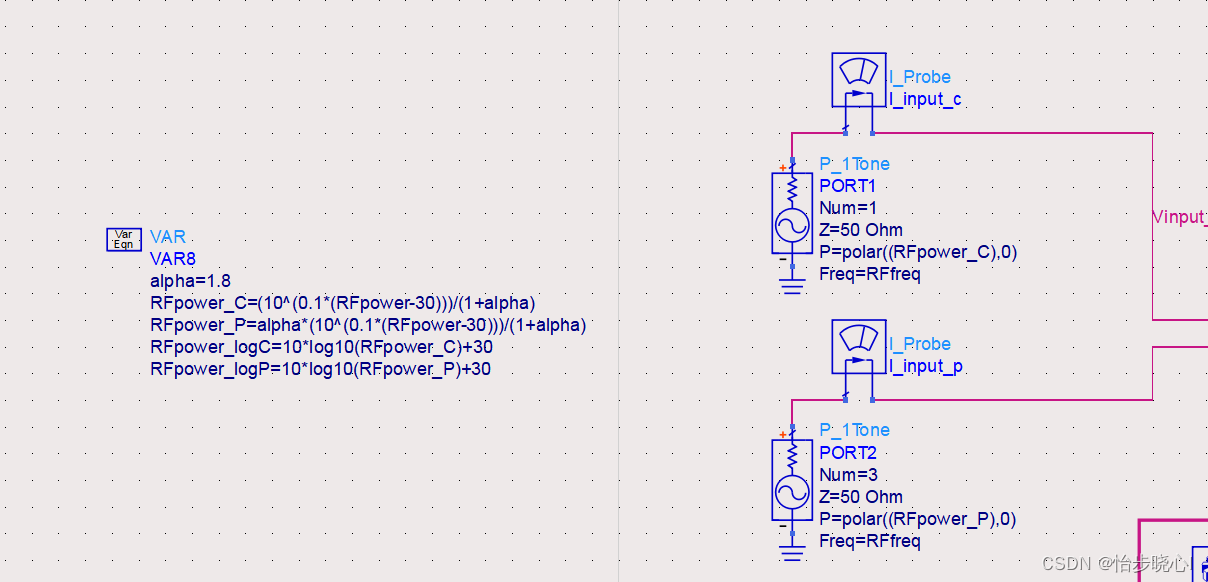
在这里插入图片描述

运行仿真，效果捉急（1.6-2.3GHz，9dB回退效率也能到50%左右吧，峰值效率60%左右）：
在这里插入图片描述
只能复现到这儿了，卡住了，效果有点垃，不知道哪儿有问题。

4 测试运行

运行Test中的HB1ToneGComp1swp_Doherty_v1即可，需要添加Cree公式的GAN的库路径。

附录

Case3的电长度计算：

close all
clear
clc
global ZC2_OPBO ZC1_OPBP_f0 ZTCOPBO=9;K=10^(OPBO/-20);% EQN1
alpha=1/K-1;% EQN2
% 单位化Ropt
Ropt=1;
% 归一化化频率
f0=1;
% ZTC使用作者设定的
ZTC=2.3*Ropt;
% %% Case1
% ZTP=Ropt;
% f_arrary_J=f0*0.7:0.1:f0*1.3;
% ZOF=ZTC*ZTP/Ropt;% EQN3
% Zpmn=K*ZTC*ZTC/Ropt;% EQN4
% ZC1_OPBP_f0=Ropt/K;% EQN5
% theta_TP=90*f_arrary_J/f0+1e-9;% theta_TP在中心频率处是90°
% theta_OF=90*f_arrary_J/f0+1e-9;% theta_OF在中心频率处是90°
% ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
% ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
% ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17
% 
% theta_TC_tmp=[40 50 60 90 120 130 140]+1e-12;
% A=[];b=[];Aeq=[];beq=[];
% lb=zeros(1,length(ZP2_OPBO));ub=180*ones(1,length(ZP2_OPBO));
% 
% theta_TC_J = fmincon(@theta_TC_cal_J,theta_TC_tmp,A,b,Aeq,beq,lb,ub);
% 
% ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_J))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_J));
% % 绘图
% S_ZC2_OPBO=(ZC2_OPBO-1)./(ZC2_OPBO+1);
% S_ZC1_OPBO=(ZC1_OPBO-1)./(ZC1_OPBO+1);
% figure(1)
% subplot(1,2,1)
% s = smithplot(S_ZC2_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
% hold on
% s = smithplot(S_ZC1_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
% s.Marker = {'s','o'};
% legend('Z_{C2\_OPBO}','Z_{C1\_OPBO}')
% 
% subplot(1,2,2)
% subplot(1,2,2)
% plot(f_arrary_J,-theta_TC_J);
% legend('\theta_J')
% xlabel('Normalized Frequency')
% ylabel('Required Phase(°)')
% %% Case2
% % J
% ZTP=0.2*Ropt;
% f_arrary_J=f0*0.9:0.03:f0*1.1;
% ZOF=ZTC*ZTP/Ropt;% EQN3
% Zpmn=K*ZTC*ZTC/Ropt;% EQN4
% ZC1_OPBP_f0=Ropt/K;% EQN5
% theta_TP=90*f_arrary_J/f0+1e-9;% theta_TP在中心频率处是90°
% theta_OF=90*f_arrary_J/f0+1e-9;% theta_OF在中心频率处是90°
% ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
% ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
% ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17
% 
% theta_TC_tmp=[40 50 60 90 120 130 140]+1e-12;
% A=[];b=[];Aeq=[];beq=[];
% lb=zeros(1,length(ZP2_OPBO));ub=180*ones(1,length(ZP2_OPBO));
% 
% theta_TC_J = fmincon('theta_TC_cal_J',theta_TC_tmp,A,b,Aeq,beq,lb,ub);
% 
% 
% ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_J))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_J));
% S_ZC2_OPBO=(ZC2_OPBO-1)./(ZC2_OPBO+1);
% S_ZC1_OPBO=(ZC1_OPBO-1)./(ZC1_OPBO+1);
% figure(2)
% subplot(1,2,1)
% s = smithplot(S_ZC2_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
% hold on
% s = smithplot(S_ZC1_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
% hold on
% 
% % IF
% 
% f_arrary_IF=f0*linspace(1.09, 1.11, 7);
% theta_TP=90*f_arrary_IF/f0+1e-9;% theta_TP在中心频率处是90°
% theta_OF=90*f_arrary_IF/f0+1e-9;% theta_OF在中心频率处是90°
% ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
% ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
% ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17
% 
% ZIF_1_f0=ZC1_OPBP_f0*2;% EQN12
% theta_TC_tmp=[120 120 120 120 120 120 120]+1e-12;
% A=[];b=[];Aeq=[];beq=[];
% theta_TC_IF = fmincon('theta_TC_cal_IF',theta_TC_tmp,A,b,Aeq,beq,lb,ub);
% 
% ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_IF))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_IF));
% S_ZC2_OPBO=(ZC2_OPBO-1)./(ZC2_OPBO+1);
% S_ZC1_OPBO=(ZC1_OPBO-1)./(ZC1_OPBO+1);
% 
% s = smithplot(S_ZC2_OPBO,'Color','r','LineStyle','-.','LineWidth',1);
% hold on
% s = smithplot(S_ZC1_OPBO,'Color','r','LineStyle','-.','LineWidth',1);
% s.Marker = {'s','o','s','o'};
% legend('J-Z_{C2\_OPBO}','J-Z_{C1\_OPBO}','IF-Z_{C2\_OPBO}','IF-Z_{C1\_OPBO}')
% 
% subplot(1,2,2)
% plot(f_arrary_J,-theta_TC_J);
% hold on
% plot(f_arrary_IF,-theta_TC_IF);
% legend('\theta_J','\theta_IF')
% xlabel('Normalized Frequency')
% ylabel('Required Phase(°)')
%% Case3
% J
ZTP=0.67*Ropt;
f_arrary_J=f0*linspace(0.7, 1.24, 7);
ZOF=ZTC*ZTP/Ropt;% EQN3
Zpmn=K*ZTC*ZTC/Ropt;% EQN4
ZC1_OPBP_f0=Ropt/K;% EQN5
theta_TP=90*f_arrary_J/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_J/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17theta_TC_tmp=[40 50 60 90 120 130 140]+1e-12;
A=[];b=[];Aeq=[];beq=[];
lb=zeros(1,length(ZP2_OPBO));ub=180*ones(1,length(ZP2_OPBO));theta_TC_J = fmincon('theta_TC_cal_J',theta_TC_tmp,A,b,Aeq,beq,lb,ub);ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_J))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_J));
S_ZC2_OPBO=(ZC2_OPBO-1)./(ZC2_OPBO+1);
S_ZC1_OPBO=(ZC1_OPBO-1)./(ZC1_OPBO+1);
figure(3)
subplot(1,2,1)
s = smithplot(S_ZC2_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
hold on
s = smithplot(S_ZC1_OPBO,'Color','b','LineStyle','-.','LineWidth',1);
hold on% IFf_arrary_IF=f0*linspace(1.25, 1.3, 7);
theta_TP=90*f_arrary_IF/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_IF/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17ZIF_1_f0=ZC1_OPBP_f0*2;% EQN12
theta_TC_tmp=[120 120 120 120 120 120 120]+1e-12;
A=[];b=[];Aeq=[];beq=[];
theta_TC_IF = fmincon('theta_TC_cal_IF',theta_TC_tmp,A,b,Aeq,beq,lb,ub);ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_IF))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_IF));
S_ZC2_OPBO=(ZC2_OPBO-1)./(ZC2_OPBO+1);
S_ZC1_OPBO=(ZC1_OPBO-1)./(ZC1_OPBO+1);s = smithplot(S_ZC2_OPBO,'Color','r','LineStyle','-.','LineWidth',1);
hold on
s = smithplot(S_ZC1_OPBO,'Color','r','LineStyle','-.','LineWidth',1);
s.Marker = {'s','o','s','o'};
legend('J-Z_{C2\_OPBO}','J-Z_{C1\_OPBO}','IF-Z_{C2\_OPBO}','IF-Z_{C1\_OPBO}')subplot(1,2,2)
plot(f_arrary_J,-theta_TC_J);
hold on
plot(f_arrary_IF,-theta_TC_IF);
legend('\theta_J','\theta_IF')
xlabel('Normalized Frequency')
ylabel('Required Phase(°)')

效率计算：

close all
clear
clc
global ZC2_OPBO ZC1_OPBP_f0 ZTCOPBO=9;K=10^(OPBO/-20);% EQN1
alpha=1/K-1;% EQN2
% 单位化Ropt
Ropt=25;
Ic_max=1;
Ip_max=alpha*Ic_max;
VDD=0.5*Ropt*Ic_max;
% 归一化化频率
f0=1;
% ZTC使用作者设定的
ZTC=2.3*Ropt;%% Case3 饱和计算
% J
ZTP=0.67*Ropt;
f_arrary_size=80;
f_arrary_J=f0*linspace(0.7, 1.24, f_arrary_size);
ZOF=ZTC*ZTP/Ropt;% EQN3
Zpmn=K*ZTC*ZTC/Ropt;% EQN4
theta=90*f_arrary_J;% 饱和状态计算，峰值功放负载确定
Ropt_P=Ropt/alpha;
Zp2=ZTP*(Ropt_P+1j*ZTP*tand(theta))./(ZTP+1j*Ropt_P*tand(theta));
Zp1=ZOF*(Zp2+1j*ZOF*tand(theta))./(ZOF+1j*Zp2.*tand(theta));
Zc2=1./(1/Zpmn-1./Zp1);ZC1_OPBP_f0=Ropt/K;% EQN5
theta_TP=90*f_arrary_J/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_J/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17theta_TC_tmp1=40*ones(1,(f_arrary_size)/2);
theta_TC_tmp2=140*ones(1,(f_arrary_size)/2);
theta_TC_tmp=[theta_TC_tmp1 theta_TC_tmp2];
clear theta_TC_tmp1 theta_TC_tmp2
A=[];b=[];Aeq=[];beq=[];nonlcon=[];
lb=zeros(1,length(ZP2_OPBO));ub=180*ones(1,length(ZP2_OPBO));options = optimoptions('fmincon','MaxFunctionEvaluations',60000);
theta_TC_J = fmincon('theta_TC_cal_J',theta_TC_tmp,A,b,Aeq,beq,lb,ub,nonlcon,options);
Zc1_J=ZTC*(Zc2+1j*ZTC*tand(theta_TC_J))./(ZTC+1j*Zc2.*tand(theta_TC_J));
% abs(Zc1_J)
% POUT_C=1/8*Ic_max*Ropt;
POUT_C=0.5*VDD*VDD./(abs(Zc1_J).*abs(Zc1_J)./real(Zc1_J));POUT_P=0.25*Ip_max*VDD;
Pdc=1/pi*VDD*(Ic_max+Ip_max);
eta_J=(POUT_C+POUT_P)/Pdc;f_arrary_IF=f0*linspace(1.25, 1.3, f_arrary_size);
theta_TP=90*f_arrary_IF/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_IF/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17ZIF_1_f0=ZC1_OPBP_f0*2;% EQN12
theta_TC_tmp=120*ones(1,f_arrary_size);
A=[];b=[];Aeq=[];beq=[];nonlcon=[];
options = optimoptions('fmincon','MaxFunctionEvaluations',60000);
theta_TC_IF = fmincon('theta_TC_cal_IF',theta_TC_tmp,A,b,Aeq,beq,lb,ub,nonlcon,options);
Zc1_F=ZTC*(Zc2+1j*ZTC*tand(theta_TC_IF))./(ZTC+1j*Zc2.*tand(theta_TC_IF));% POUT_C=1/8*Ic_max*Ropt;
POUT_C=0.5*VDD*VDD./(abs(Zc1_F).*abs(Zc1_F)./real(Zc1_F));
POUT_P=0.25*Ip_max*VDD;
Pdc=1/pi*VDD*(Ic_max+Ip_max);
eta_F=(POUT_C+POUT_P)/Pdc;plot([f_arrary_J f_arrary_IF],[eta_J eta_F])
xlabel('Normalized Frequency')
ylabel('Drain Efficiency(%)')
title('Efficiency')

ZPMN谐波阻抗计算：

close all
clear
clc
global ZC2_OPBO ZC1_OPBP_f0 ZTCOPBO=11;K=10^(OPBO/-20);% EQN1
alpha=1/K-1;% EQN2
% 单位化Ropt
Ropt=1;
Ic_max=1;
Ip_max=alpha*Ic_max;
VDD=0.5*Ropt*Ic_max;
% 归一化化频率
f0=1;
% ZTC使用作者设定的
ZTC=2.3*Ropt;%% Case3 饱和计算
% J
ZTP=0.67*Ropt;
f_arrary_size=12;
f_arrary_J=f0*linspace(0.7, 1.24, f_arrary_size);
ZOF=ZTC*ZTP/Ropt;% EQN3
Zpmn=K*ZTC*ZTC/Ropt;% EQN4
theta=90*f_arrary_J;ZC1_OPBP_f0=Ropt/K;% EQN5
theta_TP=90*f_arrary_J/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_J/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17theta_TC_tmp1=40*ones(1,(f_arrary_size)/2);
theta_TC_tmp2=140*ones(1,(f_arrary_size)/2);
theta_TC_tmp=[theta_TC_tmp1 theta_TC_tmp2];
clear theta_TC_tmp1 theta_TC_tmp2
A=[];b=[];Aeq=[];beq=[];nonlcon=[];
lb=zeros(1,length(ZP2_OPBO));ub=180*ones(1,length(ZP2_OPBO));options = optimoptions('fmincon','MaxFunctionEvaluations',60000);
theta_TC_J = fmincon('theta_TC_cal_J',theta_TC_tmp,A,b,Aeq,beq,lb,ub,nonlcon,options);ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_J))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_J));
figure
plot(f_arrary_J,theta_TC_J)
ZC1_OPBO_2f=-1j*imag(ZC1_OPBO)*3*pi/8;
ZC2_OPBO_2f=ZTC*(ZC1_OPBO_2f-1j*ZTC*tand(2*theta_TC_J))./(ZTC-1j*ZC1_OPBO_2f.*tand(2*theta_TC_J));
Zpmn_2f_J=ZC2_OPBO_2f.*ZP1_OPBO./(ZP1_OPBO-ZC2_OPBO_2f);ZC1_OPBO_3f=1e99;
ZC2_OPBO_3f=ZTC*(ZC1_OPBO_3f-1j*ZTC*tand(3*theta_TC_J))./(ZTC-1j*ZC1_OPBO_3f.*tand(3*theta_TC_J));
Zpmn_3f_J=ZC2_OPBO_3f.*ZP1_OPBO./(ZP1_OPBO-ZC2_OPBO_3f);f_arrary_IF=f0*linspace(1.25, 1.3, f_arrary_size);
theta_TP=90*f_arrary_IF/f0+1e-9;% theta_TP在中心频率处是90°
theta_OF=90*f_arrary_IF/f0+1e-9;% theta_OF在中心频率处是90°
ZP2_OPBO=ZTP./(1j*tand(theta_TP));% EQN15
ZP1_OPBO=ZOF.*(ZP2_OPBO+1j*ZOF.*tand(theta_OF))./(ZOF+1j*ZP2_OPBO.*tand(theta_OF));% EQN16
ZC2_OPBO=ZP1_OPBO.*Zpmn./(ZP1_OPBO+Zpmn);% EQN17ZIF_1_f0=ZC1_OPBP_f0*2;% EQN12
theta_TC_tmp=120*ones(1,f_arrary_size);
A=[];b=[];Aeq=[];beq=[];nonlcon=[];
options = optimoptions('fmincon','MaxFunctionEvaluations',60000);
theta_TC_IF = fmincon('theta_TC_cal_IF',theta_TC_tmp,A,b,Aeq,beq,lb,ub,nonlcon,options);ZC1_OPBO=ZTC.*(ZC2_OPBO+1j*ZTC.*tand(theta_TC_IF))./(ZTC+1j*ZC2_OPBO.*tand(theta_TC_IF));gamma=real((ZIF_1_f0/1.644-0.43*sqrt(2)*ZC1_OPBO)./(1j*0.37*sqrt(2)*ZC1_OPBO));
ZC1_OPBO_2f=(1j*ZIF_1_f0/1.644)./(0.98*gamma);
ZC2_OPBO_2f=ZTC*(ZC1_OPBO_2f-1j*ZTC*tand(2*theta_TC_IF))./(ZTC-1j*ZC1_OPBO_2f.*tand(2*theta_TC_IF));
Zpmn_2f_IF=ZC2_OPBO_2f.*ZP1_OPBO./(ZP1_OPBO-ZC2_OPBO_2f);figure
plot(f_arrary_IF,theta_TC_IF)% % S_Zpmn_2f_J=(Zpmn_2f_J-1)./(Zpmn_2f_J+1);
% % s = smithplot(S_Zpmn_2f_J,'Color','r','LineStyle','-.','LineWidth',1);
% % 
% % S_Zpmn_2f_IF=(Zpmn_2f_IF-1)./(Zpmn_2f_IF+1);
% % hold on
% % s = smithplot(S_Zpmn_2f_IF,'Color','r','LineStyle','-.','LineWidth',1);